本文介绍了 LSTM (长短时记忆网络)的基本概念,以及正/反向传播的推导过程,然后分析了 LSTM 如何克服 RNN 的梯度消失问题,最后介绍了 PyTorch 的 LSTM 模块的实现。
1. LSTM
1.1. 概念
长短期记忆(Long short-term memory, LSTM)是一种特殊的RNN(Gers et al.,2000; Hochreiter et al., 1997),主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。
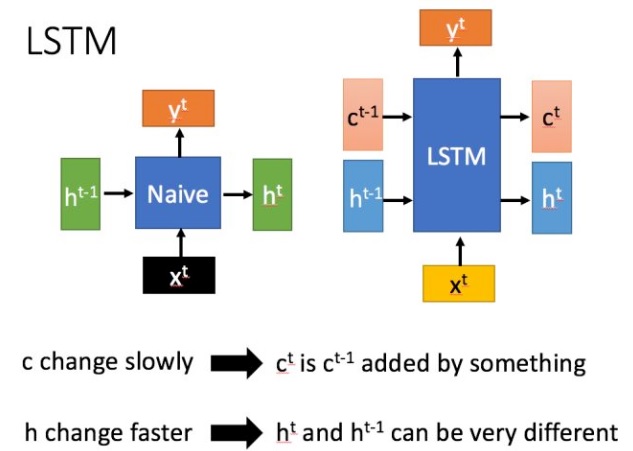
LSTM 与 RNN 的主要输入输出区别如下图所示
1.2. 模型
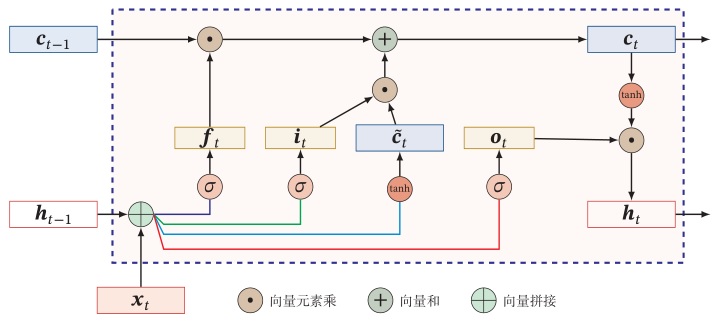
LSTM 网络的循环单元结构如下图所示
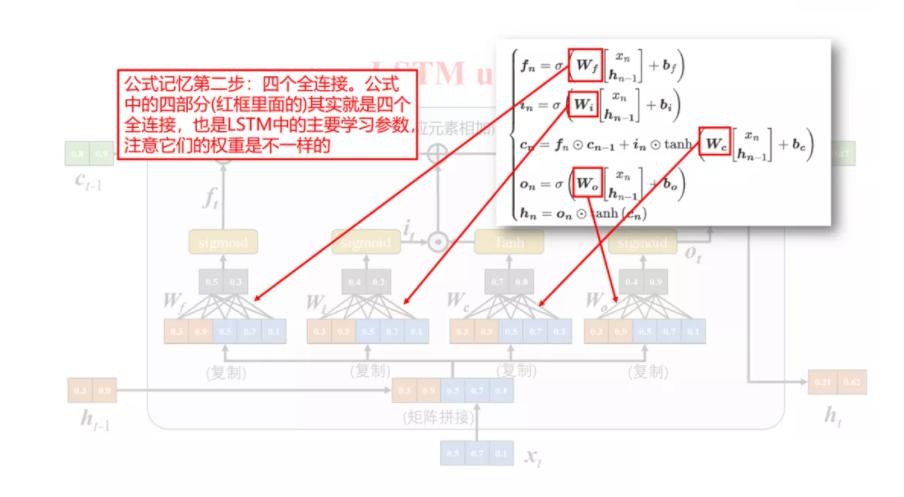
其中,LSTM 引入三个门来控制信息的传递,分别为遗忘门 $\boldsymbol{f}_t$、输入门 $\boldsymbol{i}_t$、输出门 $\boldsymbol{o}_t$。三个门的作用是:
- 遗忘门 $\boldsymbol{f}t$ 控制上一个时刻的内部状态 $\boldsymbol{c}{t-1}$ 需要遗忘多少信息;
- 输入门 $\boldsymbol{i}_t$ 控制当前时刻的候选状态 $\boldsymbol{c}_t$ 有多少信息需要保存;
- 输出门 $\boldsymbol{o}_t$ 控制当前时刻的内部状态 $\boldsymbol{c}_t$ 有多少信息需要输出给外部状态 $\boldsymbol{h}_t$。
1.3. 前向传播
三个门的计算方式为:
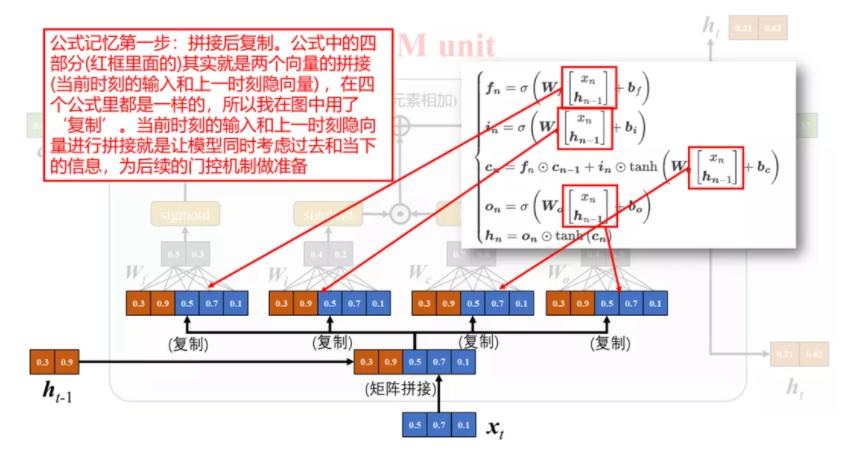
\[\begin{aligned} \boldsymbol{f}_t &= \sigma(\boldsymbol W_f \boldsymbol{h}_{t-1} + \boldsymbol{U}_f \boldsymbol{x}_t + \boldsymbol{b}_f)=\sigma([\boldsymbol W_f, \boldsymbol{U}_f]\cdot[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t]^T + \boldsymbol{b}_f)\\ \boldsymbol{i}_t &= \sigma(\boldsymbol W_i \boldsymbol{h}_{t-1} + \boldsymbol{U}_i \boldsymbol{x}_t + \boldsymbol{b}_i)=\sigma([\boldsymbol W_i, \boldsymbol{U}_i]\cdot[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t]^T + \boldsymbol{b}_f)\\ \boldsymbol{o}_t &= \sigma(\boldsymbol W_o \boldsymbol{h}_{t-1} + \boldsymbol{U}_o \boldsymbol{x}_t + \boldsymbol{b}_o)=\sigma([\boldsymbol W_o, \boldsymbol{U}_o]\cdot[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t]^T + \boldsymbol{b}_f)\\ \end{aligned}\]其中,$\sigma$ 为 $sigmoid$ 激活函数,输出区间为 $[0,1]$。也就是说,LSTM 网络中的“门”是一种“软”门,取值在 $[0,1]$ 之间,表示以一定的比例允许信息通过。注意到,等式右边包含一个对 $\boldsymbol{h}_{t-1}$ 和 $\boldsymbol{x}_t$ 向量拼接的操作,相应的参数也因此进行了拼接。
相比 RNN,LSTM 引入了一个新的状态,称为细胞状态(cell state),表示为 $\boldsymbol{c}_t$,专门进行现行的循环信息传递,同时输出(非线性地)输出信息给隐层状态 $\boldsymbol{h}_t\in \mathbb{R}^D$。计算公式如下
\[\begin{aligned} \boldsymbol{c}_t &= \tanh(\boldsymbol W_c \boldsymbol{h}_{t-1} + \boldsymbol{U}_c \boldsymbol{x}_t + \boldsymbol{b}_c)=\tanh([\boldsymbol W_c, \boldsymbol{U}_c]\cdot[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t]^T + \boldsymbol{b}_f)\\ \boldsymbol{c}_t &= \boldsymbol{f}_t \odot \boldsymbol{c}_{t-1} + \boldsymbol{i}_t \odot \boldsymbol{c}_t\\ \boldsymbol{h}_t &= \boldsymbol{o}_t \odot \tanh(\boldsymbol{c}_t) \end{aligned}\]其中,
- $\boldsymbol{c}_t\in\mathbb{R}^D$ 是通过非线性函数($\tanh$)得到的候选状态,
- $\boldsymbol{c}_{t-1}$ 是上一时刻的记忆单元,
- $\odot$ 是向量的元素乘积。
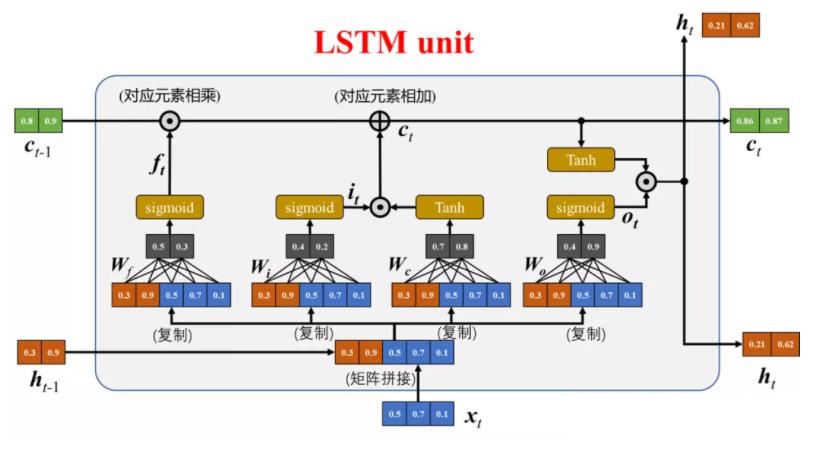
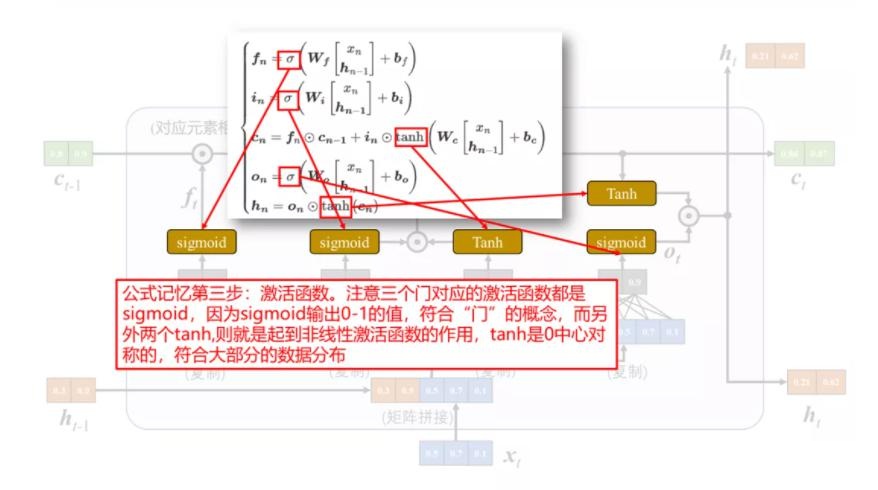
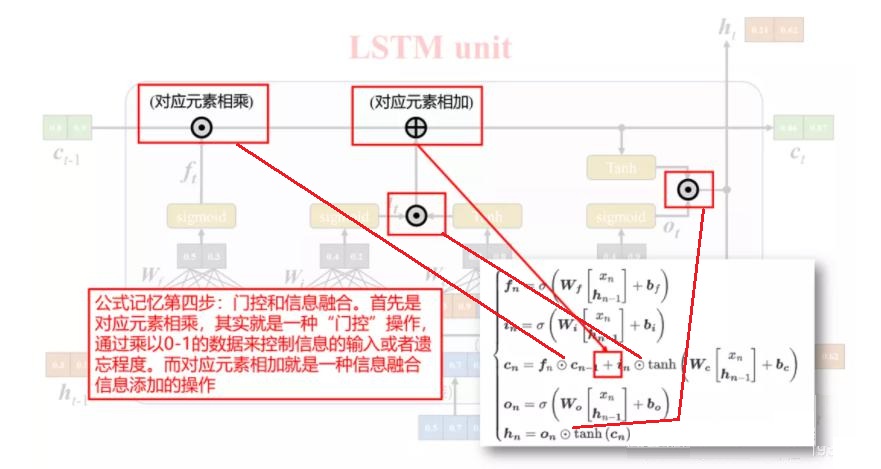
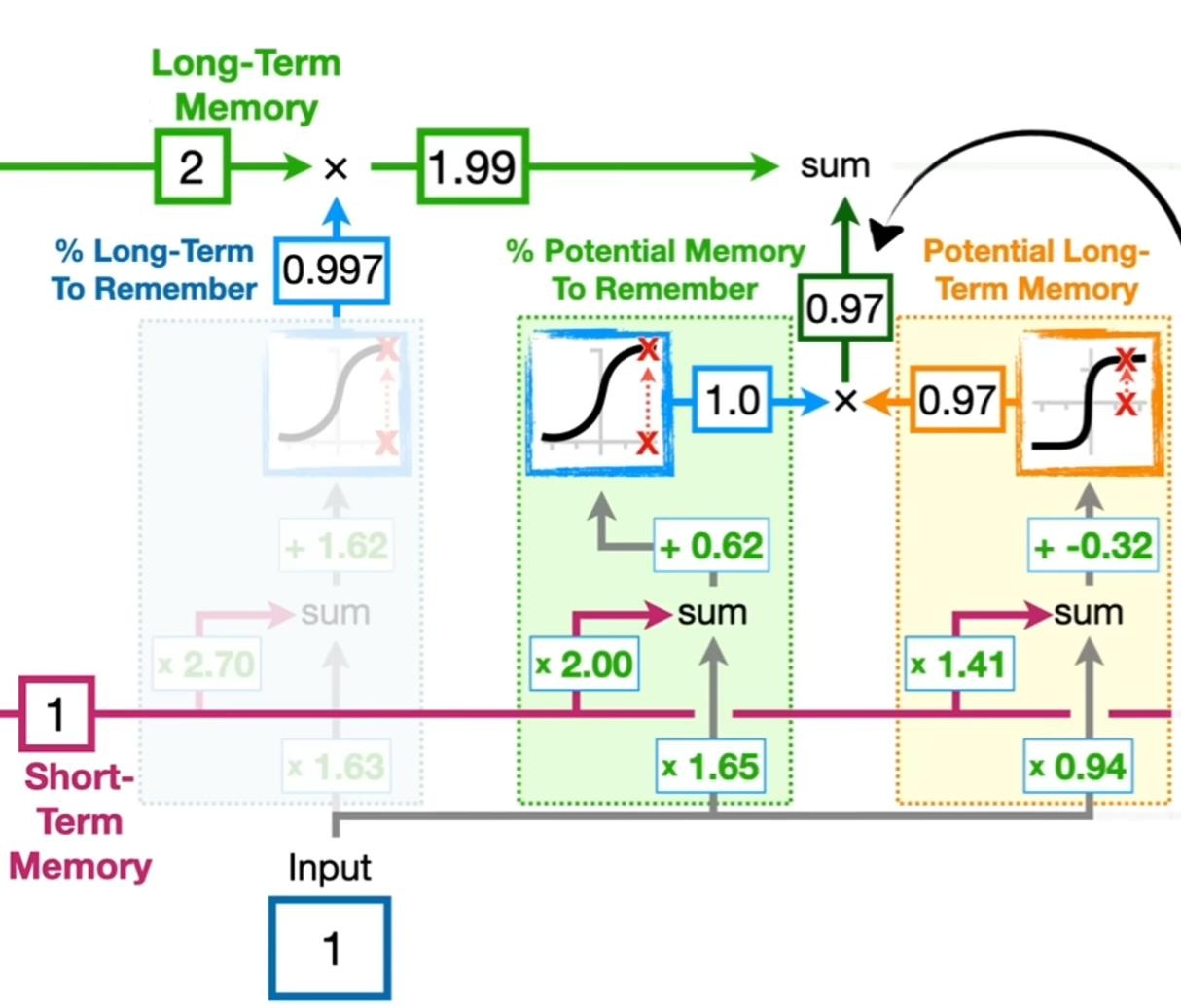
下面是将 LSTM 组成部分和计算公式的对应关系绘制成图[3]:
最后,对公式进行进一步简化,令,$\boldsymbol{h}_t,\boldsymbol{c}_t,\boldsymbol{i}_t,\boldsymbol{f}_t,\boldsymbol{o}_t \in \mathbb R^D$ 且 $\boldsymbol{b}_f,\boldsymbol{b}_i,\boldsymbol{b}_o,\boldsymbol{b}_c \in \mathbb R^D$,$\boldsymbol{x}_t\in \mathbb R^M$,那么 $\boldsymbol W_f,\boldsymbol W_i,\boldsymbol W_o,\boldsymbol W_c \in \mathbb R^{D\times M}$, $\boldsymbol{U}_f,\boldsymbol{U}_i,\boldsymbol{U}_o,\boldsymbol{U}_c \in \mathbb R^{D\times D}$。则上面所有式子可简洁描述为
\[\begin{aligned} \begin{bmatrix} \boldsymbol{c}_t\\ \boldsymbol{o}_t\\ \boldsymbol{i}_t\\ \boldsymbol{f}_t \end{bmatrix}= \begin{bmatrix} \tanh\\ \sigma\\ \sigma\\ \sigma \end{bmatrix}\left( \boldsymbol W \begin{bmatrix} \boldsymbol{h}_{t-1}\\ \boldsymbol{x}_t \end{bmatrix}+\boldsymbol b \right) \end{aligned}\]其中
\[\begin{aligned} \boldsymbol W &=\begin{bmatrix} \boldsymbol W_c & \boldsymbol{U}_c\\ \boldsymbol W_o & \boldsymbol{U}_o\\ \boldsymbol W_i & \boldsymbol{U}_i\\ \boldsymbol W_f & \boldsymbol{U}_f \end{bmatrix} \in \mathbb R^{4D\times (D+M)}\\ \boldsymbol b &= \begin{bmatrix} \boldsymbol{b}_c\\ \boldsymbol{b}_o\\ \boldsymbol{b}_i\\ \boldsymbol{b}_f \end{bmatrix}\in \mathbb R^{4D} \end{aligned}\]在每个时刻,LSTM 网络的细胞状态 $\boldsymbol{c}_t$ 记录了截至当前时刻的历史信息,对应于传统 RNN 中的 $\boldsymbol{h}_t$,通常是上一个传过来的历史状态乘以遗忘门后加上一些新信息得到,因此更新比较缓慢。而 LSTM 中的 $\boldsymbol{h}_t$ 则变化剧烈的多,在不同的时刻下的取值往往区别很大。
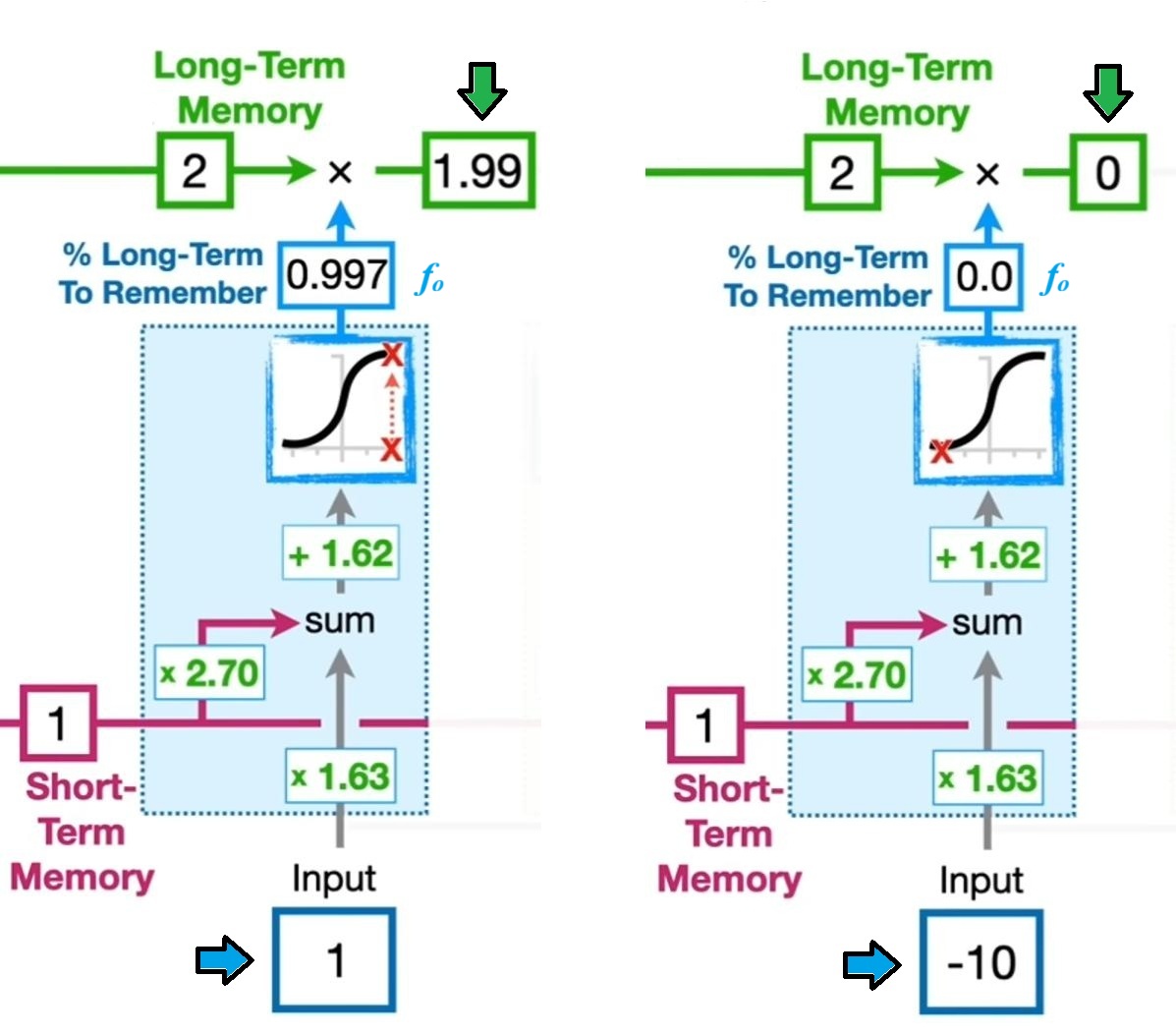
下面是当遗忘门的权重和偏置保持不变时,不同的输入对最终遗忘门的输出的影响[4]:
随后,观察后续两个模块的功能,其中右边黄色部分计算出了潜在的长期记忆的具体取值,而中间绿色部分为记忆门,其给出了到底多少比例的长期记忆需要被添加到最终的长期记忆中。代入数值后计算,可得有 $0.97$ 的潜在长期记忆被保留[4]:
根据不同的门状态取值,可以实现不同的功能。当 $\boldsymbol{f}_t = 0,\boldsymbol{i}_t = 1$ 时,记忆单元将历史信息清空,并将候选状态向量 $\boldsymbol{c}_t$ 写入,但此时记忆单元 $\boldsymbol{c}_t$ 依然和上一时刻的历史信息相关。当$\boldsymbol{f}_t = 1,\boldsymbol{i}_t = 0$ 时,记忆单元将复制上一时刻的内容,不写入新的信息。
最后两个模块是根据输出门来计算有多少新的长期记忆得到保留,以计算新的短期记忆:
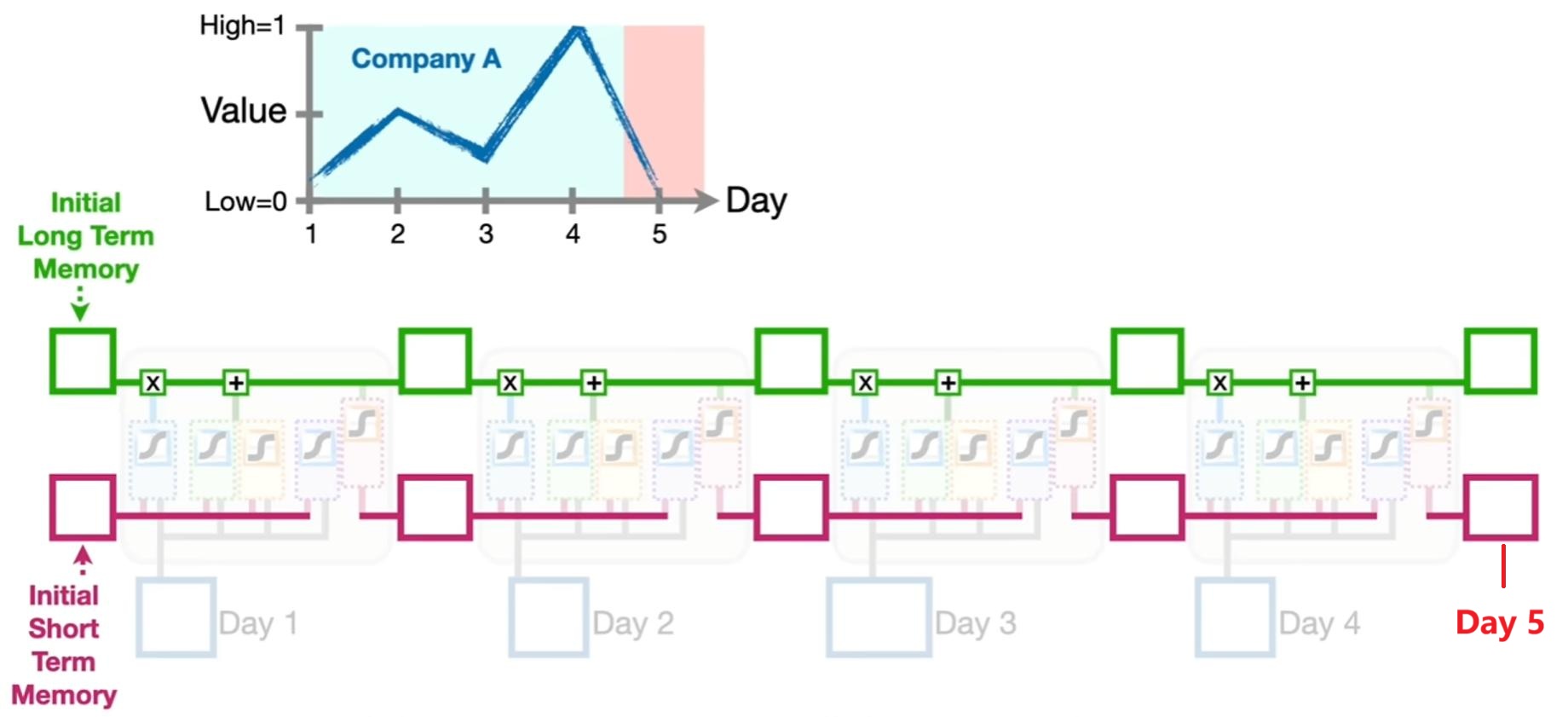
当我们使用 LSTM 时,一般输入的信息是一个时序序列,如根据公司的前四天的历史股价去预测未来一天的股价高低,如下图所示:
循环神经网络中的隐状态 $\boldsymbol h$ 存储了历史信息,可以看作一种记忆(Memory)。在简单循环网络中,隐状态每个时刻都会被重写,因此可以看作一种短期记忆(Short-Term Memory)。在神经网络中,长期记忆(Long-Term Memory)可以看作网络参数,隐含了从训练数据中学到的经验,其更新周期要远远慢于短期记忆。
而在 LSTM 网络中,记忆单元 $\boldsymbol c$ 可以在某个时刻捕捉到某个关键信息,并有能力将此关键信息保存一定的时间间隔。记忆单元 $\boldsymbol c$ 中保存信息的生命周期要长于短期记忆 $\boldsymbol h$,但又远远短于长期记忆,长短期记忆是指长的“短期记忆”。因此称为长短期记忆(Long Short-Term Memory)。
1.4. 如何解决梯度消失
LSTM 通过引入门机制,把矩阵乘法变成了 element-wise 的 Hadamard product(哈达玛积,逐元素相乘)。这样做后,细胞状态 $\boldsymbol{c}_t$ (对应于 RNN 中的隐状态 $\boldsymbol{h}_t$)的更新公式变为
\[\boldsymbol{c}_t = \boldsymbol{f}_t \odot \boldsymbol{c}_{t-1} + \boldsymbol{i}_t \odot \tanh(\boldsymbol W_c \boldsymbol{h}_{t-1} + \boldsymbol{U}_c \boldsymbol{x}_t + \boldsymbol{b}_c)\]进一步推导
\[\begin{aligned} \frac{\partial \boldsymbol L}{\partial \boldsymbol{c}_{t-1}} &= \frac{\partial L}{\partial c_t}\frac{\partial c_t}{\partial c_{t-1}} = \frac{\partial L}{\partial c_t} \odot diag(f_t+\cdots) \end{aligned}\]公式里其余的项不重要,这里就用省略号代替了。可以看出当 $f_t=1$ 时,就算其余项很小,梯度仍然可以很好地传导到上一个时刻,此时即使层数较深也不会发生 Gradient Vanish 的问题;当 $f_t=0$ 时,即上一时刻的信号不影响到当前时刻,则此项也会为0。$f_t$ 在这里控制着梯度传导到上一时刻的衰减程度,与它 Forget Gate 的功能一致。
这样的方式本质上类似 Highway Network 或者 ResNet(残差连接),使得梯度的信息可以“贯穿”时间线,缓解梯度消散。
这里需要强调的是:LSTM不是让所有远距离的梯度值都不会消散,而是只让具有时序关键信息位置的梯度可以一直传递。另一方面,仅在 $c_t$ 通路上缓解了梯度消失问题,而在 $h_t$ 通路上梯度消失依然存在。
1.5. 如何解决梯度爆炸
关于梯度爆炸问题: $f_t$ 已经在 $[0,1]$ 范围之内了。而且梯度爆炸爆炸也是相对容易解决的问题,可以用梯度裁剪(gradient clipping)来解决:只要设定阈值,当提出梯度超过此阈值,就进行截取即可。
另一种解读参见 [1] 。
2. 实际案例
2.1. LSTM 的 PyTorch 类
官方文档链接在此(https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html )
1
CLASStorch.nn.LSTM(*args, **kwargs)
参数列表如下
-
input_size – The number of expected features in the input x
-
hidden_size – The number of features in the hidden state h
-
num_layers – Number of recurrent layers. E.g., setting
num_layers=2would mean stacking two LSTMs together to form a stacked LSTM, with the second LSTM taking in outputs of the first LSTM and computing the final results. Default: 1 -
bias – If False, then the layer does not use bias weights b_ih and b_hh. Default:
True -
batch_first – If
True, then the input and output tensors are provided as (batch, seq, feature). Default:False -
dropout – If non-zero, introduces a Dropout layer on the outputs of each LSTM layer except the last layer, with dropout probability equal to
dropout. Default: 0 -
bidirectional – If
True, becomes a bidirectional LSTM. Default:False
我们再次将 LSTM 的前向传播列写如下便于比对
\[\begin{aligned} \boldsymbol{f}_t &= \sigma(\boldsymbol W_f \boldsymbol{h}_{t-1} + \boldsymbol{U}_f \boldsymbol{x}_t + \boldsymbol{b}_f)\\ \boldsymbol{i}_t &= \sigma(\boldsymbol W_i \boldsymbol{h}_{t-1} + \boldsymbol{U}_i \boldsymbol{x}_t + \boldsymbol{b}_i)\\ \boldsymbol{o}_t &= \sigma(\boldsymbol W_o \boldsymbol{h}_{t-1} + \boldsymbol{U}_o \boldsymbol{x}_t + \boldsymbol{b}_o)\\ \boldsymbol{c}_t &= \tanh(\boldsymbol W_c \boldsymbol{h}_{t-1} + \boldsymbol{U}_c \boldsymbol{x}_t + \boldsymbol{b}_c)\\ \boldsymbol{c}_t &= \boldsymbol{f}_t \odot \boldsymbol{c}_{t-1} + \boldsymbol{i}_t \odot \boldsymbol{c}_t\\ \boldsymbol{h}_t &= \boldsymbol{o}_t \odot \tanh(\boldsymbol{c}_t) \end{aligned}\]前面我们已经假设,$\boldsymbol{h}_t,\boldsymbol{c}_t,\boldsymbol{i}_t,\boldsymbol{f}_t,\boldsymbol{o}_t \in \mathbb R^D$ 且 $\boldsymbol{b}_f,\boldsymbol{b}_i,\boldsymbol{b}_o,\boldsymbol{b}_c \in \mathbb R^D$,$\boldsymbol{x}_t\in \mathbb R^M$,那么 $\boldsymbol W_f,\boldsymbol W_i,\boldsymbol W_o,\boldsymbol W_c \in \mathbb R^{D\times M}$, $\boldsymbol{U}_f,\boldsymbol{U}_i,\boldsymbol{U}_o,\boldsymbol{U}_c \in \mathbb R^{D\times D}$。
input_size 就是输入层维度 $M$,比如某个词或者某张图的 embedding dim (特征维度)。
hidden_size 就是隐层 $h_t$ 的维度 $D$。
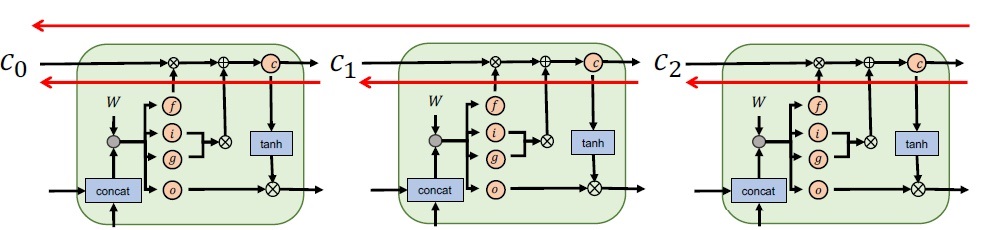
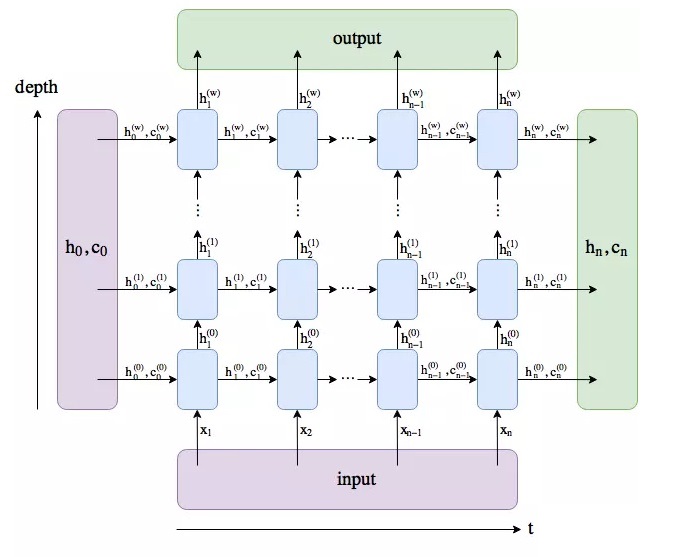
num_layers 是 LSTM 堆叠的层数。LSTM 可以按照下图的形式进行堆叠。
batch_first 是一个可选参数,指定是否将 batch_size 作为输入输出张量的第一个维度,如果是,则输入和输入的维度顺序为(batch_size, seq_length,input_size),否则,输入和输出的默认维度顺序是(seq_length, batch_size, input_size)。
2.2. LSTM 实现 MNIST 识别
注意,后文中的所有代码均为片段,全部凑在一起时无法直接运行的!旨在辅助进行理解。
考虑到网络每一时刻输入的是一个 vector,我们可以假设这个 vector 对应的是 图像的一行,有多少行就对应多少时刻,那最后一个时刻输入的是最后一行。最后输出的 $h_t$ 实际上就是该图像对应的类别。
MNIST 手写数字图片大小为 28*28,那么可以将每张图片看作长为28的序列,序列中的每个元素的特征维度是28,这样就将图片变成了一个序列。
那么有
1
2
3
4
5
input_size = 28 # image width
sequence_size = 28 # image height (time step)
hidden_size = 100 # user defined
output_size = 10 # 10 classes of number from 0 to 9
num_layers = 2 # user defined
其中 hidden_size 和 num_layers 均由用户自定义。
然后我们开始构建 LSTM 网络的类。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class MNIST_LSTM(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, output_dim):
super(MNIST_LSTM,self).__init__()
self.lstm = nn.LSTM(
input_size,
hidden_size,
num_layers,
batch_first=True)
# fully connect
self.fc = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# x - [batch_size, sequence_dim, input_dim]
# r_out - [batch_size, sequence_dim, hidden_size]
# h_n - [layer_dim, batch_size, hidden_size]
# h_c - [layer_dim, batch_size, hidden_size]
r_out, (h_n, h_c) = self.lstm(x, None)
# out - [batch_size, output_size]
out = self.fc(r_out[:,-1,:])
return out
在网络初始化时,我们引入了定义的 4 个形参 input_size, hidden_size, num_layers, output_size,确定网络的结构中的输入维度,隐层神经元个数,隐层层数,输出维度。
然后,按照上面定义的结构定义一个 torch 官方提供的 torch.nn.LSTM 单元,并且设定其 batch_first=True,即将数据的批数放到输入输出向量的第一个维度。
最后,定义一个全连接层,将隐层信息映射到输出维度。
在定义网络前向传播时,首先给 LSTM 传入输入向量 x 和 初始隐层向量 (h_n,h_c)。此处 x 维度为 [batch_size, sequence_size, input_size],初始隐层向量为 None,即表示初始时刻隐层向量均为 0 。
经过前向传播,LSTM 单元的输出为 r_out, (h_n, h_c)。其中
r_out也就是上面图中的 output 保存了最后一层,每个 time step 的输出h,如果是双向 LSTM,每个 time step 的输出h = [h正向, h逆向](同一个 time step 的正向和逆向的h连接起来)。- 所以
r_out无需层维度信息,而包含时间序列信息,其维度为[batch_size, sequence_size, output_size]; - 如果
num_layers=1,lstm 只有一层,则r_out为每个 time step 的输出。
- 所以
h_n保存了每一层,最后一个time step 的输出h,如果是双向LSTM,单独保存前向和后向的最后一个 time step 的输出 h。- 所以
h_n包含层维度信息,无需时间序列信息,其维度为[layer_size, batch_size, hidden_size];注意到batch_first=True不会影响到h_n,因此第一个维度是层个数; - 如果
num_layers=1,lstm 只有一层,则h_n为最后一个 time step 的输出。
- 所以
c_n与h_n一致,只是它保存的是c的值。
继续经过全连接层,输入 r_out 输出 out :
r_out[:,-1,:]表示读取r_out第二维的倒数第一个元素对应的其余维度数据。由于r_out的第二维是sequence_size也就是 time step,倒数第一个元素对应的其余维度数据也就是最后一个时刻的数据[batch_size, hidden_size];- 当
layer_size = 1时,r_out[:,-1,:] = h_n[-1,:,:]; - 经过全连接层,得到 batch 中每张图片的最终分类结果
[batch_size, output_size]。
最后设计训练和测试环节。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
def main():
root = "./mnist/MNIST/raw/"
train_mean = 0.1307
train_std = 0.3081
batch_size = 64
test_batch_size = 50
kwargs = {'num_workers': 2, 'pin_memory': True} if use_cuda else {}
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((train_mean,), (train_std,))
])
train_loader = torch.utils.data.DataLoader(
DATA(root, train=True, transform=transform),
batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
DATA(root, train=False, transform=transform),
batch_size=test_batch_size, shuffle=True, **kwargs)
model = MNIST_LSTM(input_size, hidden_size, layer_num, output_size)
if use_cuda:
model.to(device)
lossfcn = nn.CrossEntropyLoss()
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
loss_list = []
accuracy_list = []
iteration_list = []
EPOCHS = 20
iter = 0
for epoch in range(1,EPOCHS+1):
print("EPOCH: {}".format(epoch))
loss = 999.0
for batchidx, (images, labels) in enumerate(train_loader):
model.train()
# 一个batch 转换为RNN的输入维度
images = images.view(-1, sequence_size, input_size)
images = images.requires_grad_()
labels = labels.long() # cross entropy requires a long scalar
# 移入GPU
if use_cuda:
images, labels = images.to(device), labels.to(device)
# 梯度清零
optimizer.zero_grad()
# 前向传播
output = model(images)
# 计算损失
loss = lossfcn(output, labels)
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
iter += 1
# 打印训练信息
if batchidx % 50 == 0:
print("batch index: {}, images: {}/{}+[{}], loss: {}".format(
batchidx,
batchidx*batch_size,
train_loader.dataset.data.shape[0],batch_size,
loss.data.cpu().numpy()))
# 模型验证
model.eval()
correct = 0.0
total = 0.0
# 迭代测试集,获取数据,预测
with torch.no_grad():
for images, labels in test_loader:
images = images.view(-1, sequence_size, input_size).to(device)
# 模型预测
output = model(images)
# 获取预测概率最大值的下标
_, predict = torch.max(output.data, axis=1)
# 统计测试集的大小
total += labels.size(0)
# 统计预测正确的数量
if use_cuda:
predict, labels = predict.to(device), labels.to(device)
correct += (predict == labels).sum()
accuracy = correct / total * 100
# 保存accuracy,loss,iteration
loss_list.append(loss.data)
accuracy_list.append(accuracy)
iteration_list.append(iter)
# 打印信息
print("iter: {}, Loss: {}, Accu: {}%".format(iter, loss.item(), accuracy))
print()
if __name__ == '__main__':
main()
注意,上述代码并没有采用一般教程中的使用 Pytorch 代码直接下载并使用 MNIST 数据集,而是将数据集下载好后,提取出其中所有图片,保存在 raw 文件夹中,然后构造一个 DataLoader 类型的 DATA 来实现数据加载,这样可以便于我们之后将网络迁移至自己的数据集上训练。
为了便于比较,这里给出一段借助 torchvision.datasets 直接下载和加载 MNIST 数据集的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# MNIST Dataset
train_dataset = torchvision.datasets.MNIST(root='./data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = torchvision.datasets.MNIST(root='./data/',
train=False,
transform=transforms.ToTensor())
# Data Loader (Input Pipeline)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
最终也得到了用于训练和测试的 train_loader, test_loader。其中
root='./data/'表明将下载的数据集存放于代码同级路径下的 data 文件夹;train=true表明下载的数据集是用于训练的数据集;transform=transforms.ToTensor()表明对下载的数据集进行一个数据处理操作:ToTensor(object)Convert anumpy.ndarray(H x W x C) in the range [0, 255] to atorch.FloatTensorof shape (C x H x W) in the range [0.0, 1.0].download=True表明如果检测到root下没有数据集时自动下载数据所有数据,包括训练数据和测试数据,因此在train=True时设置一次即可。
PyTorch 官方给出的基于 CNN 的 MNIST 手写数字识别代码在此(https://github.com/pytorch/examples/blob/master/mnist/main.py ),以供参考。
注意到上述链接的代码中,除了 ToTensor() 之外还用到了另一个转换,Normalize() 如下:
1
2
3
4
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
总结而言,ToTensor() 能够把灰度范围从 0-255 变换到 0-1 之间,而后面的 transform.Normalize() 则把 0-1 数据执行以下操作:
1
image=(image-mean)/std
如果取 mean=0.5, std=0.5 那么 Normalize 把 0-1 数据变换到 (-1,1),号称可以加快模型收敛速度 [2]。当然此处MNIST应用时 mean=0.1307, std=0.3081 。
当 seed=0 时,即
1
2
3
4
5
6
use_cuda = torch.cuda.is_available()
device = torch.device('cuda:0' if use_cuda else 'cpu')
seed = 0
torch.manual_seed(seed)
if use_cuda:
torch.cuda.manual_seed(seed)
20 次迭代后的训练结果如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
......
EPOCH: 20
batch index: 0, images: 0/60000+[64], loss: 0.14547616243362427
batch index: 50, images: 3200/60000+[64], loss: 0.04679613187909126
batch index: 100, images: 6400/60000+[64], loss: 0.05385994166135788
batch index: 150, images: 9600/60000+[64], loss: 0.044658079743385315
batch index: 200, images: 12800/60000+[64], loss: 0.08235453814268112
batch index: 250, images: 16000/60000+[64], loss: 0.12099026888608932
batch index: 300, images: 19200/60000+[64], loss: 0.04762731492519379
batch index: 350, images: 22400/60000+[64], loss: 0.07588448375463486
batch index: 400, images: 25600/60000+[64], loss: 0.03385855257511139
batch index: 450, images: 28800/60000+[64], loss: 0.056658919900655746
batch index: 500, images: 32000/60000+[64], loss: 0.10723046958446503
batch index: 550, images: 35200/60000+[64], loss: 0.029729364439845085
batch index: 600, images: 38400/60000+[64], loss: 0.21459335088729858
batch index: 650, images: 41600/60000+[64], loss: 0.023649774491786957
batch index: 700, images: 44800/60000+[64], loss: 0.2532099485397339
batch index: 750, images: 48000/60000+[64], loss: 0.044361311942338943
batch index: 800, images: 51200/60000+[64], loss: 0.08944762498140335
batch index: 850, images: 54400/60000+[64], loss: 0.22417518496513367
batch index: 900, images: 57600/60000+[64], loss: 0.1285378485918045
iter: 18760, Loss: 0.034618619829416275, Accu: 97.50999450683594%
注意,如果不改变 seed 那么重复多次训练的结果不会变。随机数种子影响神经网络初始参数的随机初始化取值。
3. 常见错误
3.1. CUDNN_STATUS_BAD_PARAM
在 LSTM 的 forward 过程中,下述语句
1
2
def forward(self, x):
r_out, (h_n, h_c) = self.lstm(x, None)
提示 RuntimeError
1
2
3
4
发生异常: RuntimeError
cuDNN error: CUDNN_STATUS_BAD_PARAM
File "xxx.py", line xx, in forward
r_out, (h_n, h_c) = self.lstm(x, None)
参考此处(https://blog.csdn.net/daixiangzi/article/details/107671246 )
核心问题在于,LSTM 的 forward 要求输入数据的类型为 float32,而在实际代码中我们将其输入为了float64或者其它类型的数据。因此需要在输入模型训练之前进行数据转换即可解决问题
1
trainX, trainY = trainX.to(torch.float32), trainY.to(torch.float32)
4. 参考文献
[1] 谓之小一. LSTM如何解决RNN带来的梯度消失问题.
[2] 小研一枚. pytorch的transform中ToTensor接着Normalize.
[3] 姜呆. 图解LSTM——一文吃透LSTM.
[4] StatQuest. 【官方双语】LSTM(长短期记忆神经网络)最简单清晰的解释来了!.