本文介绍了深度学习中,卷积网络的基本知识,包括2d卷积层、池化层、线性层、softmax 激活函数、交叉熵损失函数等,并结合它们在 Pytorch 中的定义和实现进行说明。
1. 层
1.1. Conv2d
nn.Conv2d 的输入为 (batch_size, channel, height, width)。
nn.Conv2d 的参数包括[1]:
in_channels:int,输入图片的通道数(彩色图像=3,灰度图像=1);out_channels:int,卷积输出图片的通道数(也就是卷积核个数);kernel_size:int或tuple,卷积核尺寸(赋值单个int时长=宽),default=1;stride:int或tuple,卷积操作的滑动步长,default=1;padding:int或tuple,输入图片外围扩充大小(赋值单个int时长=宽),default=0; 当采取默认参数时,padding = (kernel_size - 1) /2 可保证输出图片与输入图片尺寸一致;dilation:卷积核扩充大小,default=1;groups:从输入通道到输出通道分组的个数,default=1;bias:bool,输出增加偏差,default=True;
假设输入数据为 $(N, C_{in}, H_{in},W_{in})$ ($N$ 张 $C_{in}$ 通道数的高 $H_{in}$ 宽 $W_{in}$ 的图片), 对于输入的每一张图片,比如第 $N_i$ 张图片,输出特征图的通道数为 $C_{out}$,具体为
\[out(N_i,C_{out,j})=bias(C_{out,j}) + \sum_{k=1}^{C_{in}}weight(C_{out,j},k)\star input(N_i,k)\]其中 $H_{out}$ 和 $H_{out}$ 为
\[\begin{aligned} H_{out} &= \frac{H_{in} + 2\times padding[0] - dilation[0]\times (kernel\_size[0]-1)-1} {stride[0]}+1 \\ W_{out} &= \frac{W_{in} + 2\times padding[1] - dilation[1]\times (kernel\_size[1]-1)-1}{stride[1]}+1 \end{aligned}\]若采 $dilation = 1$,有
\[\begin{aligned} H_{out} &= \frac{H_{in} + 2\times padding[0] - kernel\_size[0]}{stride[0]}+1 \\ W_{out} &= \frac{W_{in} + 2\times padding[1] - kernel\_size[1]}{stride[1]}+1 \end{aligned}\]若采用默认参数,有
\[\begin{aligned} H_{out} = H_{in} - kernel\_size[0] + 1 \\ W_{out} = W_{in} - kernel\_size[1] + 1 \end{aligned}\]1.1.1. dilation
注意,PyTorch 认为dilation=n 表示卷积核尺寸从 (1x1) 扩充为 nxn,其中原本的卷积核像素在左上角,其它像素填充为0。因此 dilation=1 等价于传统的无扩充的卷积[2]。
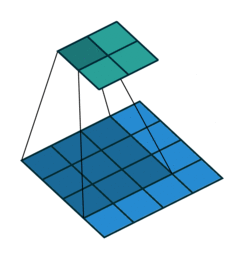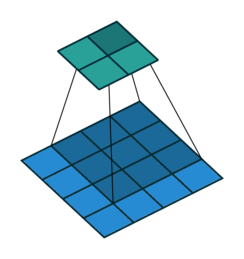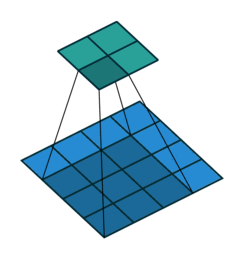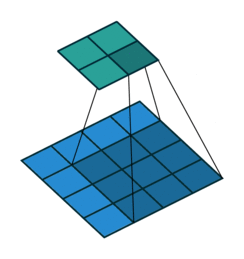
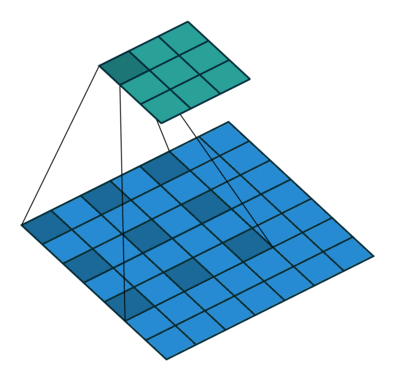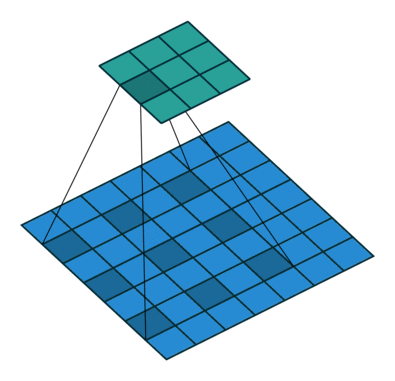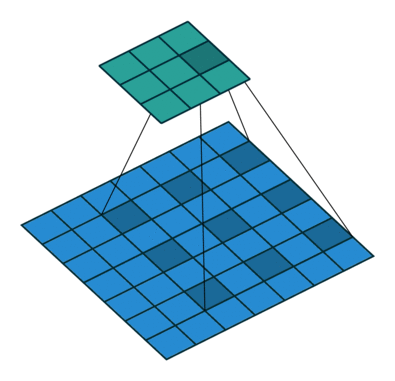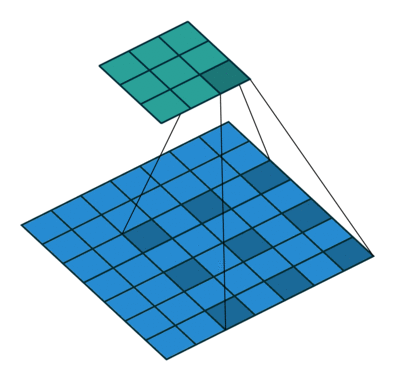
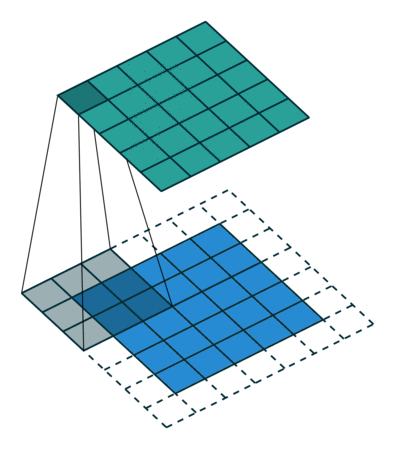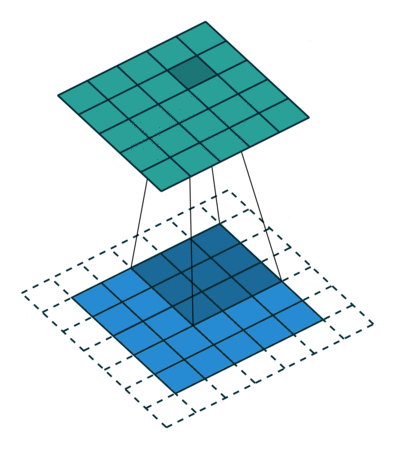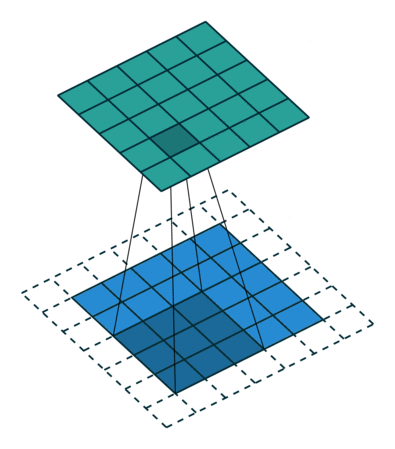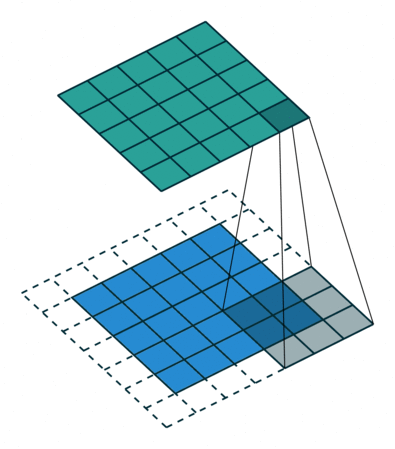
如果我们设置的 padding=0, dilation=1 的话,蓝色为输入,绿色为输出,卷积核为3*3的卷积效果如图[3]:
如果我们设置的 dilation=2 的话,卷积核点与输入之间距离为1的值相乘来得到输出
这样单次计算时覆盖的面积(即感受域)由 dilation=0 时的 $3\times 3=9$ 变为了 dilation=1 时的 $5\times 5=25$。在增加了感受域的同时却没有增加计算量,保留了更多的细节信息,对图像还原的精度有明显的提升。
1.1.2. padding
padding 是图像周围填充的像素尺寸。
在默认参数(dilation=1, padding = 0)的情况下,每经过一次卷积,图像的尺寸都会缩小。比如原始图像为 $5\times 5$,卷积核大小为 $3\times 3$,滑动步长 $stride=1$,则卷积输出的特征图为 $(5-3+1)\times (5-3+1)=3\times 3$。这样处理有两个缺点:
-
卷积后的矩阵越变越小(卷积层很多时,最终得到的将是很小的图片);
-
输入矩阵边缘像素只被计算过一次,而中间像素被卷积计算多次,意味着丢失图像角落信息。
为了保证输出尺寸与输入尺寸一致,即
\[\begin{aligned} H_{out} = H_{in} \\ W_{out} = W_{in} \end{aligned}\]需要在图像周围填充一定的像素宽度,计算匹配的 padding 值,将上面的公式变换如下
将默认的 stride=1和 dilation=1 参数代入,可得
也就是说,padding 的取值与 kernel_size 有关。如果采用长宽相等的卷积核,可简写为
对于上述例子,计算后 padding = 1。即原始图像为 $5\times 5$,图像周围填充1像素的宽度,尺寸变为$7\times 7$,经过卷积后特征图尺寸正好又变为 $5\times 5$。
1.2. MaxPool2d
nn.MaxPool2d 的参数包括:
-
kernel_size:(int or tuple) ,max pooling 的窗口大小,可以为tuple,在nlp中tuple用更多(n,1) -
stride:(int or tuple, optional) ,max pooling 的窗口移动的步长。默认值是kernel_size -
padding:(int or tuple, optional) - 输入的每一条边补充0的层数 -
dilation:(int or tuple, optional) – 一个控制窗口中元素步幅的参数 -
return_indices:如果等于True,会返回输出最大值的序号,对于上采样操作会有帮助 -
ceil_mode:如果等于True,计算输出信号大小的时候,会使用向上取整,代替默认的向下取整的操作,default=False
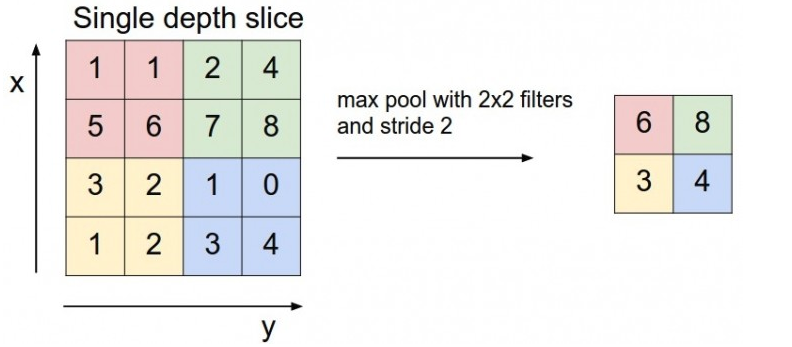
下图的 kernel_size = 2, stride = 2,将输入图片尺寸缩减为原来的一半。
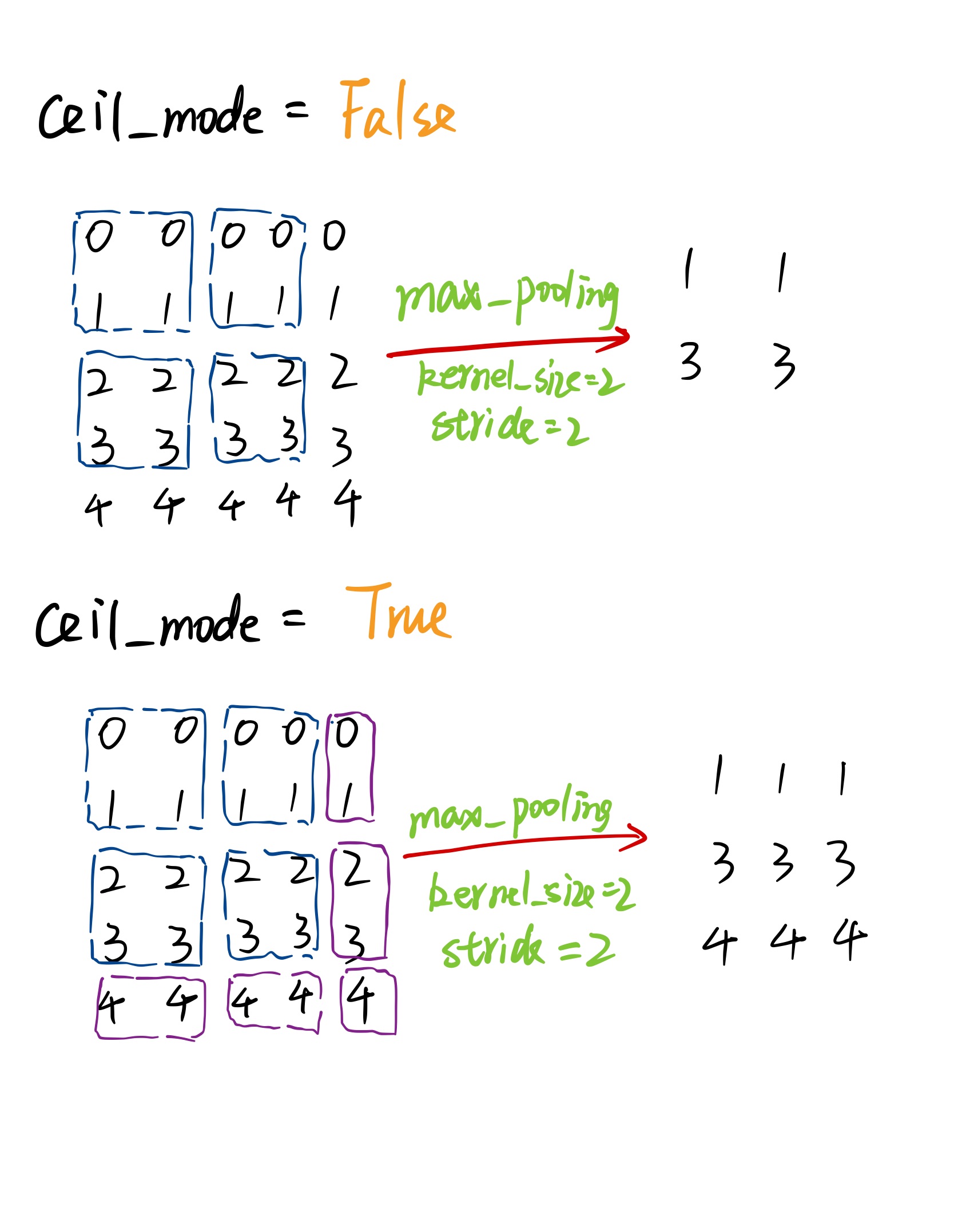
当输入无法被 kernel_size 整除时,根据 ceil_mode 来决定如何池化
1.3. Linear
nn.Linear 的参数如下:
-
in_features:输入维度;
-
out_features:输出维度;
-
bias:如果设为
False则不存在偏置,default:True。
2. 激活函数
2.1. conv2d
torch.nn 与 torch.nn.functional 差不多[4],不过一个包装好的类,一个是可以直接调用的函数。在实现源代码上,torch.nn.Conv2d 类在 forward 时调用了 torch.nn.functional.conv2d。
可能会疑惑为什么需要这两个功能如此相近的模块,其实这么设计是有其原因的。如果我们只保留nn.functional下的函数的话,在训练或者使用时,我们就要手动去维护weight, bias, stride这些中间量的值,这显然是给用户带来了不便。而如果我们只保留nn下的类的话,其实就牺牲了一部分灵活性,因为做一些简单的计算都需要创造一个类,这也与PyTorch的风格不符。
二者有一些细微的差别:
-
两者的调用方式不同。
nn.Xxx需要先实例化并传入参数,然后以函数调用的方式调用实例化的对象并传入输入数据。nn.functional.xxx同时传入输入数据和weight, bias等其他参数 。 -
nn.Xxx继承于nn.Module, 能够很好的与nn.Sequential结合使用, 而nn.functional.xxx无法与nn.Sequential结合使用。 -
nn.Xxx不需要你自己定义和管理weight;而nn.functional.xxx需要你自己定义weight,每次调用的时候都需要手动传入weight, 不利于代码复用。
两种定义方式得到CNN功能都是相同的,至于喜欢哪一种方式,是个人口味问题,但PyTorch官方推荐:
-
具有学习参数的(例如,conv2d, linear, batch_norm)采用
nn.Xxx方式 -
没有学习参数的(例如,maxpool, loss func, activation func)等根据个人选择使用
nn.functional.xxx或者nn.Xxx方式。
但关于dropout,个人强烈推荐使用nn.Xxx方式,因为一般情况下只有训练阶段才进行dropout,在eval阶段都不会进行dropout。使用nn.Xxx方式定义dropout,在调用model.eval()之后,model中所有的dropout layer都关闭,但以nn.function.dropout方式定义dropout,在调用model.eval()之后并不能关闭dropout。
2.2. softmax
我们知道 max,假如 a > b,则 max(a, b) = a ,这个结果是确定的,无论计算多少次,max 返回的值永远是 a。但有的时候我不想这样,因为这样会造成值小的那个饥饿。所以我希望分值大的那一项经常取到,分值小的那一项也偶尔可以取到。
可以采用某种方法,按照a和b本来的大小来计算取a和b的概率,就可以实现a经常取到,b也会偶尔取到。此时的选取不在遵循 max,而是 softmax 。
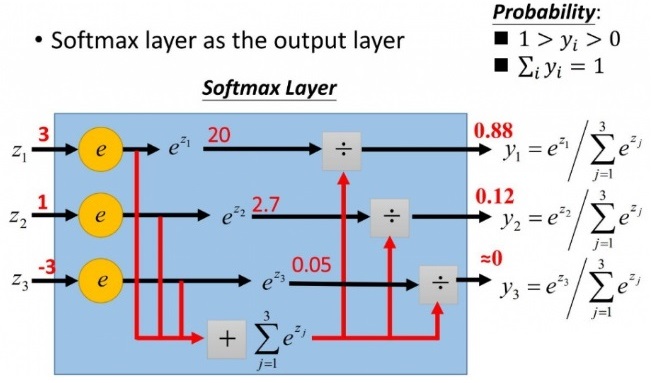
softmax 的计算方法如下,假设输入为一维向量 $Z = [z_1,z_2,…z_i,…,z_n]\in(-\infty,+\infty)$ ,则第 $i$ 个分量 $z_i$ 的 softmax 输出为
\(y_i = softmax(z_i) = \frac{e^{z_i}}{\sum_j e^{z_j}}\)
我们知道指数函数 $e^x$ 的值域为 $(0,+\infty)$ ,因此 softmax 将 $(-\infty,+\infty)$ 的值映射到 $[0, 1]$。具体来说,softmax 具备下面两个作用
- 将向量的各个维度 $z_i$ 映射为映射到 $[0, 1]$ 之间的某个值,即为该分量的取值概率;
- 向量所有维度的取值概率之和为1。
通常情况下,计算 softmax 函数值不会出现什么问题,例如,当 softmax 函数表达式里的所有 $z_i$ 都是一个 “一般大小” 的数值 $c$ 时——也就是上图中,$z_1=z_2=z_3=c$ 时,那么,计算出来的函数值 $y_1=y_2=y_3=1$。但是,当某些情况发生时,计算函数值就出问题了:
- $c$ 极其大,导致分子计算 $e^c$ 时上溢出(超出 float 表示的界限,出现 NaN)。
- $c$ 为负数,且 $\vert c\vert$ 很大,此时分母是一个极小的正数,有可能四舍五入为 $0$,导致下溢出。
解决方法为,令 $M = max(z_i), i =1,2,3,….,n$,计算 $softmax(z_i - M)$ 的值,就可以解决上溢出、下溢出的问题了,并且,计算结果理论上仍然和 $softmax(z_i)$ 保持一致。具体而言:
-
$z_i - M$ 的取值范围为 $(-\infty,0]$ ,因此在做指数运算时输入的最大值为 0,从而避免上溢出。
-
$softmax(z_i - M)$ 的值域为 $[0,1]$ ,因为分母对所有指数求和时,至少有一个指数(对应输入最大值0的指数项)为1,保证了分母不为0,从而避免下溢出。
1
2
# dim=0 makes sum of column values to be 1, dim=1 makes row ...
softmax(input, dim=-1)
2.3. log_softmax
在 softmax 的基础上多做一个 log 运算,log_softmax号称能够加快运算速度,提高数据稳定性。在数学上等价于 log(softmax(x)) ,但做这两个单独操作速度较慢,数值上也不稳定。
log_softmax 的值域为 $(-\infty, 0]$。
3. 损失函数
3.1. CrossEntropyLoss
交叉熵损失函数。在说交叉熵之前,先说一下信息量与熵。
信息量:衡量一个事件的不确定性;一个事件发生的概率越大,不确定性越小,则它所携带的信息量就越小。假设 $X$ 是一个离散型随机变量,其取值集合为 $X$,概率分布函数为 $p(x)=P(X=x),x\in X$ ,我们定义事件 $X=x_0$ 的信息量为:$I(x_0)=-log(p(x_0))$。当 $p(x_0) = 1$ 时,熵等于0,也就是说该事件的发生不会导致任何信息量的增加。
熵:用来衡量一个系统的混乱程度,代表一个系统中信息量的总和;信息量总和越大,系统不确定性越大。
对所有可能事件所带来的信息量求期望,其结果就能衡量事务的不确定度。
交叉熵:它主要刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布 $p$ 为期望输出,概率分布 $q$ 为实际输出, $H(p,q)$ 为交叉熵。其计算方法有两种 \(H(p,q)=-\sum_i (p_i log q_i + (1-p_i)log(1-q_i))\)
或者
\[H(p,q) = -\sum_i (p_ilog q_i)\]假设某个样本对应的标签 $y = [y_1,y_2,…,y_K]\in R^K$ 为一个向量,PyTorch 中的交叉熵损失函数形式如下
\[L = -\sum_{i=1}^K (y_ilog s_i)\]其中,$y_i$ 为真实分类值,$s_i$ 为 softmax 输出值,$i$ 代表神经元节点的标号。
假设网络结构为 xx -> Linear -> softmax,即一个全连接层的输出作为 softmax 的输入,有
采用交叉熵损失函数,则损失函数对 softmax 的倒数为
由于全连接层
\[\begin{aligned} \frac{\partial z_i}{\partial w_i} &= x_i \\ \frac{\partial z_i}{\partial b_i} &= 1 \end{aligned}\]则核心问题变为求解 $\frac{\partial L}{\partial z_i}$ 。
\[\begin{aligned} \frac{\partial z_i}{\partial w_i} &= x_i \\ \frac{\partial z_i}{\partial b_i} &= 1 \end{aligned}\]由于 softmax 的计算公式中,任意一个 s_i 均包含 z 的所有分类,因此有
根据损失函数的定义,有
\[\frac{\partial L}{\partial s_k}=-\frac{y_k}{s_k}\]下面求解 $\frac{\partial s_k}{\partial z_i}$ ,需要分情况讨论
当 $k \neq i$ 时,有
\[\begin{aligned} \frac{\partial s_k}{\partial z_i} &= \frac{\partial(\frac{e^{z_k}}{\sum_j e^{z_j}})}{\partial z_i}\\ &= e^{z_k}\frac{\partial(\frac{1}{\sum_j e^{z_j}})}{\partial z_i}\\ &= e^{z_k}(-\frac{1}{(\sum_j e^{z_j})^2})\frac{\partial \sum_j e^{z_j}}{\partial z_i}\\ &= e^{z_k}(-\frac{1}{(\sum_j e^{z_j})^2})e^{z_i}\\ &= -(\frac{e^{z_k}}{\sum_j e^{z_j}})(\frac{e^{z_i}}{\sum_j e^{z_j}}) = -s_k\cdot s_i \end{aligned}\]当 $k=i$ 时,有(分式求导法则:上导下不导减下导上不导除以下的平方)
\[\begin{aligned} \frac{\partial s_k}{\partial z_i} &=\frac{\partial s_i}{\partial z_i}\\ &=\frac{\partial(\frac{e^{z_i}}{\sum_j e^{z_j}})}{\partial z_i}\\ &=\frac{e^{z_i}\sum_j e^{z_i}-(e^{z_i})^2}{(\sum_j e^{z_i})^2}\\ &=\frac{e^{z_i}}{\sum_j e^{z_i}}\frac{\sum_j e^{z_i}-e^{z_i}}{\sum_j e^{z_i}}\\ &=\frac{e^{z_i}}{\sum_j e^{z_i}}(1-\frac{e^{z_i}}{\sum_j e^{z_i}}) = s_i(1-s_i) \end{aligned}\]最终得到
\[\begin{aligned} \frac{\partial L}{\partial z_i} &= -\frac{y_i}{s_i}s_i(1-s_i)+\sum_{k \neq i}(-\frac{y_k}{s_k}\cdot-s_ks_i)\\ &= -y_i + \sum_{k=1}^K y_k \end{aligned}\]对于多分类问题,样本真实标签 $y = [y_1,y_2,…,y_K]$ 是one-hot,即只有一个元素为1,其余元素为0。那么有 $\sum_{k=1}^K y_k = 1$,因此在多分类问题中
\[\frac{\partial L}{\partial z_i} = s_i - y_i\]那么有
\[\begin{aligned} \frac{\partial L}{\partial \omega_i} &= (s_i - y_i)\cdot x\\ \frac{\partial L}{\partial b_i} &= s_i - y_i \end{aligned}\]3.2. NLLLoss
负对数似然损失函数(Negative Log Likelihood, NLL) 的 输入是一个对数概率向量和一个目标标签。它不会为我们计算对数概率,适合网络的最后一层是 log_softmax。
NLLLoss 的数学形式为
\(L(X,label) = -X_{label}\)
其中,X 是 log_softmax 的输出,label 是对应的标签位置,即 NLLLoss 的输出是取 X 中对应于 label 中为1的那个 x 。
在分类问题中,CrossEntropy 等价于 log_softmax + nll_loss,也就是说如果使用 CrossEntropy,则前面不要加 softmax 层,因为 CrossEntropy 中内含 softmax。而如果使用 nll_loss,前面就必须要使用 log_softmax 层。
理论上,对于单标签多分类问题,直接经过 softmax 求出概率分布,然后把这个概率分布用 CrossEntropy 做一个似然估计误差。但是 softmax 求出来的概率分布,每一个概率都是 $(0, 1)$ 的,这就会导致有些概率过小,导致下溢。 考虑到这个概率分布总归是要经过 CrossEntropy的,而 CrossEntropy的计算是把概率分布外面套一个 -log 来似然,那么直接在计算概率分布的时候加上 log,把概率从 $(0, 1)$ 变为 $(-\infty, 0)$,这样就防止中间会有下溢出。 所以 log_softmax 说白了就是将本来应该由 CrossEntropy做的 log 的工作提到预测概率分布来,跳过了中间的存储步骤,防止中间数值会有下溢出,使得数据更加稳定。 正是由于把log这一步从计算误差提到前面,所以用 log_softmax 之后,下游的损失函数就应该变成 NLLLoss(它没有套 log 这一步,直接将输入取反,然后计算和标签的乘积求和平均)。
4. 参考文献
[1] PyTorch. Conv2d.
[2] Stack Overflow. Default dilation value in PyTorch.
[3] Vincent Dumoulin, Francesco Visin. A guide to convolution arithmetic for deep learning (Github).
[4] 知乎. PyTorch 中,nn 与 nn.functional 有什么区别?.
[5] PyTorch. MaxPool2d.
[6] PyTorch. nn.Linear.