强化学习（动态规划）
本文介绍了强化学习的动态规划法（Dynamic Programming，DP），采用动态规划的思想，分别介绍策略迭代和价值迭代方法。
1. 强化学习问题的求解
强化学习的最终目标是为了求解最优策略，而最优策略一定对应着最优的价值函数（只要知道了最优价值函数就能很轻松的得到最优策略），因此可将强化学习的目标分解为以下两个基本问题：
- 预测问题，也即预测给定策略的状态价值函数。给定强化学习的6个要素：状态集$S$, 动作集$A$, 模型状态转移概率矩阵$P$, 即时奖励$R$，衰减因子$\gamma$, 给定策略$\pi$， 求解该策略的状态价值函数$v_\pi(s)$ 或动作价值函数 $q_\pi(s,a)$；
- 控制问题，也即求解最优的价值函数和策略。给定强化学习的5个要素：状态集$S$, 动作集$A$, 模型状态转移概率矩阵$P$, 即时奖励$R$，衰减因子$\gamma$, 求解最优的状态价值函数$v_{\star}$ 和最优策略 $\pi_{\star}$。
2. 动态规划
动态规划（Dynamic Programming，DP）是一种将复杂问题简单化的思想，而不是指某种具体的算法。DP算法通过把复杂问题分解为子问题，通过求解子问题进而得到整个问题的解。在解决子问题的时候，其结果通常需要存储起来被用来解决后续复杂问题。
一个复杂问题可以使用DP思想来求解，只要满足两个性质就可以：(1)一个复杂问题的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解；(2)子问题在复杂问题内重复出现，使得子问题的解可以被存储起来重复利用。
巧了，强化学习要解决的问题刚好满足这两个条件。还记得贝尔曼方程吗？
\[\begin{aligned} v(s)& \leftarrow\mathbb{E}_\pi[R_{t+1}+\gamma v(s^\prime)]\\ \Rightarrow v(s) & = \sum_{a\in A}\pi(a\vert s)[R_s^a+\gamma \sum_{s^\prime \in S}P_{ss^\prime}^a v(s^\prime)]\\ \end{aligned}\]不难发现，当模型已知时（即 $A,P_{ss^\prime}^a, R_s^a$ 已知），我们可以定义出子问题求解每个状态的状态价值函数，同时这个式子又是一个递推的式子, 意味着利用它，我们可以使用上一个迭代周期内的状态价值来计算更新当前迭代周期某状态 $s$ 的状态价值（详见策略迭代）。可见，使用动态规划来求解强化学习问题是比较自然的。
此处有一个概念：值函数的计算用到了bootstapping的方法。所谓bootstrpping本意是指自举，此处是指当前值函数的计算用到了后继状态的值函数，也即用后继状态的值函数计算当前值函数。
动态规划要求马尔可夫决策过程五元组完全已知，即 $<S,A,P,R,\gamma>$ 是完全确定的。在求解强化学习问题时，动态规划方法就是一种基于模型的方法（model-based）。
2.1. 策略迭代
知道了动态规划与强化学习的联系，我们就能用DP的思想去求解强化学习问题。策略迭代包括策略评估（Policy Evaluation）和策略改进（Policy Improvement），其基本过程是从一个初始化的策略出发，先进行策略评估，然后策略改进，评估改进的策略，再进一步改进策略，经过不断迭代更新，直到策略收敛。
下面具体介绍策略评估和策略改进。
2.1.1. 策略评估
- 解析求解
记
\[\begin{aligned} v_\pi &\doteq [v_\pi(s_1)\; v_\pi(s_2)\; \cdots]^T_{n\times 1}\\ r_\pi &\doteq [r_\pi(s_1)\; r_\pi(s_2)\; \cdots]^T_{n\times 1}\\ P_\pi &\doteq [P_\pi(s,s^\prime)]_{n\times n} \end{aligned}\]根据贝尔曼期望方程，可以看出其是一个关于 $v_\pi(s)$ 的线性方程
\[\begin{aligned} v_\pi(s) =& \sum_a \pi(a\vert s) \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a) [ r+\gamma v_\pi(s^\prime) ]\\ =&\sum_a \pi(a\vert s) \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a)r\\ &+\gamma \sum_a \pi(a\vert s) \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a)v_\pi(s^\prime)\\ \end{aligned}\]其中第一项（积掉 $s^\prime$）
\[\begin{aligned} &=\sum_a \pi(a\vert s) \sum_r p(r \vert s,a) r\\ &= \sum_a \pi(a\vert s) \mathbb{E}_\pi[R_{t+1}\vert s,a]\\ &\doteq \sum_a \pi(a\vert s) r(s,a)\quad （定义r(s,a)）\\ &\doteq r_\pi(s)\quad \quad \quad \quad \quad \quad （定义r_\pi(s)） \end{aligned}\]其中第二项（积掉 $r$）
\[\begin{aligned} &=\gamma \sum_a \pi(a\vert s) \sum_{s^\prime} p(s^\prime \vert s,a)v_\pi(s^\prime)\\ &=\gamma \sum_{s^\prime} \sum_a \pi(a\vert s) p(s^\prime \vert s,a)v_\pi(s^\prime)\\ &\doteq\gamma \sum_{s^\prime} P_\pi(s,s^\prime)v_\pi(s^\prime)\quad （积掉a，定义P_\pi(s,s^\prime)）\\ \end{aligned}\]于是有
\[\begin{aligned} v_\pi(s) =& r_\pi(s) + \gamma \sum_{s^\prime} P_\pi(s,s^\prime) v_\pi(s^\prime) \end{aligned}\]令 $s_i = s, s_j = s^\prime$ 有
\[\begin{aligned} v_\pi(s_i) =& r_\pi(s_i) + \gamma \sum_{j=1}^n P_\pi(s_i,s_j) v_\pi(s_j)\\ \Rightarrow V_\pi &= R_\pi + \gamma P_\pi V_\pi \quad （上式即为该式第i行）\\ \Rightarrow V_\pi &= (I-\gamma P_\pi)^{-1}R_\pi \end{aligned}\]上述计算复杂度为 $O(n^3)$（$n$ 阶矩阵求逆时间复杂度为$O(n^3)$，相乘时间复杂度为$O(n^3)$，二者顺序执行时间复杂度为$2O(n^3)$，但考虑计算复杂度时不用考虑系数）。当状态维度较高时，上述计算过于复杂，因此用后面的迭代求解方法。
- 迭代求解
策略评估迭代求解的基本思路是从任意初始的策略和初始的状态价值函数开始，结合贝尔曼方程、状态转移概率和奖励，同步迭代更新状态价值函数，直至其收敛，得到该策略下最终的状态价值函数。策略评估旨在求解预测问题。
假设给定一个策略 $\pi$，和初始时刻所有状态的状态价值 $v_0(s)$。
第 $k$ 轮迭代，已经计算出所有状态价值，则第 $k+1$ 轮迭代如何计算？
可以结合贝尔曼方程构造第 $k+1$ 轮迭代的状态价值函数如下
\[\begin{aligned} v_{\color{red}{k+1}}(s) \doteq & \sum_{a\in A}\pi(a\vert s)[R_s^a+\gamma \sum_{s^\prime \in S}P_{ss^\prime}^a v_{\color{red}k}(s^\prime)]\\ & = \sum_{a\in A}\pi(a\vert s)\sum_{s\prime, r}p(s^\prime,r \vert s, a)[r+\gamma v_{\color{red}k}(s^\prime)] \end{aligned}\]问题转化为上式是否收敛？是否收敛到 $v_\pi$？（此处略）
为了使用顺序执行的计算机程序实现策略评估，我们需要构造两个数组：一个用于存储旧的价值函数 $v_k(s)$，一个用于存储新的价值函数 $v_{k+1}(s)$。这样，在旧的价值函数不变的情况下，新的价值函数可以一个个被计算出来。同样，也可以简单使用一个数组来进行就地更新（in-place），即每次直接使用新的价值函数替换旧的价值函数。这种就地更新的方式依然可以保证收敛到$v_\pi$，并且收敛速度更快。就地更新时的价值函数迭代式子如下：
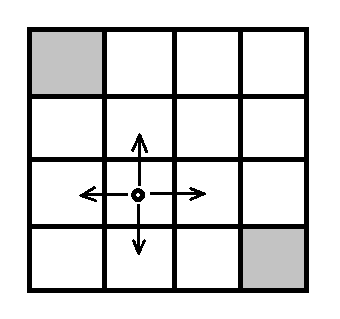
\[{\color{red}v(s)} \leftarrow \sum_a \pi(a\vert s) \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma {\color{red}v(s^\prime)}]\]下面给出一个经典的 Grid World 例子。假设有一个4x4的16宫格。只有左上和右下的格子是终止格子。该位置的价值固定为0，个体如果到达了该两个格子，则停止移动，此后每轮奖励都是0。注意个体每次只能移动一个格子，且只能上下左右4种移动选择，不能斜着走, 如果在边界格往外走，则会直接移动回到之前的边界格。
下面对问题进行定义：
- $R_s^a=-1$，即个体在16宫格其他格的每次移动，得到的即时奖励都为-1。
- $\gamma=1$，即奖励的累计不衰减。
- $P_{ss^\prime}^a=1$，即每次移动到的下一格都是固定的（如往上走一定到上面的格子），不考虑转移不确定的情况；
- $\pi(a\vert s) = 0.25, \forall a\in A$，即给定随机策略，每个格子里有25%的概率向周围的4个格子移动。
至此，马尔可夫决策过程的所有参数均已知，下面进行状态价值函数预测。
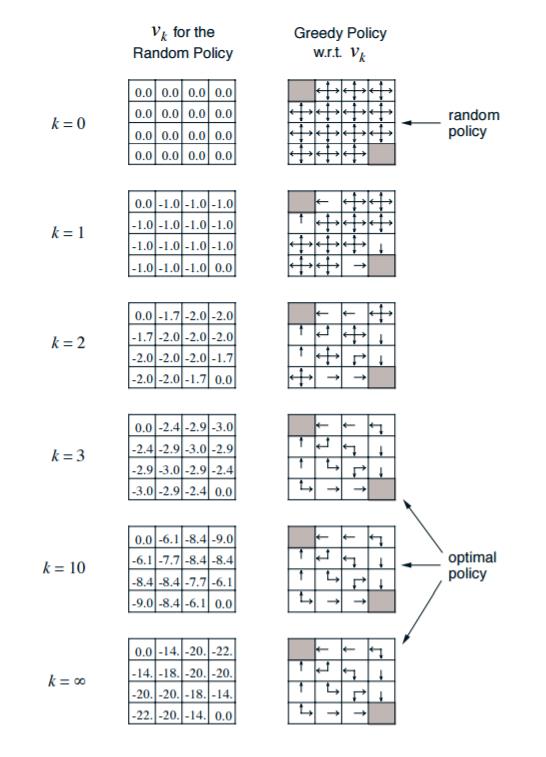
$k=1$ 时，带入贝尔曼方程，计算第二行第一个格子的价值（其他的格子类似）
\[v_1^{21}=0.25[(-1+0(up))+(-1+0(down))+(-1+0(left))+(-1+0(right))]=-1\]$k=2$ 时，继续计算第二行第一个格子的价值（其他的格子类似）
\[v_2^{21}=0.25[(-1+0(up))+(-1-1(down))+(-1-1(left))+(-1-1(right))]=-1.75\]如此迭代直至每个格子的状态价值改变很小为止。这时我们就得到了所有格子的基于随机策略的状态价值。
可以看到，动态规划的策略评估计算过程并不复杂，但是如果我们的问题是一个非常复杂的模型的话，这个计算量还是非常大的。
2.1.2. 策略改进
在给定策略 $\pi$ 的条件下，通过上面的策略评估可以迭代计算得到价值函数，但仍然没有得到最优策略。因为如果从状态 $s$ 开始执行现有策略，最终结果就是 $v_\pi(s)$，但我们不知道是否有更好的策略。那么如何进行策略改进呢？我们可以利用 “策略改进定理” 来实现。
- 策略改进定理
策略改进定理 给定 $\pi,\pi^\prime$， 如果 $\forall s\in S, q_\pi(s,\pi^\prime(s))\geq v_\pi(s)$， 那么有 $\forall s\in S, v_{\pi^\prime}(s)\geq v_\pi(s)$， 即 $\pi^\prime \geq \pi$。
证明如下：
\[\begin{aligned} v_\pi(s) &\leq q_\pi(s,\pi^\prime(s))\\ &=\mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})\vert S_t=s,A_t = \pi^\prime(s)]\\ &=\mathbb{E}_{\pi^\prime}[R_{t+1}+\gamma v_\pi(S_{t+1})\vert S_t=s]\quad (走1步：R_{t+1}由\pi^\prime 控制，后面由\pi控制)\\ &\leq \mathbb{E}_{\pi^\prime}[R_{t+1}+\gamma q_\pi(S_{t+1},\pi^\prime(S_{t+1}))\vert S_t=s]\\ &=\mathbb{E}_{\pi^\prime}[R_{t+1}+\gamma \mathbb{E}_{\pi^{\prime}}[R_{t+2}+\gamma v_\pi(S_{t+2})\vert S_{t+1}] \vert S_t=s]\quad （前式带入）\\ &=\mathbb{E}_{\pi^\prime}[R_{t+1}+\gamma \mathbb{E}_{\pi^{\prime}}[R_{t+2}\vert S_{t+1}]+\gamma^2 \mathbb{E}_{\pi^{\prime}} [v_\pi(S_{t+2}) \vert S_{t+1} ] \vert S_t=s]\\ &=\mathbb{E}_{\pi^\prime}[R_{t+1}+R_{t+2}+\gamma^2 v_\pi(S_{t+2})\vert S_t=s] \quad （走2步）\\ &=\cdots\\ &=\mathbb{E}_\pi^\prime[R_{t+1}+\gamma R_{t+2}+\cdots \vert S_t=s] \\ &= v_{\pi^\prime}(s) \end{aligned}\]参考推导见：策略改进定理及证明中隐式期望的处理
基于以上证明，我们知道策略改进是切实可行的，那么究竟怎么做才能更新策略呢？
- 贪心方法
我们知道：
\[v_{\pi}(s) = \mathbb{E}_{a}[q_{\pi}(s,a)]\]而根据期望的定义，最大的 $q$ 函数肯定是大于等于其期望的，即
\[q_\pi(s,a)_{max} \geq v_\pi(s)\]那么我们每次都选择使得 $q_\pi(s,a)$ 最大的那个动作，构成策略，就可以保证满足策略改进定理，构成的策略就是更好的策略了！这就是贪心方法。
具体而言，在当前策略对应的状态价值函数下，智能体在每个状态都计算一下所有动作各自的状态-动作价值函数，选出值最大的执行就可以。贪心方法如下：
\[\forall s\in S,\; \pi^\prime(s) = \left\{ \begin{aligned} 1, \quad & a=\mathop{argmax}\limits_a\; q_\pi(s,a) \\ 0, \quad & otherwise \end{aligned} \right.\]证明：
\[\forall s\in S,\; v_\pi(s) = \mathbb{E}_a[q_\pi(s,a)] \leq max_a q_\pi(s,a) = max_a q_\pi(s,\pi^\prime(s))\]满足策略改进定理条件，因此有
\[\forall s\in S,\;v_{\pi^\prime}(s) \geq v_\pi(s)\]得证。
因此，策略改进定理提供了一种更新策略的方式：对每个状态 $s$ ，寻找贪婪动作 $\mathop{argmax}\limits_a q_\pi(s,a)$ ，以贪婪动作作为新的策略 $\pi^\prime$ ，根据策略改进定理必然有 $\pi^\prime \geq \pi$ 。
依然是 Grid World 例子，前面我们给定一个随机策略 $\pi(a\vert s) = 0.25, \forall a\in A$，并得到了其对应的状态价值函数。
根据前面的策略改进定理，可以采用贪婪法来改进我们的这个策略。具体而言，个体在某个状态下选择的行为是其能够到达后续所有可能的状态中状态价值最大的那个状态，如上图右侧所示，最终求解控制问题。
当我们计算出最终的状态价值后，我们发现：
- 第二行第一个格子周围的价值分别是0,-18,-20，此时我们用贪婪法，则我们调整行动策略为向状态价值为0的方向（上方）移动，而不是随机移动。而此时
- 第二行第二个格子周围的价值分别是-14,-14,-20, -20。那么我们整行动策略为向状态价值为-14的方向（左或者上）移动。
- ……以此类推。
注意到：上述过程的策略是基于最大的 $v_\pi(s)$，但实际上应该根据 $q_\pi(s,a)$ 来调整策略 $q_\pi(s,a) = \mathbb{E}[R_{t+1}+\gamma v_\pi(s^\prime) ]$ 但由于本例中，所有可行的的状态转化概率P=1，瞬时奖励都是-1，衰减因子定义为1，所以其实 $q$ 函数的值就是下一个状态的状态价值 $v$，这也就是为什么直接往状态价值最大的那个状态移动就可以的原因。
总结，策略迭代就是在循环进行两部分工作，第一步是使用当前策略 $\pi$ 评估计算当前策略的最终状态价值 $v$，第二步是根据状态价值 $v$ 根据一定的方法（比如贪婪法）更新策略 $\pi$，接着回到第一步，一直迭代下去，最终得到收敛的策略 $\pi_{\star}$ 和状态价值 $v_∗$。
2.1.3. 策略迭代
最终的策略迭代的算法表述如下：
- 初始化
- 对于所有 $s\in S$，任意初始化$V(s)$ 和 $\pi(s)$
- 给定 $p(s^\prime,r\vert s,a)$ 和 $r$ 和 $\gamma$
- 给定一个很小的正整数 $\theta$
- 策略评估
- 循环($k$)：
- $\Delta = 0$
- 对于每个 $s\in S$：
- $v \leftarrow v_k(s)$
- $v_{k+1}(s) =\sum_a \pi(a\vert s) \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma v_{k}(s^\prime)]$
- $\Delta = max(\Delta, v-v_{k+1}(s))$
- 直至 $\Delta < \theta$ （$v(s)$收敛）
- 循环($k$)：
- 策略改进
- $policy\;stable \leftarrow true$
- 对于每个 $s\in S$：
- $a_{old} = \pi(s)$
- $q_\pi(s,a) = \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma v(s^\prime)]$
- $\pi(s)\leftarrow \mathop{argmax}\limits_a\; q_\pi(s,a) $ （贪婪法）
- 如果 $a_{old} \neq \pi(s)$ 那么 $policy\;stable \leftarrow false$
- 如果 $policy\;stable \leftarrow true$，停止迭代，得到 $v_\star\approx v, \pi_\star\approx \pi$；否则返回步骤 2
线性化示意图如下（含有 $v$ 迭代和 $\pi$ 迭代两层迭代）：
\[v_1 \rightarrow \cdots \rightarrow v_{\star} \rightarrow \pi_1 \rightarrow v_2 \rightarrow \cdots \rightarrow \pi_2 \rightarrow\]2.2. 价值迭代
在策略迭代中，状态价值函数在策略评估过程中时通过迭代的形式计算的，这非常耗时。而且我们在迭代计算状态价值函数的时候策略并不是最优的，用一个非最优的策略来计算完全准确的状态价值函数并没有太大意义。由于策略迭代通常在迭代几次后就可以收敛（上文中的 Grid World 例子，第三次迭代后，策略就已经达到最优），因此我们可以提前截断策略评估过程。
一种重要的特殊的情况是，在一次遍历后即刻停止策略评估（对每一个状态进行一次更新），该算法被称为价值迭代。
价值迭代算法是策略评估过程只进行一次迭代的策略迭代算法，其过程为 ：对每一个当前状态 $s$ ，对每个可能的动作 $a$ 都计算一下采取这个动作后到达的下一个状态的期望价值。选择最大的期望价值函数作为当前状态的价值函数 $v(s)$ ，循环执行这个步骤，直到价值函数收敛。
价值迭代的算法表述如下：
- 初始化
- 对于所有 $s\in S$，任意初始化$V(s)$ 和 $\pi(s)$
- 给定 $p(s^\prime,r\vert s,a)$ 和 $r$ 和 $\gamma$
- 给定一个很小的正整数 $\theta$
- 策略评估
- 循环($k$)：
- $\Delta = 0$
- 对于每个 $s\in S$：
- $v \leftarrow v_k(s)$
- $v_{k+1}(s) \leftarrow {\color{red}max_a} \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma v_{k}(s^\prime)]\qquad$ 贝尔曼最优方程
- $\Delta = max(\Delta, v-v_{k+1}(s))$
- 直至 $\Delta < \theta$ （$v(s)$收敛）
- 循环($k$)：
- 策略改进
- $q_\pi(s,a) = \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma v(s^\prime)]$
- $\pi(s)\leftarrow \mathop{argmax}\limits_a\; q_\pi(s,a) $
可以看出：
- 更新目标：根据
max操作符我们可以发现，价值迭代的更新目标不再是 $v_\pi$ ，公式中没有任何显示的策略 $\pi$ 的影子，反之，其更新目标正是最优价值函数（也即最优策略），一旦价值迭代收敛，基于其产生的贪婪策略就是最优策略； - 更新方式： 从 $\sum_{s^\prime,r}p(s^\prime,r\vert s,a)$ 项我们可以看出，依然是期望更新的方式，这一点和策略评估是一致的。不同之处在于策略评估中的 $\pi(s)$ 被更换为了具有最大价值的 $a$ ，即策略迭代中策略评估估计状态价值采用了关于策略分布的期望，而价值迭代中的策略评估采用了最大值；
线性化示意图如下（只含有 $v$ 迭代）：
\[v_1 \rightarrow \cdots \rightarrow v_2 \rightarrow \cdots \rightarrow v_{\star} \rightarrow \pi_{\star}\]可以看出，价值迭代是极端情况下的策略迭代。
价值迭代中同样需要存储两份状态价值函数 $v_{k+1}(s),\; v_k(s)$，实际上也可以只保存一份，即采用就地更新方法，此时迭代式变为
\[{\color{red}v(s)} \leftarrow max_a \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma {\color{red}v(s^\prime)}]\]2.3. 异步动态规划
每次进行价值估计和更新时都要对全部的状态进行一次遍历，这未免太过繁琐，尤其是当状态空间足够大时，消耗在遍历上的资源就不尽人意了。那能不能一次更新只针对部分状态进行呢？只更新部分状态还能保证价值更新的收敛吗？
可以的。
在异步动态规划算法中，每一次迭代并不对所有状态的价值进行更新，而是依据一定的原则有选择性地更新部分状态的价值，这种算法能显著节约计算资源，并且只要所有状态能够得到持续的访问更新，那么也能确保算法收敛至最优解。 下面分别介绍比较常用的异步动态规划思想：
- 原位动态规划 (in-place dynamic programming)：直接利用当前状态的后续状态的价值来更新当前状态的价值。
- 优先级动态规划 (prioritised sweeping)：对每一个状态进行优先级分级，优先级越高的状态其状态价值优先得到更新。
- 实时动态规划 (real-time dynamic programming)：直接使用个体与环境交互产生的实际经历来更新状态价值，对于那些个体实际经历过的状态进行价值更新。
3. 参考文献
[1] 刘建平Pinard. 强化学习（三）用动态规划（DP）求解.
[2] Zeal. 知乎：强化学习二：策略迭代法
[3] shuhuai008. bilibili【强化学习】动态规划【白板推导系列】
[4] 韵尘. 知乎：4.2 —— 策略改进（Policy Improvement）（含收敛性证明）