本文介绍了 RNN (循环神经网络)的基本概念,以及正/反向传播的推导过程。最后分析了 RNN 的梯度消失和梯度爆炸问题。
1. RNN
1.1. 概念
在前馈神经网络中,信息传递是单向的[1]。前馈神经网络可以看作一个复杂的函数,每次输入都是独立的,即网络的输出只依赖于当前的输入.但是在很多现实任务中,网络的输出不仅和当前时刻的输入相关,也和其过去一段时间的输出相关。此外,前馈网络难以处理时序数据,比如视频、语音、文本等.时序数据的长度一般是不固定的,而前馈神经网络要求输入和输出的维数都是固定的,不能任意改变.因此,当处理这一类和时序数据相关的问题时,就需要一种能力更强的模型.
循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络.在循环神经网络中,神经元不但可以接受其他神经元的信息,也可以接受自身的信息,形成具有环路的网络结构.和前馈神经网络相比,循环神经网络更加符合生物神经网络的结构.循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。
RNN 用于分类的简单例子参考:
根据人名判断国家:字符级 RNN 对单词分类。输入人名单词,将每个字符进行编码后读取(one-hot),在每一步输出预测和“隐藏状态”,将其先前的隐藏状态输入至下一时刻。将最终时刻输出作为预测结果,即表示该词属于哪个类(哪个国家的人名)。
根据句子判断语言:单词级 RNN 对句子分类。输入一个句子,将每个单词进行编码后读取(word2vec),在每一步输出预测和“隐藏状态”,将其先前的隐藏状态输入至下一时刻。将最终时刻输出作为预测结果,即表示该词属于哪个类(哪个国家的语言)。
上述例子中,输入是对 字符 / 单词 序列的编码,编码方式可以是 one-hot 形式也可以采用 word2vec 方法。期望输出一般是一个 one-hot 向量,比如 10 种国家 / 语言,预测输出一般是一个多分类概率结果。
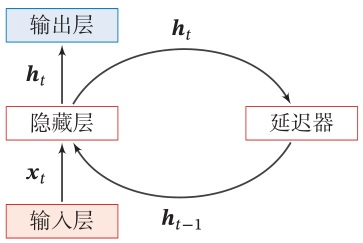
1.2. 模型
循环神经网络(Recurrent Neural Network,RNN)通过使用带自反馈的神经元,能够处理任意长度的时序数据。
给定一个输入序列 $\boldsymbol x_{1:T} = (\boldsymbol x_1,…,\boldsymbol x_t,…,\boldsymbol x_T)$,通过下面的公式更新隐层活性值 $\boldsymbol h_t$:
\[\boldsymbol h_t = f(\boldsymbol h_{t-1},\boldsymbol x_t)\]其中,$\boldsymbol h_0 = 0$,$f(\cdot)$ 是非线性函数,可以是一个前馈网络。
网络结构如下图所示
从数学上讲,上述公式可以堪称一个动力系统,因此隐层活性值在很多文献中也称为隐状态(hidden state)。
由于循环神经网络具有短期记忆能力,因此其计算能力十分强大,可以近似任意非线性动力系统(程序),相比较而言,前馈神经网络可以模拟任何连续函数。
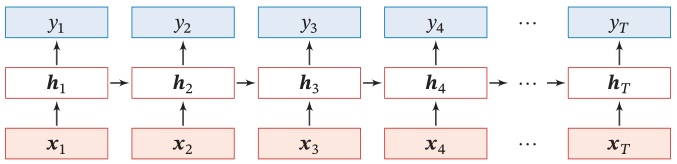
1.3. 前向传播
如果我们把每个时刻的状态都看作前馈神经网络的一层,循环神经网络可以看作在时间维度上权值共享的神经网络。一个简单的循环神经网络按时间展开后如下图所示
令 $\boldsymbol x_t \in \mathbb R^M$ 为 $t$ 时刻的网络输入向量,则在该时刻的网络隐状态 $\boldsymbol h_t \in \mathbb R^D$ 和网络输出 $\boldsymbol y_t \in \mathbb R^N$ 的更新公式为
\[\begin{aligned} \boldsymbol h_t &= f(\boldsymbol U \boldsymbol h_{t-1} + \boldsymbol W \boldsymbol x_t + \boldsymbol b)\\ \boldsymbol y_t &= g(\boldsymbol V \boldsymbol h_t + \boldsymbol c) \end{aligned}\]其中 $\boldsymbol U \in \mathbb R^{D\times D}$ 是状态-状态权重矩阵,$\boldsymbol W \in \mathbb R^{D\times M}$ 是状态-输入权重矩阵,$\boldsymbol b \in \mathbb R^D, \boldsymbol c \in \mathbb R^N$ 是偏置向量,$\boldsymbol V \in \mathbb R^{N\times D}$ 是状态-输出权重矩阵,$f(\cdot)$ 是激活函数,如 $sigmoid$ 或 $tanh$ 函数,$g(\cdot)$ 也是激活函数,如 $softmax$ 或 $purlin$ 函数。
注意到,第二个方程的具体形式与模型的具体使用方式有关,比如其中的常数项 $\boldsymbol c$ 的有无,激活函数 $g(\cdot)$ 的选取等。
1.4. 反向传播
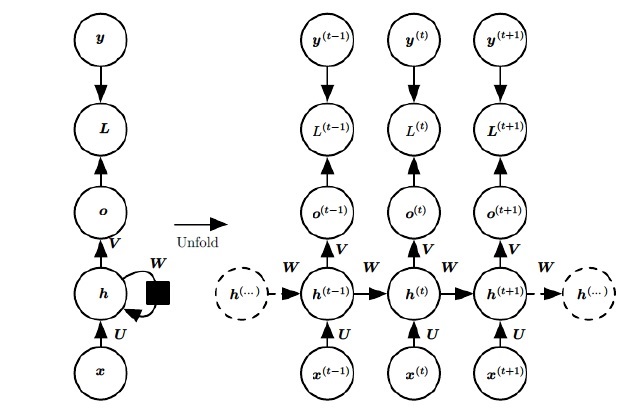
有了RNN前向传播算法的基础,就容易推导出RNN反向传播算法的流程了。RNN 反向传播算法的思路和 DNN 是一样的,即通过梯度下降法一轮轮的迭代,得到合适的RNN模型参数 $\boldsymbol U,\boldsymbol W,\boldsymbol V,\boldsymbol b,\boldsymbol c$。由于我们是基于时间反向传播,所以 RNN 的反向传播有时也叫做 BPTT (back-propagation through time)。当然这里的 BPTT 和 DNN 的 BP 也有很大的不同点,即这里所有的 $\boldsymbol U, \boldsymbol W,\boldsymbol V,\boldsymbol b,\boldsymbol c$ 在序列的各个位置是共享的,反向传播时我们更新的是相同的参数。
RNN反向传播过程中,需要计算 $\boldsymbol U,\boldsymbol W,\boldsymbol V,\boldsymbol b,\boldsymbol c$ 等参数的梯度。清晰起见,我们将前向传播过程整理如下
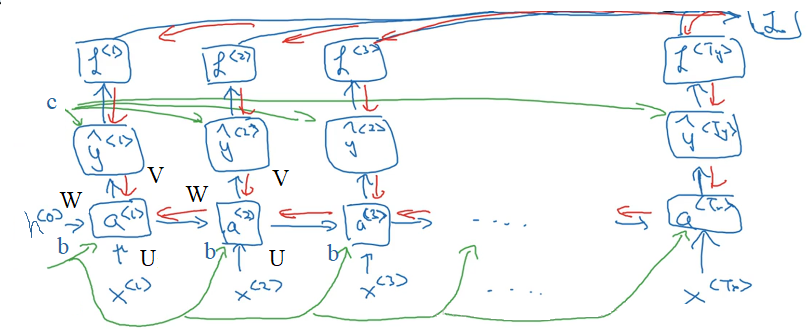
\[\begin{aligned} \boldsymbol a_t &= \boldsymbol W \boldsymbol h_{t-1} + \boldsymbol U \boldsymbol x_t + \boldsymbol b\\ \boldsymbol h_t &= f(\boldsymbol a_t)\\ \boldsymbol o_t &= \boldsymbol V \boldsymbol h_t + \boldsymbol c\\ \hat{\boldsymbol y_t} &= g(\boldsymbol o_t) \end{aligned}\]反向传播的形象的分析如下图所示。途中绿线是正向传播过程,红线是反向传播过程。可以看出,在输出端的 $V,c$ 参数仅与 $t$ 时刻的反向传播通路有关,因此分别求导数后求和即可。而输入端 $U,W,b$ 参数的梯度受到两个反向传播通路的影响,分别是 $t$ 时刻的输出端反向通路,以及 $t+1$ 时刻隐层信息的反向通路。
为了简化描述,这里的损失函数我们为交叉熵损失函数,输出的激活函数 $g(\cdot)$ 为 softmax 函数。对于 RNN,由于在序列的每个位置(任意 $t$ 时刻)都有输出 $\hat y_t$,也即都有损失函数,因此最终损失 $L$ 为
\[\boldsymbol L = \sum_{t=1}^T \boldsymbol L_t = \sum_{t=1}^T \left[ - \boldsymbol y_t ln\hat{\boldsymbol y_t} \right]\]注意到,对于任意时刻 $t$ 的损失函数 $\boldsymbol L_t$,在 $N$ 分类问题中其与每个维度分量均有关,因此损失函数可以进一步写为
\[\boldsymbol L = \sum_{t=1}^T \boldsymbol L_t = -\sum_{t=1}^T\sum_{j=1}^N y_{tj}{\rm ln} \hat{y_{tj}}\]上式就是负对数似然函数的形式。
首先计算比较简单的 $V,c$ 的梯度。在输出端的 $V,c$ 参数仅与 $t$ 时刻的反向传播通路有关,因此分别求导数后求和即可,有[1]
\[\begin{aligned} \frac{\partial L}{\partial \boldsymbol c} &= \sum_{t=1}^T \frac{\partial \boldsymbol L_t}{\partial \boldsymbol c} = \sum_{t=1}^T \frac{\partial \boldsymbol L_t}{\partial \hat{\boldsymbol y_t}} \frac{\partial \hat{\boldsymbol y_t}}{\partial \boldsymbol o_t} \frac{\partial \boldsymbol o_t}{\partial \boldsymbol c}\\ &= \sum_{t=1}^T -(\frac{\boldsymbol y_t}{\hat{\boldsymbol y_t}})\cdot softmax'\cdot \boldsymbol I\\ \end{aligned}\]由于 $softmax’$ 需要分情况讨论,当 $j=i$ 时 $softmax’ = \hat y_j(1-\hat y_j)$;当 $j\neq i$ 时 $softmax’ = \hat y_j\hat y_i$,那么有
\[\begin{aligned} \frac{\partial L}{\partial \boldsymbol c} &= \sum_{t=1}^T \sum_{j=1}^N -\frac{y_{tj}}{\hat y_{tj}}\cdot \left\{\begin{matrix} &\hat y_{tj}(1-\hat y_{tj})\quad &j=i\\ &\hat y_{tj}\hat y_{ti} \quad & j\neq i \end{matrix}\right.\\ &= - \sum_{t=1}^T \sum_{j=1}^N \left\{\begin{matrix} &y_{tj}(1-\hat y_{tj})\quad &j=i\\ &y_{tj}\hat y_{ti} \quad & j\neq i \end{matrix}\right.\\ \end{aligned}\]由于 $\boldsymbol y_{t} = [y_{t1},y_{t2},…,y_{tj},…,y_{tN}]$ 是一个 one-hot 向量,假设第 $j$ 个分量 $y_{tj} = 1$,可以将第二个累加符号消去(因为其它分量为 0,不影响累加求和)
\[\begin{aligned} \frac{\partial L}{\partial \boldsymbol c} &= - \sum_{t=1}^T \left\{\begin{matrix} &[0,0,...,y_{tj}(1-\hat y_{tj}),...,0]\quad &j=i\\ &[0,0,...,y_{tj}\hat y_{ti},...,0] \quad & j\neq i \end{matrix}\right.\quad (y_{tj} = 1) \end{aligned}\]进一步分析
- $j=i:\quad y_{tj}(1-\hat y_{tj}) = 1-\hat y_{tj} = y_{tj} - \hat{y_{tj}}$
- $j\neq i:\quad y_{tj}\hat y_{ti} = \hat y_{ti} = y_{tj} - \hat{y_{tj}}$
可以发现,二者在形式上可以写成统一的形式 $\boldsymbol y_{tj} - \hat {\boldsymbol y_{tj}}$,那么有
\[\begin{aligned} \frac{\partial L}{\partial \boldsymbol c} = - \sum_{t=1}^T (\boldsymbol y_{tj} - \hat {\boldsymbol y_{tj}}) =\sum_{t=1}^T (\hat {\boldsymbol y_{tj}} - \boldsymbol y_{tj}) \end{aligned}\]那么对 $\boldsymbol V$ 的偏导为
\[\begin{aligned} \frac{\partial L}{\partial V} &= \sum_{t=1}^T \frac{\partial L_t}{\partial c} = \sum_{t=1}^T \frac{\partial \boldsymbol L_t}{\partial \hat {\boldsymbol y_t}} \frac{\partial \hat {\boldsymbol y_t}}{\partial \boldsymbol o_t} \frac{\partial \boldsymbol o_t}{\partial \boldsymbol V}\\ &= \sum_{t=1}^T (\hat {\boldsymbol y_t}-\boldsymbol y_t)\boldsymbol h_t \end{aligned}\]$\boldsymbol U,\boldsymbol W,\boldsymbol b$ 的梯度计算就比较复杂了,误差传播源来自于两个反向传播通路的方向,分别是 $t$ 时刻的输出端反向通路,以及 $t+1$ 时刻隐层信息的反向通路。这里假设隐藏层的激活函数 $f(\cdot)$ 为 tanh 函数。
在进一步求解前,首先要考虑矩阵对向量求导的布局。根据布局约定(layout conventions),谁是列向量就是什么布局[2]:
- 分子布局(numerator layout): 分子为列向量且分母为行向量
- 分母布局(denominator layout):分子为行向量且分母为列向量
二者使用完全依据习惯而定,二者结果之间差一个转置。这里讨论了两种布局下的优劣。
如果我们采用分母布局(点此参考),即分母保持列向量,分子按行向量展开,那么有
\[\begin{aligned} \frac{\partial \boldsymbol {Ax}}{\partial \boldsymbol x} &= \partial \begin{bmatrix} A_{11} &A_{12}&\cdots&A_{1n}\\ A_{21} &A_{22}&\cdots&A_{2n}\\ \vdots &\vdots&\ddots&\vdots\\ A_{m1} &A_{n2}&\cdots&A_{mn}\\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2\\ \vdots\\ x_n\\ \end{bmatrix} / \partial \boldsymbol x\\ &= \begin{bmatrix} \partial (A_{11}x_1 + A_{12} x_2 + \cdots + A_{1n} x_n) & \cdots & \partial (A_{m1}x_1 + A_{m2} x_2 + \cdots + A_{mn} x_n)\\ \end{bmatrix}/\partial \boldsymbol x\quad <row!>\\ &= \begin{bmatrix} \partial (A_{11}x_1 + A_{12} x_2 + \cdots + A_{1n} x_n)/\partial \boldsymbol x & \cdots & \partial (A_{m1}x_1 + A_{m2} x_2 + \cdots + A_{mn} x_n)/\partial \boldsymbol x\\ \end{bmatrix}\\ &= \begin{bmatrix} \partial (A_{11}x_1 + A_{12} x_2 + \cdots + A_{1n} x_n)/\partial x_1 & \cdots & \partial (A_{m1}x_1 + A_{m2} x_2 + \cdots + A_{mn} x_n)/\partial x_1\\ \partial (A_{11}x_1 + A_{12} x_2 + \cdots + A_{1n} x_n)/\partial x_2 & \cdots & \partial (A_{m1}x_1 + A_{m2} x_2 + \cdots + A_{mn} x_n)/\partial x_2\\ \vdots & \cdots & \vdots\\ \partial (A_{11}x_1 + A_{12} x_2 + \cdots + A_{1n} x_n)/\partial x_n & \cdots & \partial (A_{m1}x_1 + A_{m2} x_2 + \cdots + A_{mn} x_n)/\partial x_n\\ \end{bmatrix}\\ &=\begin{bmatrix} A_{11} &A_{21}&\cdots&A_{m1}\\ A_{12} &A_{22}&\cdots&A_{m2}\\ \vdots &\vdots&\ddots&\vdots\\ A_{1n} &A_{2n}&\cdots&A_{mn}\\ \end{bmatrix} = \boldsymbol A^T \end{aligned}\]需要注意的是,分母布局下,求导的链式法则的顺序是反向的,假设 $\boldsymbol u = \boldsymbol u(\boldsymbol x)$,那么
\[\frac{\partial \boldsymbol f(\boldsymbol g(\boldsymbol u)}{\partial \boldsymbol x} = \frac{\partial \boldsymbol u}{\partial \boldsymbol x} \frac{\partial \boldsymbol g}{\partial \boldsymbol u} \frac{\partial \boldsymbol f}{\partial \boldsymbol g}\]我们先计算最后时刻 $t=T$ 的隐层梯度(分母布局链式法则方向相反)
\[\frac{\partial \boldsymbol L}{\partial \boldsymbol h_T} = \frac{\partial \boldsymbol o_T}{\partial \boldsymbol h_T} \frac{\partial \boldsymbol L}{\partial \boldsymbol o_T}\]前面求 $\boldsymbol V, \boldsymbol c$ 的梯度时已经求出
\[\frac{\partial \boldsymbol L}{\partial \boldsymbol o_T} = \frac{\partial \boldsymbol L}{\partial \hat {\boldsymbol y_T}}\frac{\partial \hat {\boldsymbol y_T}}{\partial \boldsymbol o_T} = \hat {\boldsymbol y_T}-\boldsymbol y_T = \nabla_{\boldsymbol o_T}\boldsymbol L\]假定 $\boldsymbol {Vh}_T$ 的结果是列向量,而 $\boldsymbol h_T$ 也是列向量,根据分母布局,有
\[\frac{\partial \boldsymbol L}{\partial \boldsymbol h_T} = \frac{\partial \boldsymbol o_T}{\partial \boldsymbol h_T} \nabla_{\boldsymbol o_T}\boldsymbol L = \frac{\partial \boldsymbol {Vh}_T}{\partial \boldsymbol h_T} \nabla_{\boldsymbol o_T}\boldsymbol L= \boldsymbol V^T\nabla_{\boldsymbol o_T}\boldsymbol L\]对于 $T$ 时刻之前的任意时刻 $t$,根据迭代关系,$\boldsymbol h_t$ 与 $\boldsymbol o_t$ 和 $\boldsymbol h_{t+1}$ 均有关,即
\[\begin{aligned} \boldsymbol h_{t+1} &= f(\boldsymbol a_{t+1}) =f(\boldsymbol W \boldsymbol h_t + \boldsymbol U \boldsymbol x_{t+1} + \boldsymbol b)\\ \boldsymbol o_t &= \boldsymbol V \boldsymbol h_t + \boldsymbol c\\ \end{aligned}\]对两个反向通路方向的梯度求和,有(分母布局链式法则方向相反)
\[\begin{aligned} \frac{\partial \boldsymbol L}{\partial \boldsymbol h_t}&=\frac{\partial \boldsymbol h_{t+1}}{\partial \boldsymbol h_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_{t+1}} + \frac{\partial \boldsymbol o_t}{\partial \boldsymbol h_t}\frac{\partial \boldsymbol L_t}{\partial \boldsymbol o_t}\\ &=\frac{\partial \boldsymbol h_{t+1}}{\partial \boldsymbol h_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_{t+1}} + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L \end{aligned}\]下面考察 $\partial \boldsymbol h_t / \partial \boldsymbol a_t$,因为 $\boldsymbol h_t, \boldsymbol a_t$ 均为列向量,若采用分母布局,将分子 $\boldsymbol h_t$ 看作行向量展开,那么
\[\begin{aligned} \frac{\partial \boldsymbol h_t }{ \partial \boldsymbol a_t} &= \partial[h_1,h_2,\cdots,h_D]/\partial \boldsymbol a_t\quad<row!>\\ &=\begin{bmatrix} \partial h_1/\partial a_1&\partial h_2/\partial a_1&\cdots&\partial h_D/\partial a_1\\ \partial h_1/\partial a_2&\partial h_2/\partial a_2&\cdots&\partial h_D/\partial a_2\\ \vdots&\vdots&\ddots&\vdots\\ \partial h_1/\partial a_D&\partial h_2/\partial a_D&\cdots&\partial h_D/\partial a_D\\ \end{bmatrix}\\ &= diag(f'(a_{t})) \end{aligned}\]其中 $diag$ 为对角线矩阵,因为下标不同的项偏导为 0 ,只有对角线元素非 0 。
若 $f(\cdot)$ 为 $tanh$ 函数,有 $tanh’=1-tanh^2$,那么
\[\frac{\partial \boldsymbol h_{t+1}}{\partial \boldsymbol a_{t+1}} = diag(tanh'(a_{t+1})) = diag(1-tanh(a_{t+1})^2) = diag(1-h_{t+1}^2)\]那么(分母布局链式法则反向)
\[\frac{\partial \boldsymbol h_{t+1}}{\partial \boldsymbol h_t} = \frac{\partial \boldsymbol a_{t+1}}{\partial \boldsymbol h_t} \frac{\partial \boldsymbol h_{t+1}}{\partial \boldsymbol a_{t+1}} = W^T diag(1-h_{t+1}^2)\]带回隐层梯度公式有
\[\frac{\partial \boldsymbol L}{\partial \boldsymbol h_t} = \boldsymbol W^T diag(1- h_{t+1}^2)\cdot\frac{\partial \boldsymbol L}{\partial \boldsymbol h_{t+1}} + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L\]稍作整理有
\[\nabla_{\boldsymbol h_t}\boldsymbol L = \boldsymbol W^T diag(1- h_{t+1}^2)\cdot\nabla_{\boldsymbol h_{t+1}}\boldsymbol L + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L\]可以看出,隐层梯度 $\nabla_{\boldsymbol h_t}\boldsymbol L$ 可以采用递归的方式求解。
下面即可写出 $\boldsymbol W,\boldsymbol U,\boldsymbol b$ 的梯度表达式(分母布局链式法则方向相反)
\[\begin{aligned} \frac{\partial \boldsymbol L}{\partial \boldsymbol b} &= \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol b}\frac{\partial \boldsymbol h_t}{\partial \boldsymbol a_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_t} = \sum_t \boldsymbol I\cdot diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L\\ \frac{\partial \boldsymbol L}{\partial \boldsymbol W} &= \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol W}\frac{\partial \boldsymbol h_t}{\partial \boldsymbol a_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_t} = \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol W}\cdot diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L\\ \frac{\partial \boldsymbol L}{\partial \boldsymbol U} &= \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol U}\frac{\partial \boldsymbol h_t}{\partial \boldsymbol a_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_t} = \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol U}\cdot diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L \end{aligned}\]对于 $\boldsymbol W$ 和 $\boldsymbol U$,需要进一步分析 $\boldsymbol a$ 对矩阵 $\boldsymbol W, \boldsymbol U$ 的偏导。因为
\[\boldsymbol a_t = \boldsymbol W \boldsymbol h_{t-1} + \boldsymbol U \boldsymbol x_t + \boldsymbol b\]以 $\boldsymbol a$ 对 $\boldsymbol W$ 的偏导为例,采用分母布局,即求导过程中的分母 $\boldsymbol W$ 保持为正常矩阵形式,而对分子中的 $\boldsymbol W \boldsymbol h$ 按行向量展开,有
\[\begin{aligned} &\frac{\partial \boldsymbol a}{\partial \boldsymbol W} = \frac{\partial \boldsymbol W \boldsymbol h}{\partial \boldsymbol W}=\partial \begin{bmatrix} w_{11}&w_{12}&\cdots&w_{1D}\\ w_{21}&w_{22}&\cdots&w_{2D}\\ \vdots&\vdots&\ddots&\vdots\\ w_{D1}&w_{D2}&\cdots&w_{DD} \end{bmatrix} \begin{bmatrix} h_1\\ h_2\\ \vdots\\ h_D \end{bmatrix}/ \partial \boldsymbol W\\ &=\begin{bmatrix} w_{11}h_1+w_{12}h_2+\cdots+w_{1D}h_D\\ w_{21}h_1+w_{22}h_2+\cdots+w_{2D}h_D\\ \vdots\\ w_{D1}h_1+w_{D2}h_2+\cdots+w_{DD}h_D\\ \end{bmatrix}^T/ \partial \boldsymbol W \quad <row!>\\ &=\begin{bmatrix} (w_{11}h_1+w_{12}h_2\cdots+w_{1D}h_D)/\partial w_{11}&(w_{21}h_1+w_{22}h_2\cdots+w_{2D}h_D)/\partial w_{12}&\cdots&(w_{D1}h_1+w_{D2}h_2\cdots+w_{DD}h_D)/\partial w_{1D}\\ (w_{11}h_1+w_{12}h_2\cdots+w_{1D}h_D)/\partial w_{21}&(w_{21}h_1+w_{22}h_2\cdots+w_{2D}h_D)/\partial w_{22}&\cdots&(w_{D1}h_1+w_{D2}h_2\cdots+w_{DD}h_D)/\partial w_{2D}\\ \vdots&\vdots&\ddots&\vdots\\ (w_{11}h_1+w_{12}h_2\cdots+w_{1D}h_D)/\partial w_{D1}&(w_{21}h_1+w_{22}h_2\cdots+w_{2D}h_D)/\partial w_{D2}&\cdots&(w_{D1}h_1+w_{D2}h_2\cdots+w_{DD}h_D)/\partial w_{DD} \end{bmatrix}\\ &=\begin{bmatrix} h_1&0&\cdots&0\\ 0&h_2&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&h_D \end{bmatrix}=diag (h^T) \end{aligned}\]对 $\boldsymbol U$ 的求导同理,最终有
\[\frac{\partial \boldsymbol a_t}{\partial \boldsymbol W} = diag(h_{t-1}^T) \quad\quad\quad \frac{\partial \boldsymbol a_t}{\partial \boldsymbol U} = diag(x_t^T)\]其中 $\boldsymbol h_t \in \mathbb R^D,\boldsymbol x_t \in \mathbb R^M$ 是列向量。
带入上面的$\boldsymbol W,\boldsymbol U,\boldsymbol b$ 的梯度表达式,有
\[\begin{aligned} \frac{\partial \boldsymbol L}{\partial \boldsymbol W} &= \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol W}\frac{\partial \boldsymbol h_t}{\partial \boldsymbol a_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_t} = \sum_t diag (h_{t-1}^T)\cdot diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L = \sum_t \cdot diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L \cdot \boldsymbol h_{t-1}^T\\ \frac{\partial \boldsymbol L}{\partial \boldsymbol U} &= \sum_t \frac{\partial \boldsymbol a_t}{\partial \boldsymbol U}\frac{\partial \boldsymbol h_t}{\partial \boldsymbol a_t}\frac{\partial \boldsymbol L}{\partial \boldsymbol h_t} = \sum_t diag (x^T)\cdot diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L = \sum_t diag(1-h_t^2)\nabla_{\boldsymbol h_t}\boldsymbol L \cdot \boldsymbol x^T \end{aligned}\]与参考链接 [6],[7] 的结果相同。最后将 $\boldsymbol h_{t-1}, \boldsymbol x_t$ 提到末尾的操作应该是成立的,懒得推导了…… 0.0
1.5. 梯度消失
RNN 存在时间维度上的梯度消失问题。
为了具体解释梯度消失的原因,首先将前面推导出来的 $t$ 时刻的 $\boldsymbol L$ 对隐层 $\boldsymbol h$ 的梯度递推过程列写如下
\[\nabla_{\boldsymbol h_t}\boldsymbol L = \boldsymbol W^T diag(1- h_{t+1}^2)\cdot\nabla_{\boldsymbol h_{t+1}}\boldsymbol L + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L\]注意到,$diag(1- h_{t+1}^2) = tanh(\boldsymbol h_{t+1})’$,那么上式可以改写为
\[\nabla_{\boldsymbol h_t}\boldsymbol L = \boldsymbol W^T tanh(\boldsymbol h_{t+1})'\cdot\nabla_{\boldsymbol h_{t+1}}\boldsymbol L + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L\]那么,对于 $t-1$ 时刻
\[\begin{aligned} \nabla_{\boldsymbol h_{t-1}}\boldsymbol L &= \boldsymbol W^T tanh(h_{t})'\cdot\nabla_{\boldsymbol h_{t}}\boldsymbol L + \boldsymbol V^T\nabla_{\boldsymbol o_{t-1}}\boldsymbol L\\ &=\boldsymbol W^T tanh(h_{t})'\cdot (\boldsymbol W^T tanh(\boldsymbol h_{t+1})'\nabla_{\boldsymbol h_{t+1}}\boldsymbol L + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L) + \boldsymbol V^T\nabla_{\boldsymbol o_{t-1}}\boldsymbol L\\ &=\boldsymbol W^T tanh(h_{t})'\cdot (\boldsymbol W^T tanh(\boldsymbol h_{t+1})'\nabla_{\boldsymbol h_{t+1}}\boldsymbol L + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L) + \boldsymbol V^T\nabla_{\boldsymbol o_{t-1}}\boldsymbol L\\ &=\boldsymbol W^T tanh(h_{t})'\cdot (\boldsymbol W^T tanh(\boldsymbol h_{t+1})'\cdots(\boldsymbol W^T tanh(\boldsymbol h_T)'\cdots) + \boldsymbol V^T\nabla_{\boldsymbol o_t}\boldsymbol L) + \boldsymbol V^T\nabla_{\boldsymbol o_{t-1}}\boldsymbol L\\ \end{aligned}\]稍微整理并展开,令 $\boldsymbol W^T tanh’(h) = WT$ 表示包含 $tanh’$ 的项,$\boldsymbol V^T \nabla_{\boldsymbol o}\boldsymbol L = \nabla$ 表示不含高阶次方的项,进行简化描述有(注意此处为简化描述,连乘表示为次方关系,略去了下标)
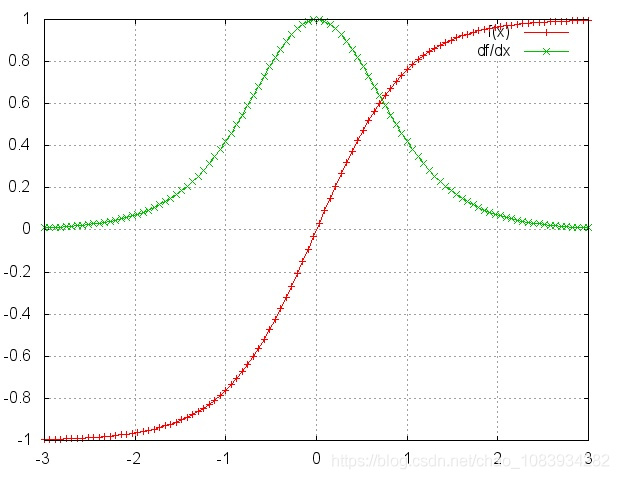
\[\begin{aligned} \nabla_{\boldsymbol h_{t-1}}\boldsymbol L &= (WT)^{T-t+1}\nabla_TL+(WT)^{T-t+2}\nabla+(WT)^{T-t+3}\nabla+...+(WT)^{1}\nabla+\nabla \end{aligned}\]而对 $tanh$ 及 $tan’h$ 进行画图如下
可以看出,由于 $tanh’$ 的值域在 $(0,1)$ 之间,对于训练过程大部分情况下 $tanh’$ 是小于 1 的。若 $\boldsymbol W^T$ 的取值较小导致 $WT = \boldsymbol W^T tanh’(h) <1$,多项连乘会导致最终的值趋近于0。因此,随着 $t$ 与 $T$ 的逐渐拉大,隐层梯度中包含的 $WT$ 项的次方越来越高,其取值越来越接近 0 。这会导致较长时间 $t$ 前的梯度项 $\nabla_{\boldsymbol h_{t-1}}\boldsymbol L$ 中的第一项十分接近 0 ,即导致较长时间 $t$ 前的 $\boldsymbol L$ 对参数的梯度项仅与那个时刻的输出有关(上式中的 $\nabla$ 项),而不再包含 $\boldsymbol L$ 的信息。
也就是说,在时间维度上较前时刻的权重无法根据最终的 loss 信息来更新。RNN 中参数的梯度被近距离梯度主导,导致模型难以学到远距离的依赖关系。
注意,RNN 中总的梯度是不会消失的。即便梯度越传越弱,那也只是远距离的梯度消失,由于近距离的梯度不会消失,所有梯度之和便不会消失。
RNN 梯度消失的本质:由于时间维度共享了参数矩阵,导致计算隐态 $\boldsymbol h_t$ 的梯度时会循环计算矩阵乘法,所以 BPTT 算法求解梯度时出现了参数矩阵的累乘,使得当时间尺度过长时的隐层梯度丢失。
1.6. 梯度爆炸
另一方面,若 $\boldsymbol W^T$ 的取值较大,导致 $\boldsymbol W tanh(\boldsymbol h)$ 的值大于1,那么连乘的每一项均大于1,就会导致梯度爆炸现象。
梯度爆炸会使得学习不稳定, 参数变化太大导致无法获取最优参数。
2. 参考文献
[1] 刘建平Pinard. 循环神经网络(RNN)模型与前向反向传播算法.
[2] 维基百科. 矩阵微积分-布局约定.
[3] 仙守. 数学-矩阵计算(4)两种布局.
[4] 谓之小一. LSTM如何解决RNN带来的梯度消失问题.
[5] thinkando. 机器学习中的矩阵、向量求导.
[6] Leo蓝色. RNN正向及反向传播.
[7] 小米粥. RNN的反向传播-BPTT.
[8] StatQuest. 【官方双语】全网最简单易懂的 [RNN循环神经网络] 介绍,一个视频理解梯度消失和梯度爆炸.