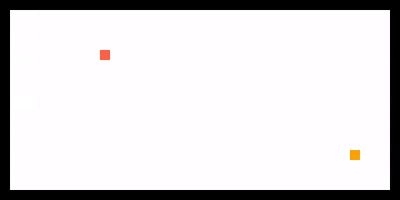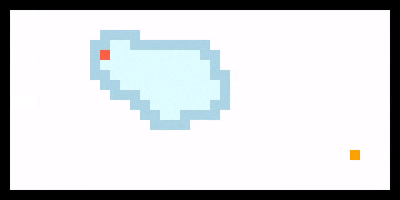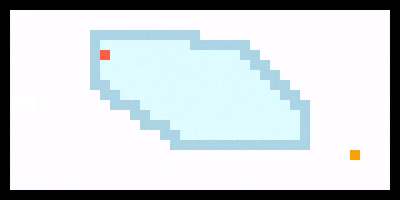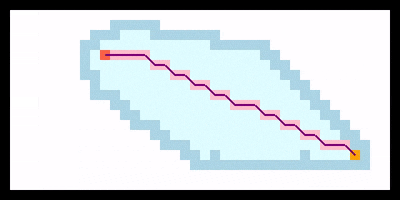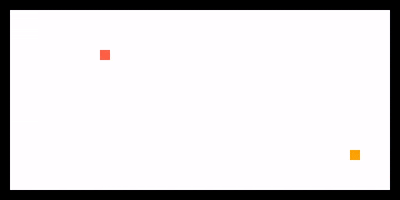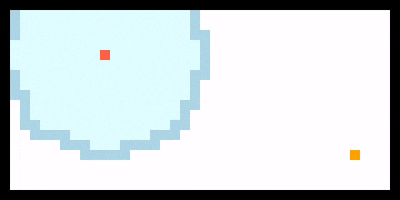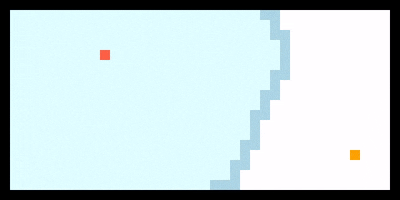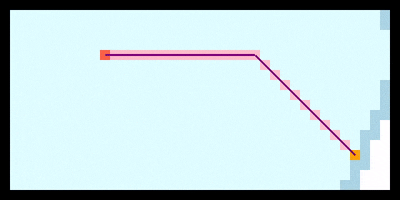首页 人工智能（搜索策略）
文章
取消

人工智能（搜索策略）

发表于 2025/09/17 更新于 2025/09/22
作者 sirlis
62 分钟阅读

搜索算法是人工智能领域的核心基础，为智能系统提供了在复杂问题空间中寻找可行解或最优解的能力。从简单的迷宫寻路到复杂的游戏决策，搜索算法构成了许多人工智能应用的基石。

本文系统性地介绍了人工智能中四大类搜索算法：无信息搜索、有信息搜索、$A^\star$ 搜索和蒙特卡罗树搜索。无信息搜索包括枚举搜索、广度优先搜索和深度优先搜索，它们不利用任何领域知识，通过系统性的空间探索来寻找解。有信息搜索则引入启发式函数来引导搜索方向，显著提高搜索效率，其中贪婪最佳优先搜索和A算法是典型代表。$A^\star$ 算法结合了 Dijkstra 算法的最优性保证和贪婪搜索的高效性，成为路径规划等领域的黄金标准。最后，蒙特卡罗树搜索通过随机模拟和树形搜索的结合，在复杂决策问题中展现出强大能力，特别是在 AlphaGo 等突破性 AI 系统中发挥了关键作用。

1. 概述

搜索是通过执行行为序列达到目标的工作，是由初始状态达到目标状态的求解过程。

在前面的知识表示和推理中，我们提到了正向推理和反向推理两种方法，并且提及 “不管是何种推理规则，在执行过程中都会得到不只一条规则被满足，此时推理机需要根据某种策略（如优先级、特异性、新近度等）选择一条规则来执行。” 这里的选择就是采取一种搜索策略。

根据搜索过程的不同，可以分几种搜索策略：

  • 无信息搜索策略
    • 广度优先搜索（Breadth-first search, BFS）
    • 深度优先搜索（Depth-first search, DFS）
  • 有信息搜索策略
    • 贪婪最佳优先搜索
    • $A^\star$ 搜索

2. 无信息搜索

无信息搜索又被称为盲目搜索，是预先规定好控制策略进行搜索，在搜索过程中获取的中间信息不影响或改变控制策略，由于搜索总是按预先规定的路线进行，没有考虑到问题本身的特性，所以这种搜索具有盲目性，效率不高，不便于复杂问题的求解。

尽管盲目搜索的性能不如启发式搜索，但由于启发式搜索需要抽取与问题本身有关的特征信息，而这种特征信息的抽取往往又比较困难，因此盲目搜索仍不失为一种有用的搜索策略。

2.1. 枚举搜索

枚举算法是我们在日常中使用到的最多的一个算法，它的核心思想就是：枚举所有的可能。枚举法的本质就是从所有候选答案中去搜索正确的解，使用该算法需要满足两个条件：

  • 可预先确定候选答案的数量；
  • 候选答案的范围在求解之前必须有一个确定的集合。

枚举算法简单粗暴，他暴力的枚举所有可能，尽可能地尝试所有的方法。虽然枚举算法非常暴力，而且速度可能很慢，但可以优先考虑，因为枚举法实现最简单，并且得到的结果总是正确的。

举例1：人生来就有三个生理周期，分别为体力、感情和智力周期，它们的周期长度为23天，28天，33天。每一个周期中有一天是高峰。已知三个生理周期高峰后分别经过了10天，12天，5天。问：下一次三个高峰落在同一天是第几天？

分析：

  • 可预先确定候选答案的数量；(1个)
  • 候选答案的范围在求解之前必须有一个确定的集合。（最多遍历 $23\times 28\times 33$ 次）为什么？

假设 $d$ 天后，三个高峰落在同一天。问题转化为如下同余方程：

\[\begin{aligned} d &\equiv 10 \pmod{23} \\ d &\equiv 16 \pmod{28} \\ d &\equiv 28 \pmod{33} \end{aligned}\]

其中 $a\equiv b \pmod c$ 的意思是 $a \mod c = b \mod c$，实际上上式可用中国剩余定理直接求解。无须枚举。

由于 $23$、$28$、$33$ 两两互质，根据中国剩余定理，同余方程组在模 $23\times 28\times 33 = 21252$ 下存在唯一解。

假设下一次人生巅峰时，三个高峰同为当天 $d$，经过 $n_1$ 个体力周期，$n_2$ 个感情周期，$n_3$ 个智力周期，有

\[d = 10+n_1\times 23 = 12+n_2\times 28 = 5+n_3\times 33\]

隐含要素： $n_1$，$n_2$，$n_3$ 都是整数！

则枚举搜索代码如下：

1
2
3
4
5

for(int t=1, t<23×28×33, t++)
{
  if ( (t-10)%23==0) && ((t-12)%28==0) && ((t-5)%33==0) )
    return t
}

举例2：有一个 $n\times m$ 方格的棋盘，问：其方格包含多少正方形、长方形（不包含正方形） ？

分析：

  • 可预先确定候选答案的数量；(有限个)
  • 候选答案的范围在求解之前必须有一个确定的集合。（很明显）
  • 矩形包含长方形和正方形，首先算出棋盘有多少个矩形

枚举边：

  • 一个矩形两个边，两点构成一个边
  • 横向所有可能的边长 $((n+1)\times n)/2$
  • 纵向所有可能的边长 $((m+1)\times m)/2$
  • 棋盘包含的所有的矩形个数为两式相乘。

正方形个数：

  • 正方形最大边长一定是m和n中的较小的那一个。
  • 假设正方形边长为 $i$，枚举 $i=1 \to i=\min(m,n)$
  • $i=1$ 时，正方形个数为 $m\times n$
  • $i=2$ 时，正方形个数为 $(m-1)\times (n-1)$
  • …

代码如下：

1
2
3
4
5
6
7
8

sum = (((n + 1) * n) / 2) * (((m + 1) * m) / 2);
for(int i = 1; i <= min(m, n); i++)
{
    square += x * y;
    x--;
    y--;
}
rec = sum - square;

2.2. 广度优先搜索

2.2.1. 搜索原理

广度优先搜索（Breadth-First Search, BFS）是一种用于遍历或搜索树或图数据结构的算法。它从根节点（或任意指定节点）开始，首先访问所有相邻节点，然后再依次访问这些相邻节点的未访问过的相邻节点。这个过程会逐层地向外扩展，因此它也被称为 “层次遍历”。

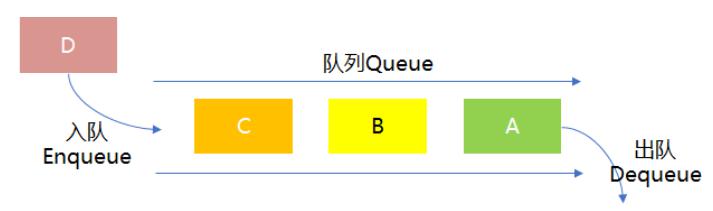
“先被访问的节点，其邻接点也先被访问”，这是一种先进先出（FIFO） 的思想。因此，BFS算法天然地需要借助队列（Queue） 这种数据结构来实现。

queue

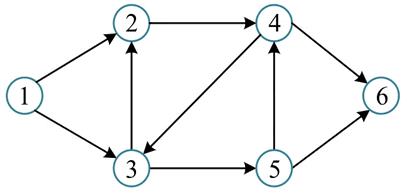
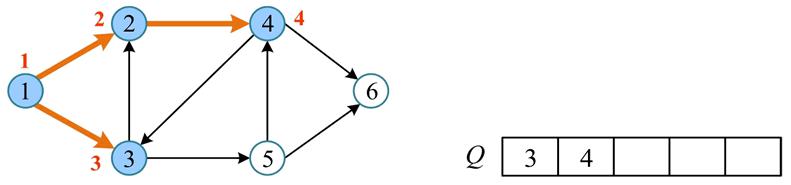
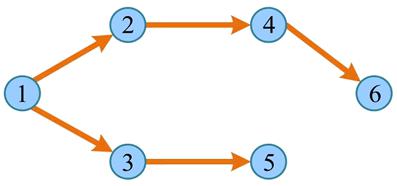
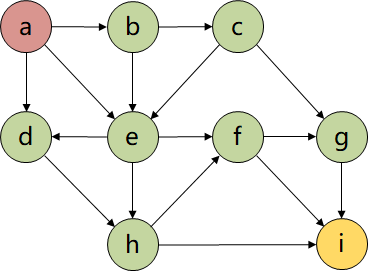
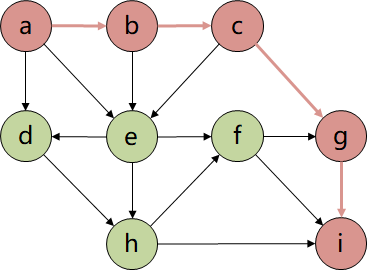
假设如下有向图，广度优先遍历过程如下所述：

bfs-0

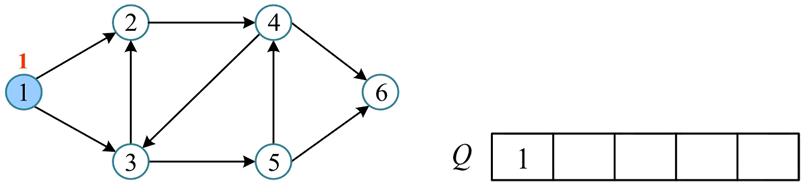
  1. 初始化所有节点的访问状态为未访问：visited[i] = false, i = 1, 2, 3, 4, 5, 6

  2. 创建一个空队列 $Q$，从任意节点出发（比如（1）），将节点（1）入队

bfs-1

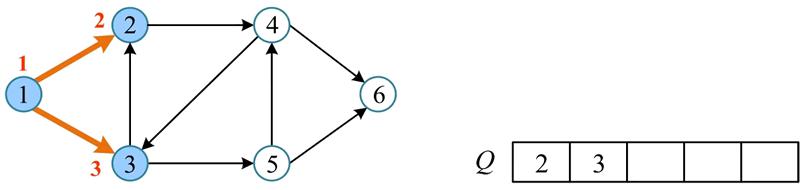
  1. 当队列 $Q$ 非空时，从队列中取出队首节点（1），并且标志 visited[1] = true。将取出节点的未被访问的邻接点（2、3）入队

bfs-2

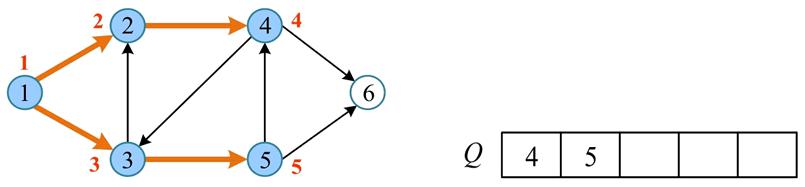
  1. 当队列 $Q$ 非空时，从队列中取出队首节点（2），并且标志 visited[2] = true。将取出节点的未被访问的邻接点（4）入队

bfs-3

  1. 当队列 $Q$ 非空时，从队列中取出队首节点（3），并且标志 visited[3] = true。将取出节点的未被访问的邻接点（5）入队

bfs-4

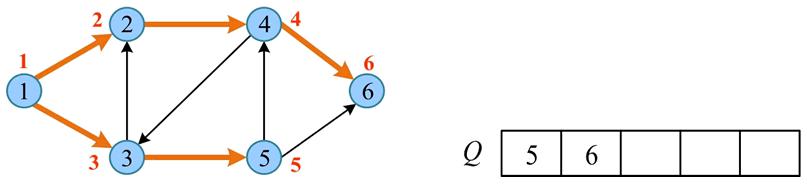
  1. 当队列 $Q$ 非空时，从队列中取出队首节点（4），并且标志 visited[4] = true。将取出节点的未被访问的邻接点（6）入队

bfs-5

  1. 当队列 $Q$ 非空时，从队列中取出队首节点（5），并且标志 visited[5] = true。取出节点的邻居节点均被访问。Q=[6]
  2. 当队列 $Q$ 非空时，从队列中取出队首节点（6），并且标志 visited[6] = true。取出节点的邻居节点均被访问。Q=[]
  3. 队列 $Q$ 为空，算法结束。广度优先遍历序列为 [1 2 3 4 5 6]。

广度优先遍历经过的节点及边形成的树被称为“广度优先生成树”，如下图所示。若广度优先遍历非连通图，则每个连通分量都会产生一棵广度优先生成树，所有广度优先生成树构成广度优先生成森林。

bfs-6

2.2.2. 代码实现

基于邻接矩阵的广度优先搜索代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

void BFS_AM(int s) {    // 基于邻接矩阵的广度优先遍历
    queue<int> Q;      // 创建一个普通队列（先进先出），存储 int 类型的数据
    cout<<s<<"\t";
    visited[s]=true;  // 标记为已访问
    Q.push(s);    // 将 s 入队
    while (!Q.empty()) {  // 若队列不为空
        int u=Q.front();  // 取出队头元素
        Q.pop();      // 队头元素出队
        for(int v=1;v<=n;v++) {  // 依次检查所有节点
            if (G[u][v] && !visited[v]) {  // u、v 邻接而且 v 未被访问
                cout<<v<<"\t";
                visited[v]=true;
                Q.push(v);
            }
        }
    }
}

遍历每个节点的邻接点的时间复杂度为 $O(n)$，共 $n$ 个节点，总时间复杂度为 $O(n^2)$。使用了一个辅助队列，每个节点都只入队一次，空间复杂度为 $O(n)$。

2.2.3. 搜索特点

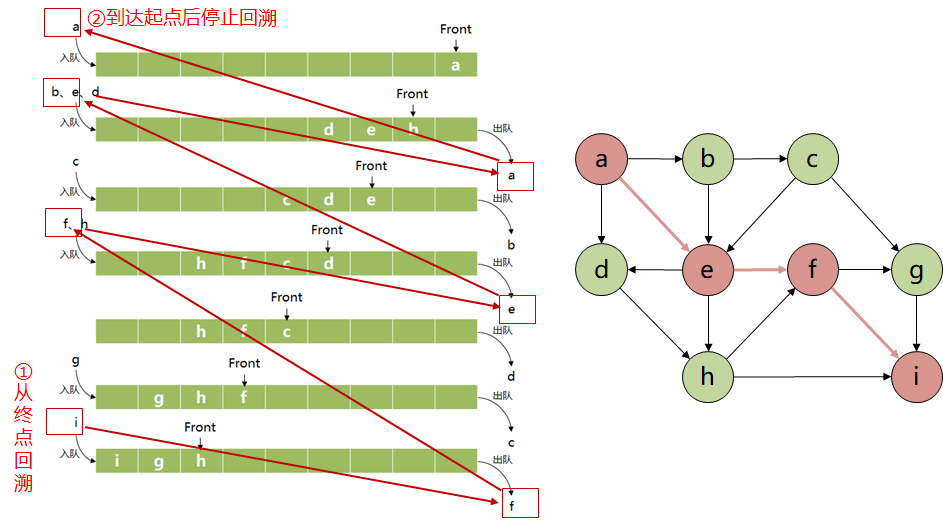
广度优先搜索能找到从起点到目标节点的最短路径，但它的最优性仅限于路径长度，而非其他优化目标。具体来说，当抵达终点时，从终点开始逐步回溯节点的父节点，最终抵达起点，得到的路径就是最短路径。

思考：广度优先搜索结束后如何回溯得到最优路径？

图中，从上至下是广度优先搜索的搜索过程，将搜索点入队，然后逐个取出队头的节点，并检查该节点的邻居节点，依次入队。当找到终点后，从终点回溯，找到它对应的父节点，并追溯到父节点入队时它的父节点，依次回溯直到起点。最终得到的路径就是最短路径。

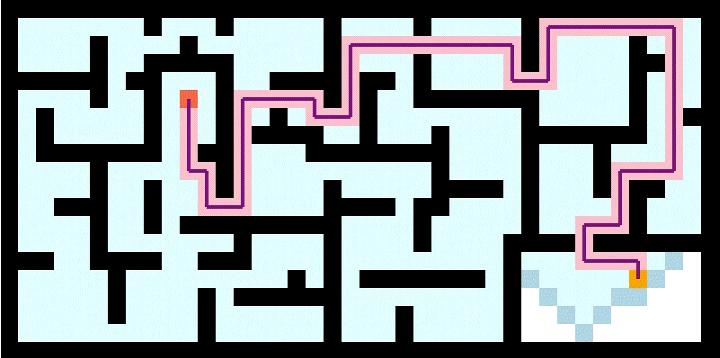
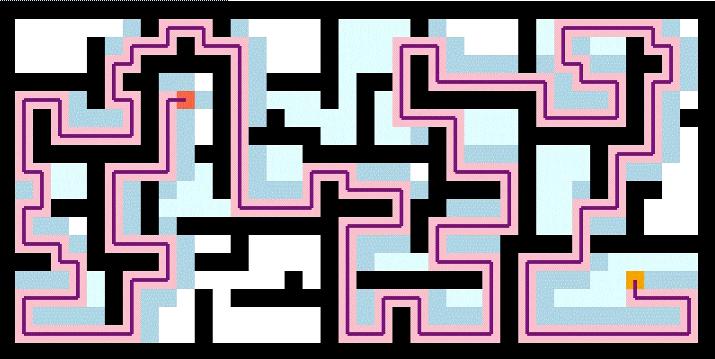
下图展示了一个使用广度优先搜索探索从迷宫起点到迷宫终点最短路径的例子：

可以看出，迷宫结束时，得到的路径确实是最短路径。

2.3. 深度优先搜索

2.3.1. 搜索原理

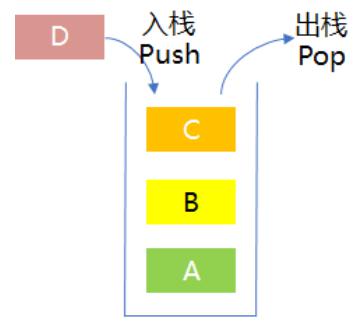
深度优先搜索（Depth-First Search）是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索一个分支，直到它到达尽头，然后回溯（Backtrack）到上一个分叉点，再选择另一条分支继续深入搜索。深度优先搜索使用递归或者栈（Stack）数据结构来实现上述特性。

栈是一种后进先出(LIFO)的容器，如下图

2.3.2. 代码实现

递归写法简洁，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <iostream>
#include <vector>
using namespace std;
void dfsRecursive(int node, vector<vector<int>>& graph, vector<bool>& visited) {
    // 1. 标记当前节点为已访问
    visited[node] = true;
    // 2. 处理当前节点（例如打印）
    cout << "Visiting node: " << node << endl;

    // 3. 递归地访问所有未访问的邻居
    for (int neighbor : graph[node]) {
        if (!visited[neighbor]) {
            dfsRecursive(neighbor, graph, visited);
        }
    }
}
// 主函数中调用示例
int main() {
    int numNodes = 5;
    vector<vector<int>> graph = { {1, 2}, {0, 3, 4}, {0}, {1}, {1} }; // 邻接表
    vector<bool> visited(numNodes, false); // 访问标记数组

    // 从节点0开始DFS遍历
    dfsRecursive(0, graph, visited);
    return 0;
}

而迭代的写法避免了递归深度过大的问题。因为递归使用系统的“调用栈”（Call Stack），而迭代使用自己申请的内存“栈”（Stack Data Structure）。系统调用栈的大小限制通常远小于我们自己在堆（Heap）上申请的栈数据结构的大小。因此，当递归深度非常大时，系统调用栈会先被耗尽，导致栈溢出（Stack Overflow）；而迭代法使用的堆内存空间通常大得多，更能处理深度大的问题。

迭代写法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

void dfsIterative(int start, vector<vector<int>>& graph, vector<bool>& visited) {
    stack<int> s;
    s.push(start);
    visited[start] = true;

    while (!s.empty()) {
        int currentNode = s.top();
        s.pop();
        cout << "Visiting node: " << currentNode << endl;

        // 注意：这里为了与递归顺序一致，从最后一个邻居开始压栈
        for (auto it = graph[currentNode].rbegin(); it != graph[currentNode].rend(); ++it) {
            int neighbor = *it;
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                s.push(neighbor);
            }
        }
    }
}

  • 时间复杂度：O(V + E)

    • V 是顶点（Vertex）的数量。

    • E 是边（Edge）的数量。

    • 原因：每个节点被访问一次（入栈/出栈一次），每条边也被检查一次（在遍历邻居时）。

  • 空间复杂度：O(V)

    • 最坏情况下，栈需要存储整条路径上的所有节点。例如，在一条链状的图中，栈可能同时存储所有V个节点。

    • 递归实现还需考虑系统调用栈的开销。

2.3.3. 搜索特点

尝试在下图中思考深度优先搜索的过程和结果（注意保持与递归顺序一致）

可以看出，深度优先搜索「**不能保证**」找到最短路径！

对于同样的迷宫例子，使用深度优先搜索算法，得到路径如下：

但是注意到，深度优先搜索的搜索速度更快，但找到的并不是最短路径。

2.4. 小结

深度优先搜索 能够快速地找到一条路径，是一种以时间换空间的方法，不能保证搜索到的路径是最优的。而 广度优先搜索 在搜索时呈波状推进形式，一路稳扎稳打，它是一种以时间换空间的方法，能够保证搜索到的路径是最优的。

3. 有信息搜索

广度优先搜索 和 深度优先搜索 的区别主要在于节点的弹出策略，根据弹出策略的区别，分别使用了队列和栈两种数据结构，而栈和队列作为两种相当基本的容器，只将节点进入容器的顺序作为弹出节点的依据，并未考虑目标位置等因素，这就使搜索过程变得漫无目的，导致效率低下。

启发式搜索（Heuristic Search）可以克服上述搜索效率低下的问题。启发式搜索是利用与问题相关的启发信息来预测目标节点的存在方向，并按该方向进行搜索，这样可以缩小搜索范围、提高搜索效率。

3.1. 启发信息与启发函数

  • 启发信息：与具体问题的求解过程有关的、并可指导搜索过程往最优希望方向前进的控制信息。启发信息主要包括以下三种信息：
    • 能有效帮助系统确定扩展节点的信息；
    • 能有效帮助决定哪些后继节点应该被生成的信息；
    • 能决定在扩展一个节点时哪些节点应从搜索树中删除的信息。
    - 思考：路径规划问题中有什么启发信息可以利用？ “两点之间的直线距离”就是一种启发信息。因为它告诉我们，当前点离目标点至少还有多远，这通常比“已经走过的路径长度”更能指导我们前进的方向。但 需要注意，诸如走迷宫等寻路问题中，直线路径可能与最短路径呈现冲突关系。
    - 思考：下棋游戏中有什么启发信息可以利用？ “棋盘上我方棋子数量减去对方棋子数量”或“控制中心区域的程度”就是一种启发信息。它能快速评估当前棋局对我方是否有利。
  • 启发函数：又称为估价函数，用于评估节点的重要性，是启发信息的数学化形式。它是一个具体的函数，用于量化评估从搜索树中的当前状态（或节点）到目标状态的 “期望距离” 或 “期望代价”。它通常记为 $h(n)$，其中 $n$ 代表当前节点。
    • 在搜索过程中，启发函数为每个待扩展的节点计算一个启发值，算法优先选择 “最有希望” 的节点（即 $h(n)$ 值最小的节点）进行扩展。
    • 既然 $h(n)$ 是一个估计值，那么它可能估计不准。启发函数不唯一，且的设计好坏直接影响搜索算法的优劣，最好的启发函数应与实际耗散相等。

“有信息搜索” 和 “启发式搜索” 的区别在于范畴的广度不同。所有的启发式搜索都是有信息搜索，但并非所有的有信息搜索都一定是启发式搜索。

有信息搜索的评估函数 $f(n)$ 可以是任何形式，而启发式搜索的 $f(n)$ 特指包含启发函数 $h(n)$ 的形式。

3.2. 贪婪最佳优先搜索

3.2.1. 搜索原理

如果我们设置评估函数就为启发函数：

\[f(n) = h(n)\]

其中 $h(n)$ 是从当前节点到目标节点的估计代价，这种策略被称为「贪婪最佳优先算法」（Greedy Best First Search, GBFS）。

对于当前节点 $n$ 和目标节点 $g$ ，常用的启发函数为欧氏距离和曼哈顿距离：

\[h(n) = \sqrt{(x_n - x_g)^2 + (y_n - y_g)^2}\] \[h(n) = |x_n - x_g| + |y_n - y_g|\]

3.2.2. 代码实现

GBFS 的算法流程和 BFS、DFS 并没有本质的不同，区别仍然在于采用的数据结构，GBFS 使用的是优先队列（Priority Queue），普通队列是一种先进先出的数据结构，而在优先队列中元素被赋予了优先级，最高优先级元素优先删除，也就是 first in, largest out 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>
using namespace std;

// 定义图结构（邻接表）
unordered_map<char, vector<pair<char, int>>> graph = {
    {'A', { {'B', 1}, {'C', 2} } },
    {'B', { {'D', 3} } },
    {'C', { {'E', 4} } },
    {'D', { {'F', 5} } },
    {'E', { {'F', 2} } },
    {'F', { } }
};

// 启发函数（每个节点到目标节点E的估计距离）
unordered_map<char, int> heuristic = {
    {'A', 8}, {'B', 5}, {'C', 6},
    {'D', 2}, {'E', 0}, {'F', 4}
};

vector<char> greedyBestFirstSearch(char start, char goal) {
    // 优先队列，按启发值h(n)排序（最小堆）
    priority_queue<pair<int, char>, vector<pair<int, char>>, greater<pair<int, char>>> frontier;
    frontier.push({heuristic[start], start});
    
    // 记录节点的父节点（用于重建路径）
    unordered_map<char, char> cameFrom;
    cameFrom[start] = '\0'; // 起始节点的父节点为空
    
    // 记录已访问的节点
    unordered_set<char> visited;
    visited.insert(start);
    
    while (!frontier.empty()) {
        // 获取当前h(n)最小的节点
        auto [current_h, current] = frontier.top();
        frontier.pop();
        
        cout << "扩展节点: " << current << " (h=" << current_h << ")" << endl;
        
        // 如果找到目标节点
        if (current == goal) {
            break;
        }
        
        // 遍历所有邻居
        for (auto& [neighbor, cost] : graph[current]) {
            if (visited.find(neighbor) == visited.end()) {
                int neighbor_h = heuristic[neighbor];
                frontier.push({neighbor_h, neighbor});
                cameFrom[neighbor] = current;
                visited.insert(neighbor);
                cout << "  添加邻居: " << neighbor << " (h=" << neighbor_h << ")" << endl;
            }
        }
    }
    
    // 重建路径
    if (cameFrom.find(goal) == cameFrom.end()) {
        return {}; // 未找到路径
    }
    
    vector<char> path;
    char current = goal;
    while (current != '\0') {
        path.push_back(current);
        current = cameFrom[current];
    }
    reverse(path.begin(), path.end());
    
    return path;
}

int main() {
    cout << "=== 贪婪最佳优先搜索 (GBFS) ===" << endl;
    cout << "从 A 到 E 的搜索过程:" << endl;
    cout << "==============================" << endl;
    
    vector<char> path = greedyBestFirstSearch('A', 'E');
    
    cout << "==============================" << endl;
    if (!path.empty()) {
        cout << "找到路径: ";
        for (int i = 0; i < path.size(); i++) {
            cout << path[i];
            if (i < path.size() - 1) cout << " -> ";
        }
        cout << endl;
    } else {
        cout << "未找到路径!" << endl;
    }
    
    return 0;
}

3.2.3. 搜索特点

GBFS 是极其 “目光短浅” 或 “贪婪” 的。它的策略非常简单：“哪个节点看起来离目标最近，我就下一步去哪”。它只关心未来，不关心过去。

将GBFS应用在二维地图路径规划中，如下图，可以看到它的指向性或者说目的非常明显，从起点直扑终点。

但是在实际的地图中，常常会有很多障碍物，它就很容易陷入局部最优的陷阱。下图的地图中有一个专门设置的局部最优陷阱，很显然GBFS虽然搜索速度够快，但是找不到最优路径。

将其应用到复杂二维地图路径规划中，效果如下：

3.3. A* 搜索

为了解决贪婪最佳优先搜索容易陷入局部最优的陷阱，A* 搜索引入了路径代价 $g(n)$ ，对应的评估函数设计如下所示：

\[f(n) = g(n) + h(n)\]

其中 ，$g(n)$ 是从初始节点到当前节点已经获知的实际代价，$h(n)$ 是从当前节点到目标节点的估计代价。

3.3.1. Dijkstra 算法

从初始节点到当前节点已经获知的实际代价 $g(n)$ 如何计算呢？

1959 年 Edsger W. Dijkstra（艾兹格·迪杰斯特拉）提出了著名的 Dijkstra 算法，是一种求解有权图中单个源点到所有其它节点的最短路径的算法。当被用于计算从源点到其它所有节点的最短路径时，正好能回答我们的上述问题。

  • 从某顶点出发，沿图的边到达另一顶点所经过的路径中，各边上权值之和最小的一条路径叫做最短路径。

  • 实际上，Dijkstra 本身就是单源最短路径算法，它运行完以后天然就得到了所有节点的 $g(n)$；$A^\star$ 只是在 Dijkstra 的骨架上再叠一个 $h(n)$ 来引导搜索方向。

  • 算法发展上，先有 Dijkstra（1959），后有 $A^\star$ （1968 由 Hart 等人提出）对 Dijkstra 做 “启发式加速”。所以有写教材上会先介绍 Dijkstra 算法，再介绍 $A^\star$ 算法。

Dijkstra 算法的前提条件为：图必须有非负权重。

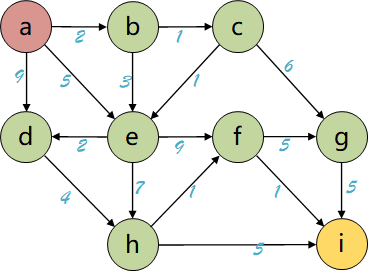
假设有如下图，想找到从 $A$ 到 $D$ 的最短路径。

graph LR;
A -- 6 --> B;
A -- 1 --> C;
C -- 2  --> B;
C -- 3 --> D;
B -- 5 --> D;

注意：Dijkstra算法使用优先队列（最小堆），总是先处理当前距离最小的节点，而不是按照添加顺序。因此算法处理过程如下表所示：

步骤 当前节点 距离表: A B C D 操作说明 优先队列内容 (距离,节点)
初始化 - [0, $\infty$, $\infty$, $\infty$] 起点A距离为0，其他为无穷大 [(0, A)]
1 A [0, 6, 1, $\infty$] 更新B(0+6=6)、C(0+1=1) [(1, C), (6, B)]
2 C [0, 3, 1, 4] 经C到B:1+2=3＜6，更新B；到D:1+3=4 [(3, B), (4, D)]
3 B [0, 3, 1, 4] 经B到D:3+5=8＞4，不更新D [(4, D)]
4 D [0, 3, 1, 4] 找到目标节点，算法结束 []

数学上可以证明：当所有边权非负时，当前距离最小的节点的距离值就是最终的最短距离。这是 Dijkstra 算法使用贪心选择扩展队列的关键。

尝试：使用 Dijkstra 算法计算起点 a 到终点 i 的最短路径。

此时再回顾并对比之前同一张图上的广度优先搜索和深度优先搜索结果，可以发现二者仅能处理无权图。

使用 Dijkstra 搜索算法走迷宫，由于迷宫并没有设置移动代价，所以其结果与广度优先搜索效果结果一致。

3.3.2. A* 算法

$A^\star$ 算法（A-Star Algorithm）是一种启发式搜索算法，由Peter Hart、Nils Nilsson和Bertram Raphael于1968年提出。它结合了 Dijkstra 算法的完备性和贪婪最佳优先搜索的效率。

A* 算法的评估函数设计如下所示：

\[f(n) = g(n) + h(n)\]

其中 ，$g(n)$ 是从初始节点到当前节点已经获知的实际代价，由 Dijkstra 算法计算得到 ；$h(n)$ 是从当前节点到目标节点的估计代价。

启发函数作为估计代价 $h(n)$，需要具备如下两个性质：

  • 可采纳性（Admissibility）：$h(n)$ 值必须小于等于从 $n$ 到目标节点的实际代价 $h(n) \leq h^\star(n)$，其中 $h^\star(n)$ 是从 $n$ 到目标节点的真实代价。

    • 永远不要高估到达目标的代价，启发函数必须是一个乐观的估计（低估代价）；

    • 在网格路径规划中，可采纳的启发函数就如前述提到的曼哈顿距离或欧几里得距离；

    • 可采纳性保证A*找到最优解。

    思考：如果使用不可采纳（非乐观估计）的启发函数会导致什么？ 可能找到次优解，完全错过最优解。 如下图，最优解为 $A\to B \to C$，代价 。 当走到节点 $B$ 时，真实 $h^\star(B)=1$； 若 $h(B)=8$ 则误导算法找到 ”最优解” 为 $A\to C$ 代价 10 
    graph LR
A -- 5 --> B
A -- 10 --> C
B -- 1 --> C

  • 一致性 (Completeness)：又被称为单调性。启发函数 $h(n)$ 是一致的，当且仅当对于图中任意节点 $n$ 和它的任一邻居 $n^\prime$，以及从 $n$ 到 $n^\prime$ 的代价 $c(n, n^\prime)$，满足以下条件：

    \[h(n) \leq c(n, n^\prime) + h(n^\prime)\]

    并且对于目标节点 $G$ 满足

    \[h(G) = 0\]
    • 一致性条件实际上就是数学中的三角不等式（可代入走迷宫等场景想象）；
    • 或者换个角度理解：启发函数的变化量（即坡度）应该小于真实代价（真实边权）；

    • 或者换个角度理解：估计变化不能超过实际变化；

    • 举例：想象一下实际的地理位置。从北京到上海的直线距离（$h(北京)$），一定小于或等于从北京到南京的实际距离（$c(北京, 南京)$）加上从南京到上海的直线距离（$h(南京)$）。

      \[h(北京) \leq c(北京, 南京) + h(南京)\]
    • 思考下面三个例子，判断是否满足一致性条件：
      • 认为餐厅还有1000米远。走了200米后，觉得还有700米远。

        不满足。$1000 \leq 200 + 700 \Rightarrow 1000 \leq 900$ 不满足一致性。一开始估计过于悲观保守了，估计远了。

      • 认为餐厅还有1000米远。走了200米后，觉得还有800米远。

        满足。一开始估计很准确。

      • 认为餐厅还有1000米远。走了200米后，觉得还有900米远。

        满足。一开始估计过于乐观了，认为自己距离餐厅比较近。

      • 认为餐厅还有1000米远。走了200米后，觉得还有1200米远。

        满足。虽然反直觉，感觉上”越走越远”很奇怪，但从数学上，一致性只要求逻辑自洽，不要求估计准确。初始估计 1000 米，走了 200 米后，认为还要 1200 米，这意味着你修正了之前的低估：原来 1000 米的估计太乐观了。虽然这样满足一致性，但启发函数质量很差，应该尽量设计启发函数，保证评估函数的变化与实际代价的变化方向一致且幅度合理。

    • 性质 1：如果一个启发式函数是一致的，那么它一定是可采纳的。一致性比可采纳性更强。
      • 思考：如何证明？ 假设我们要证明从任意节点 $n$ 到目标 $G$ 的估计 $h(n)$ 不大于实际代价 $h^\star(n)$。根据一致性，我们可以写出一系列不等式 \[\begin{aligned} h(n) &\leq c(n, n_1) + h(n_1)\\ & \leq c(n, n_1) + c(n_1, n_2) + h(n_2)\\ & \leq\cdots\\ & \leq c(n, n_1) + c(n_1, n_2) + c(n_2, n_3) + \cdots + h(G)\\ & =h^\star(n) \end{aligned}\]

    • 性质 2：一致性保证了评估函数 $f$ 的值单调不减，保证搜索过程是平稳的：

      \[\begin{aligned} f(n^\prime) &= g(n) + c(n, n^\prime) + h(n^\prime)\\ &= [g(n) + h(n)] + [c(n, n^\prime) + h(n^\prime) - h(n)]\\ &= f(n) + [c(n, n^\prime) - (h(n) - h(n^\prime))] \leq f(n) \end{aligned}\]

      这意味着 $A^\star$ 算法在扩展节点时，是沿着一个 $f(n)$ 值的等值面（或非递减前沿）进行扩展的。它第一次访问到一个节点时，所使用的路径就是到达该节点的最短路径（即 $g(n)$ 已经是最小的）。

3.3.3. 搜索流程

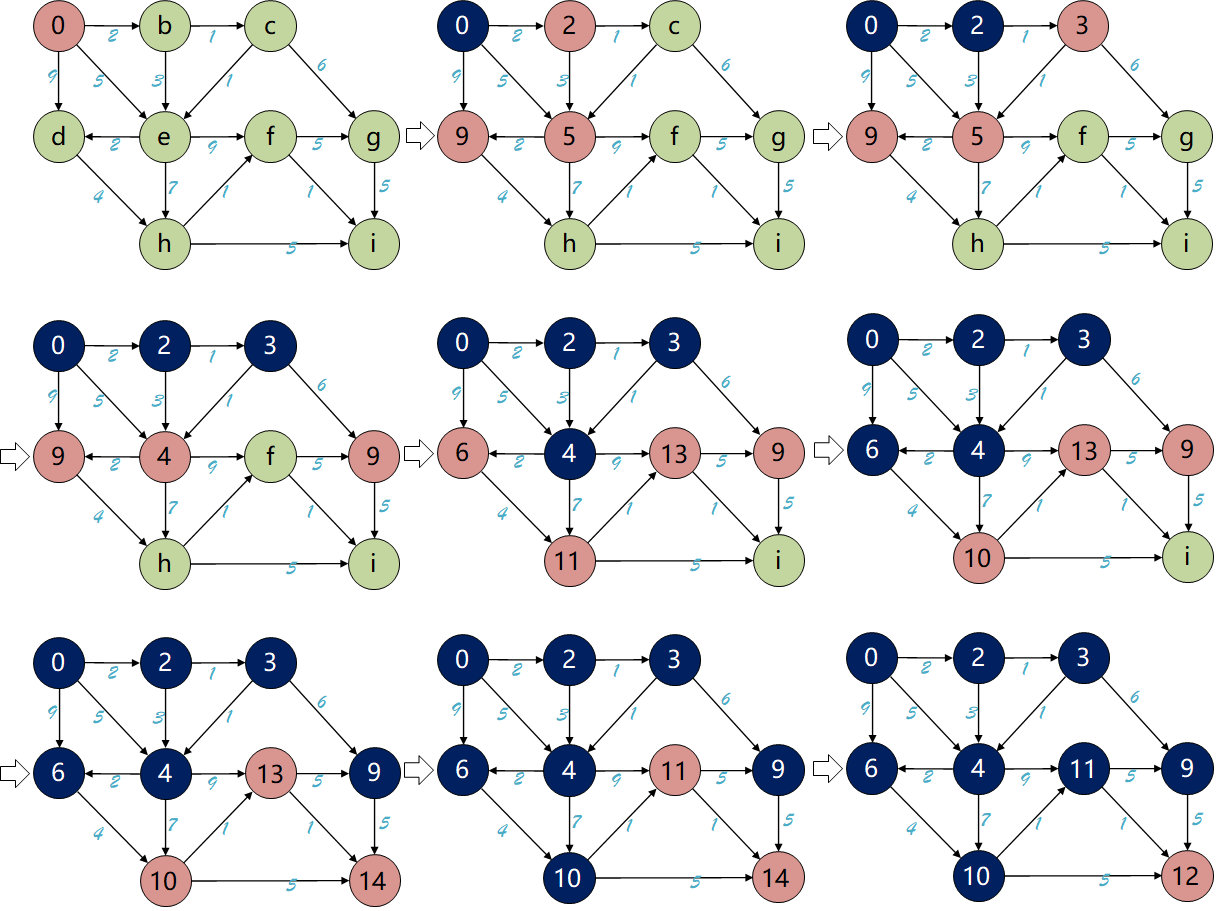
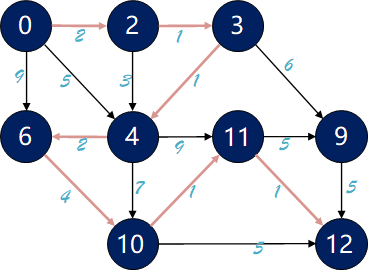
$A^\star$ 算法的搜索过程同样需要设置两个列表，分别为一个 open 列表和一个 close 列表。其中，open 列表保存已经生成但是还未处理的节点，close 列表保存已访问的节点。算法中每一步都需要根据评估函数重新排列 open 列表，这样循环中的每一步都只考虑 open 列表中的最小评估函数的节点。

以下面这个迷宫为例，演示 $A^\star$ 算法的搜索过程。其中绿色格子是起点，蓝色格子是障碍物，红色格子是终点。

具体步骤如下：

  • 从起点 S 开始，将 S 加入open 列表中，并设置其父节点为空；
  • 将 S 从 open 列表中弹出，移入 close 列表中；
  • 获取 当前节点 的所有邻接节点：
    • 判断其是否为终点、障碍物点、或已在 open 列表中：

      • 若都不是，则加入 open 列表，并计算邻接节点的评估函数 $f=g+h$ 值。简便起见，将评估函数、实际代价、启发函数分别列写在方格内特定位置。假设水平或垂直移动一格代价为 10, 斜向移动一格代价为 14，启发函数为曼哈顿函数，箭头指向父节点

      • 若邻接节点已经在 open 列表中，则重新计算评估函数 $f$ 值并根据情况更新；

  • 从 open 列表中选择评估函数 $f$ 最小的节点，并将其弹出，移入 close 列表中；

    • 返回上一步重复操作（触发了已经在 open 列表中的分支）；

      • 这里当前节点邻居均在 open 列表中，或为障碍物；
      • 对于 当前节点正上方的邻居，重新计算评估函数 $f$ 值；
      • 实际上是计算 $g$ 值，因为格子的 $h$ 值是不变的。
      • 黄色路径：当前节点代价为 $10$，纵向移动到上方邻居节点的代价为 $10$，合计代价为 $g=10+10=20$；
      • 蓝色路径：原始的 $g=14$；
      • $20 \leq 14$，导致新路径 $f$ 值更大，不更新；

      • 遍历所有邻居（红边框格子），完成上述操作；

  • 重复上一步，弹出 $f$ 值最小的节点（若有多个则随机选一个），并将其加入 close 列表中，并进行搜索、更新；

    • 假设随机选择了下方的节点作为当前节点；
    • 当前节点左侧的邻居已经在 open 列表中，计算后无须更新 $f$；

    • 当前节点下方的邻居移入 open 列表中，更新父节点，并计算 $f$；

  • 重复上一步，弹出 $f$ 值最小的节点

    • 此时当前节点为上方 $f=54$ 节点，与前述步骤镜像

  • 重复上一步，弹出 $f$ 值最小的节点
    • 此时当前节点随机选为下方 $f=60$ 节点，发现其正下方邻居节点在 open 表中

    • 计算 $g=20 < 28$，更新 $f=80$，更新父节点;

  • 算法结束的标志为：
    • 当前节点为终点，此时从终点回溯父节点，得到路径；
    • 遍历所有节点，但未找到终点；

3.3.4. 实例

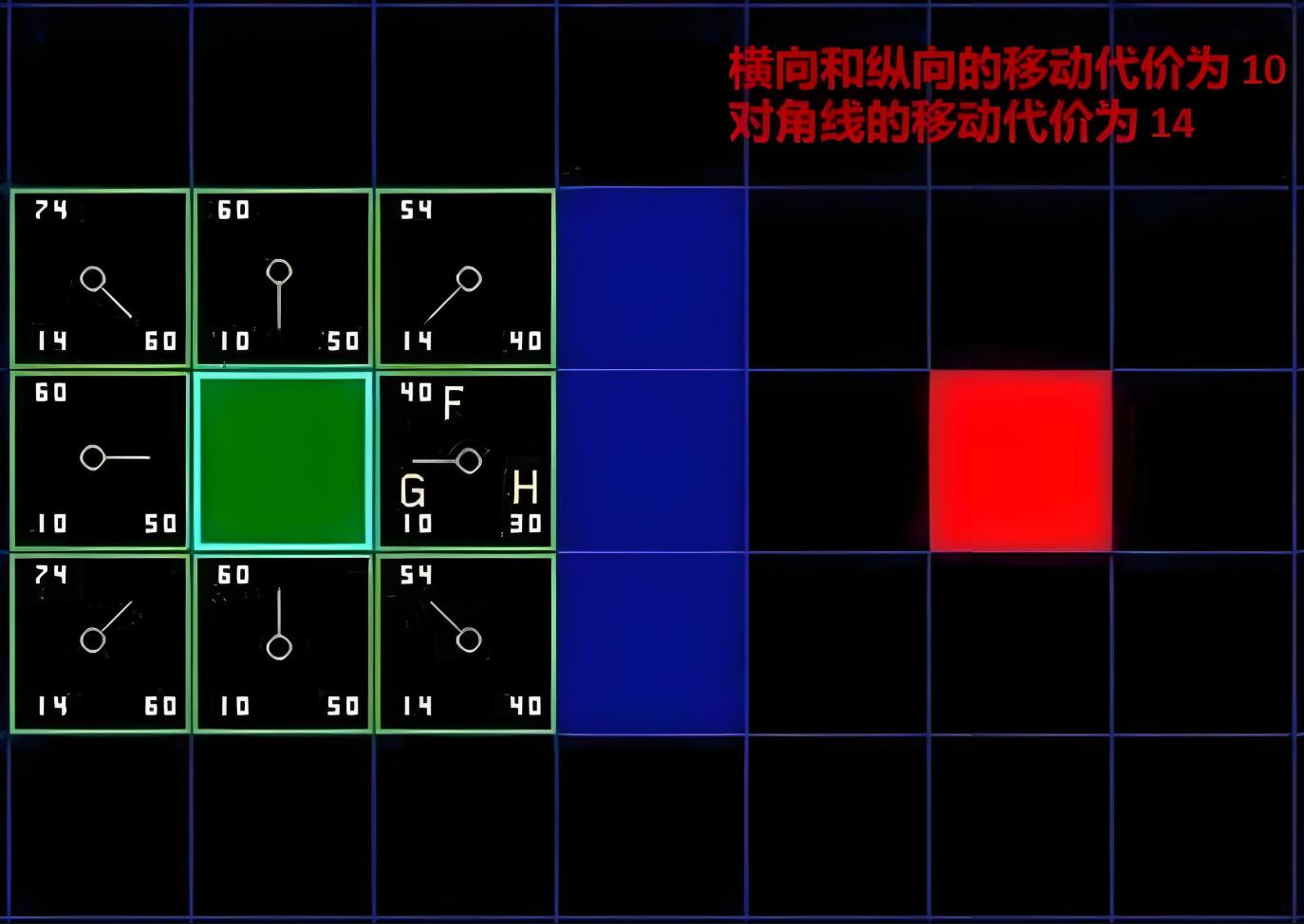
同样的无障碍场景，同样能够处理带权和斜向移动的算法，这里给出 Disktra 算法和 $A^\star$ 算法的比较：

4. 蒙特卡罗树搜索

4.1. 极大极小（minimax）搜索算法

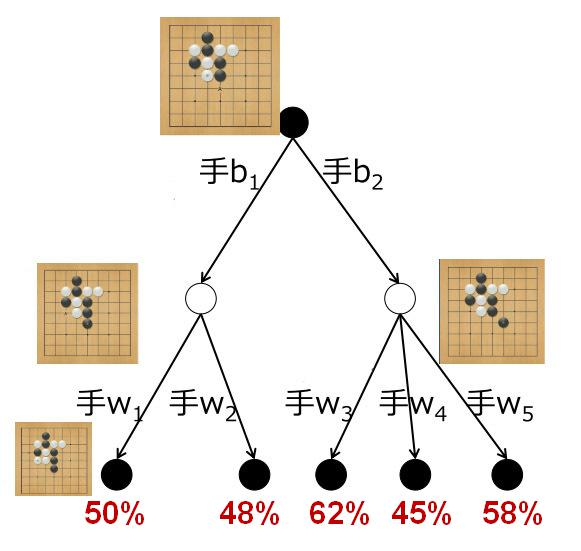
以围棋为例：

minimax

  • 轮到黑棋，黑棋有 $b_1$ 和 $b_2$ 两手可选，白棋对于 $b_1$ 有 $w_1$ 和 $w_2$ 两手可选，白棋对于 $b_2$ 有 $w_3, w_4 w_5$ 三手可选；
  • 如果白棋够聪明，会在黑棋走 $b_1$ 的时候回应以 $w_2$，在黑棋走 $b_2$ 的时候回应以 $w_4$。所以走 $b_1$ 后黑棋的真实胜率是 $48\%$，走 $b_2$ 后黑棋的真实胜率是 $45\%$；
  • 黑棋的正解是 $b_1$。这就是 minimax 搜索的核心思想：在搜索树中，每次轮到黑棋走时，走对黑棋最有利的；轮到白棋走时，走对黑棋最不利的。由于围棋是零和游戏，这就可以达到最优解；
  • 这是一个由底往上的过程：先把搜索树画到我们可以承受的深度且得到胜率评估，然后逐层往上取最大值或最小值回溯，就可以看到双方的正解。

如果想把 minimax 搜索运用到围棋上，立刻会遇到两个大问题：

  • 搜索树太广。棋盘太大了，每一方在每一步都有很多着法可选。
  • 搜索树太深，且很难评估胜率。除非把搜索树走到终局，这意味着要走够三百多步（因为对于电脑来说，甚至很难判断何时才是双方都同意的终局，所以只能傻傻地填子，一直到双方都真的没地方可以走为止）。简单地说，搜索树也需要特别深。

4.2. 蒙特卡罗树搜索

4.2.1. 蒙特卡罗方法

蒙特卡洛方法：也称统计模拟法、统计试验法。是把概率现象作为研究对象的数值模拟方法。是按抽样调查法求取统计值来推定未知特性量的计算方法。

蒙特卡罗是摩纳哥的著名赌城，该法为表明其随机抽样的本质而命名。故适用于对离散系统进行计算仿真试验。在计算仿真中，通过构造一个和系统性能相近似的概率模型，并在数字计算机上进行随机试验，可以模拟系统的随机特性。

通常采用蒙特卡罗方法求解的问题可以粗略地分成两类：

  • 一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机过程。例如在核物理研究中，分析中子在反应堆中的传输过程。中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。

  • 另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。

    • 比如计算任意函数的定积分：随机投点法、平均值法

4.2.2. 蒙特卡罗树搜索

1987 年 Bruce Abramson 在他的博士论文中提出了基于蒙特卡洛方法的树搜索（Monte Carlo Tree Search，MCTS）这一想法，是一种基于树数据结构、能权衡探索与利用、在搜索空间巨大仍然比较有效的的搜索算法。

MCTS 只适用于组合博弈（Combinatorial Game）的问题。

博弈论中，我们把零和、信息对称、确定性、离散、序列的游戏统称为 组合博弈。

  • 零和（zero-sum）：一方的收益必然意味着另一方的损失，收益和损失相加总和永远为零，故双方不存在合作的可能

  • 信息对称（perfect information）：游戏的所有信息、状态、规则都是所有玩家已知的；

  • 确定性（deterministic）：游戏终将结束，且有特定的判定规则判断输赢；

  • 离散（discrete）：博弈状态是有限的集合（如棋盘大小和落子位置）；

  • 序列（sequential）：博弈过程是序列进行的，双方轮流操作。

以取火柴游戏为例，有一堆 $n$ 个火柴，两人轮流从堆中取，每次取 $x$ 个（ $1 \leq x \leq n$），最后取光者为胜。或有若干堆火柴，两人轮流从中拿取，每次只能从一堆中取若干根，不可不取，最后取完者为胜。

以围棋为例，这类算法要解决的问题是这样的，我们把围棋的每一步所有可能选择都作为树的节点，第零层只有 1 个根节点，第 1 层就有 361 种下子可能和节点，第 2 层有 360 种下子可能和节点，这是一颗非常大的树，我们要在每一层树节点中搜索出赢概率最大的节点，也就是下子方法。

蒙特卡罗树搜索如何解决 之前 minimax 搜索算法应用于围棋领域的问题呢？

  • 搜索树太广：根据它的设计，搜索树会较好地自动集中到“更值得搜索的变化”（注意，也不一定准）。如果发现一个不错的着法，蒙特卡洛树搜索会较快地把它看到很深，可以说它结合了广度优先搜索和深度优先搜索，类似于启发式搜索。这就部分解决了第一个问题；
  • 搜索树太深，且很难评估胜率：它可以给出一个局面评估，虽然不准，但比没有强。这就部分解决了第二个问题。

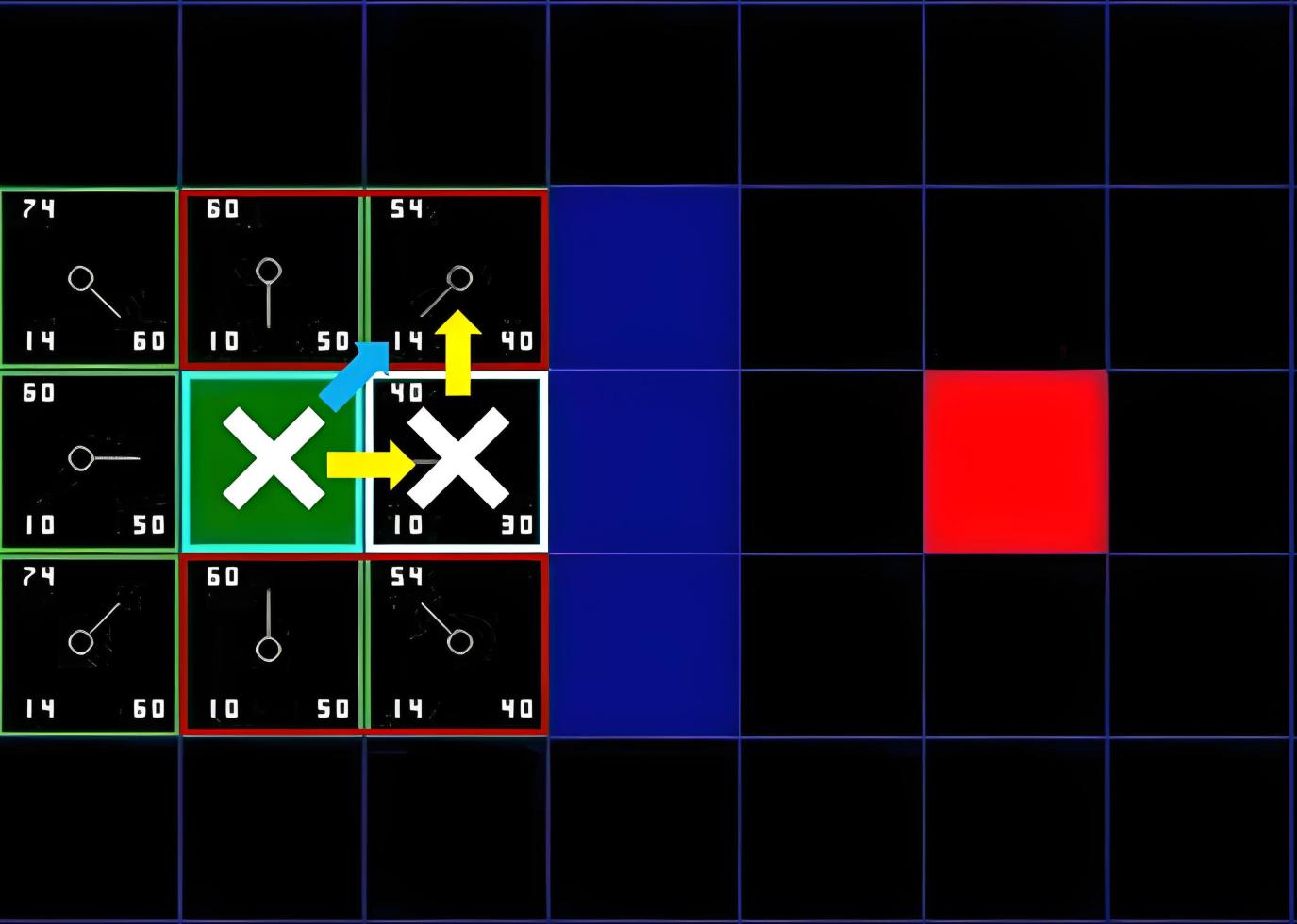
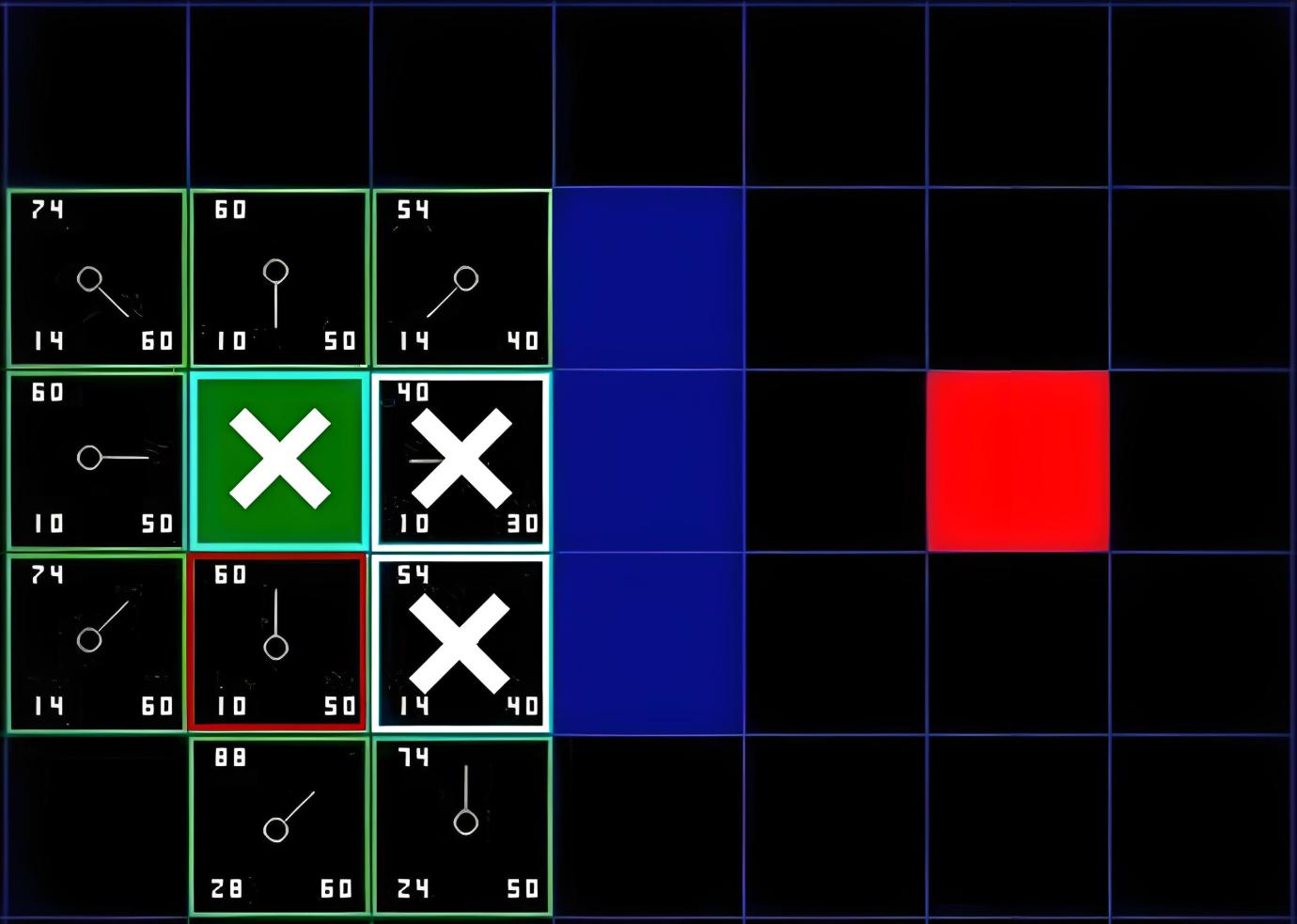
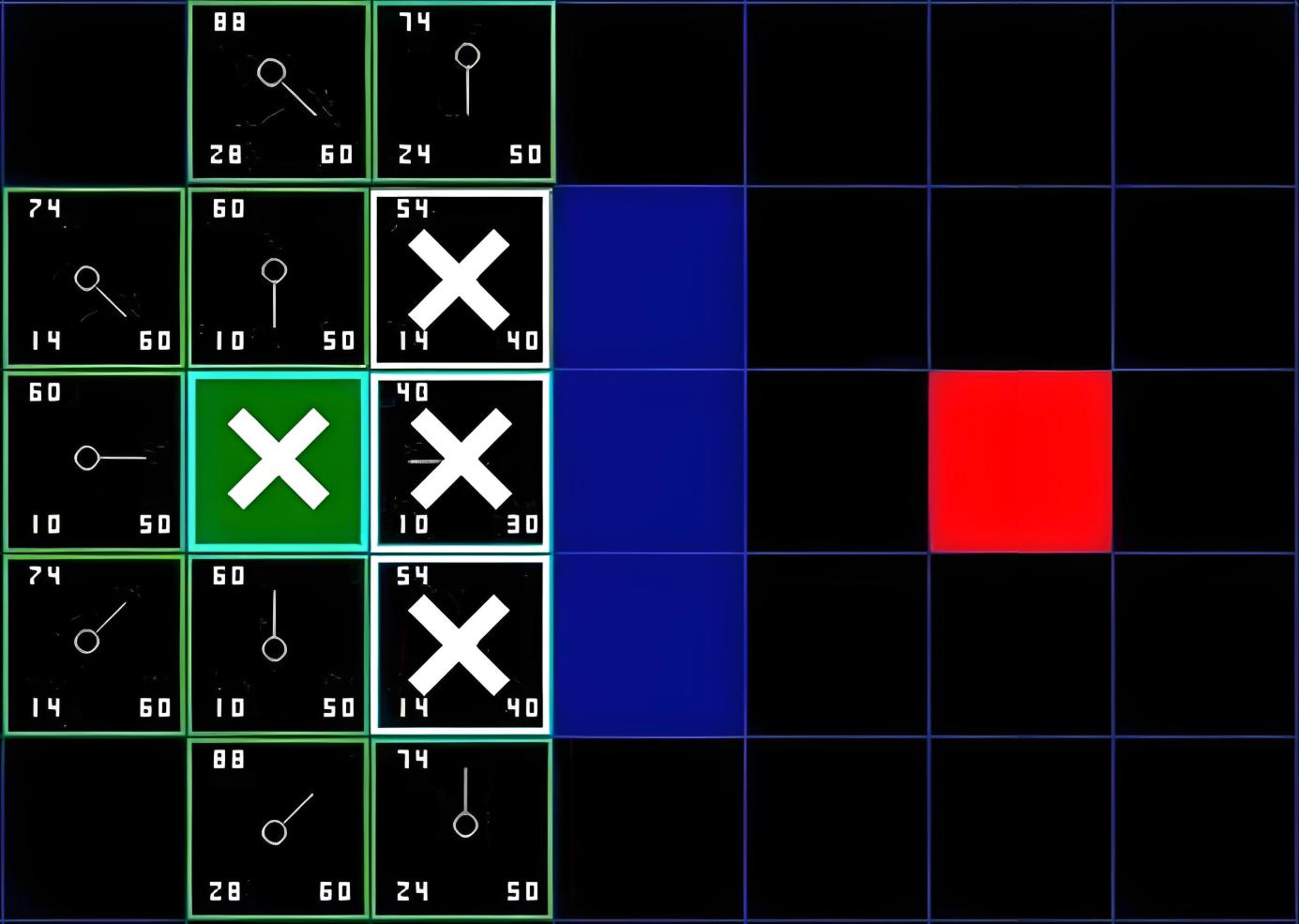
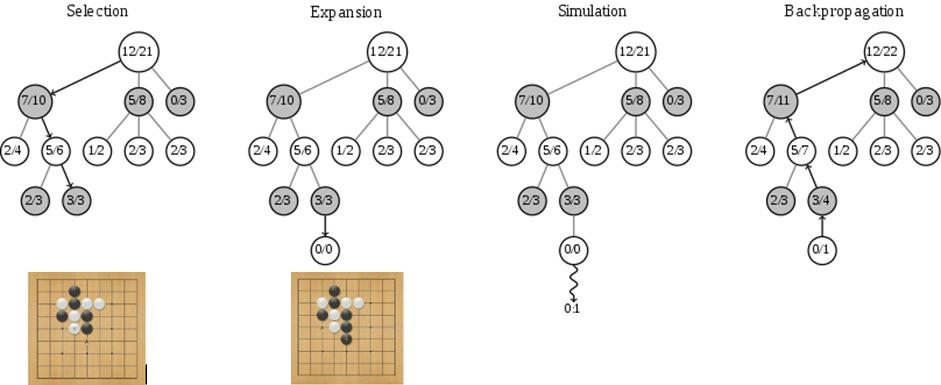
观察如下围棋对局的过程，图中每个节点代表一个局面。而 $x/y$ 代表这个节点被访问 $y$ 次，其中黑棋胜利了 $x$ 次。例如一开始的根节点是 $12/21$，代表总共模拟了 $21$ 次，黑棋胜利了 $12$ 次。

mcts-1

MCTS 的主要步骤是选择、扩展、模拟（评估）、回溯：

  • 选择（Selection）：从根节点往下走，每次都选一个 “最值得看的子节点”（具体规则稍后说），直到来到一个 “存在未扩展的子节点” 的节点，如图中的 $3/3$ 节点。“存在未扩展的子节点” 其实就是指这个局面存在未走过的后续走法；
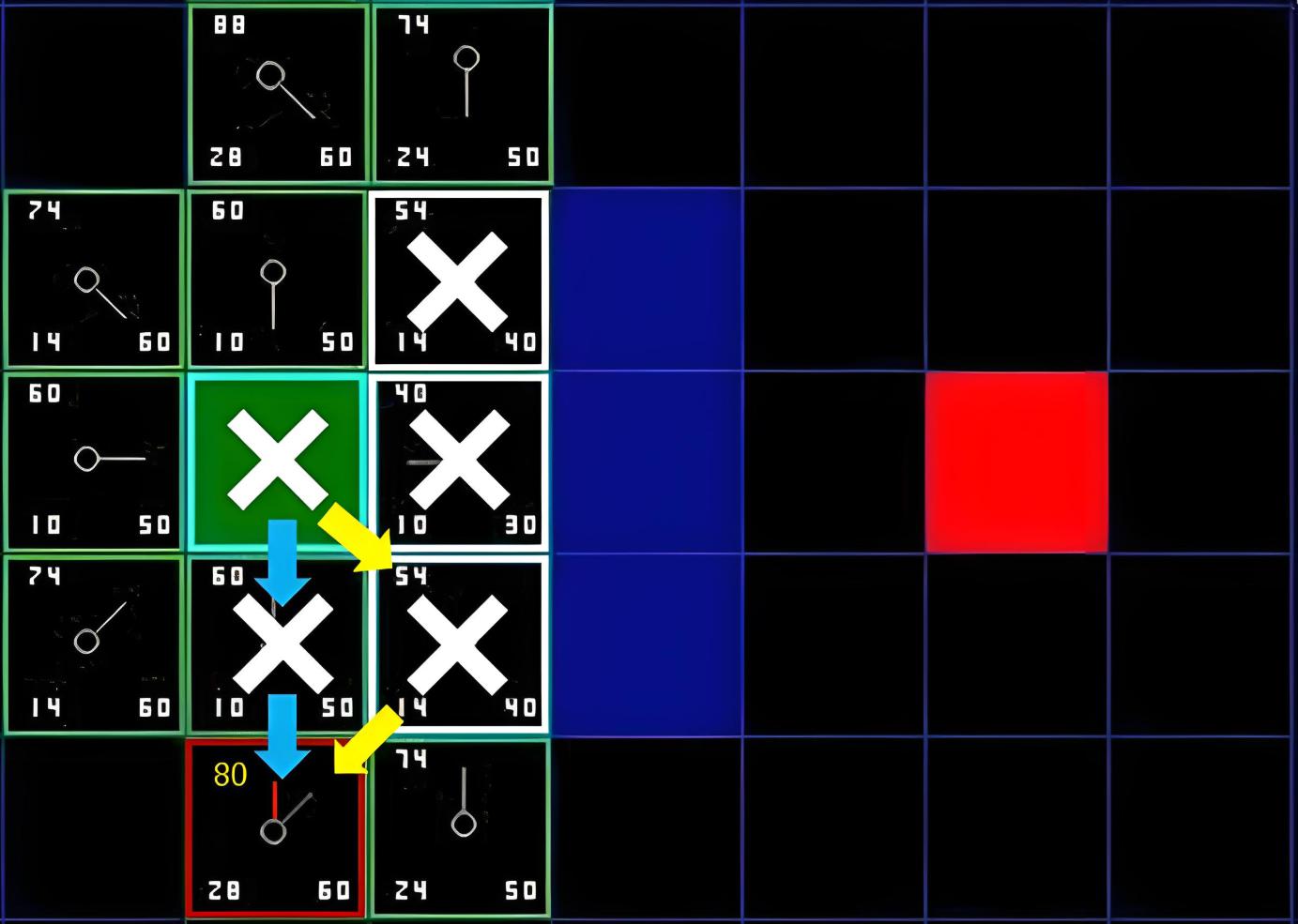
  • 扩展（Expansion）：给这个节点加上一个 $0/0$ 子节点，对应之前所说的 “未扩展的子节点”，就是还没有试过的一个着法。
  • 模拟（Simluation）：或称为评估。从没有试过的走法开始，用快速走子策略（Rollout policy）走到底，得到一个胜负结果。快速走子策略适合选择一个棋力很弱但走子很快的策略。因为如果这个策略走得慢，虽然棋力会更强，结果会更准确，但由于耗时多了，在单位时间内的模拟次数就少了，所以不一定会棋力更强，有可能会更弱。这也是为什么我们一般只模拟一次，因为如果模拟多次，虽然更准确，但更慢；
  • 回溯（Backpropagation），把模拟的结果加到它的所有父节点上。例如第三步模拟的结果是 $0/1$（代表黑棋失败），那么就把这个节点的所有父节点都加上 $0/1$。

我们回过头来分析选择过程，注意到前面提及需要选择一个 “最值得看的子节点”。假设对于一个局面（根节点），可供选择的情况有三种可能：

  • 该节点所有子节点都已经被扩展过
  • 该节点有子节点还未被扩展过
  • 这个节点游戏已经结束了
思考：用快速走子解决深度问题，那么能否用 minmax 选择 “最值得看的子节点” ？ 不能太贪心，不能每次都只选择 “最有利的/最不利的”，因为这会意味着搜索树的广度不够，容易忽略实际更好的选择。

MCTS 提出了一个选择策略，计算置信区间上界（Upper Confidence Bound，UCB）作为选择依据：

\[\text{UCB}(v_i, v) = \underbrace{\frac{x(v_i)}{y(v_i)}}_{利用} + \underbrace{c \times \sqrt{\frac{\log y(v)}{y(v_i)}}}_{探索}\]

其中，第一项计算了节点 $v_i$ 的平均胜率，胜率越高被选择的概率就应该越大；第二项表示对访问次数较少的节点的探索鼓励，若某个节点访问次数 $y(v_i)$ 比较少，则该项值越大。公式中的常数 $c$ 可以根据问题调整，一般取 $\sqrt{2}$。​

因此，若：

  • 该节点所有子节点都已经被扩展过

    • 使用 UCB 公式选择一个值最大的子节点继续向下搜索。

  • 该节点有子节点还未被扩展过

    • 转向扩展（Expansion） 步骤，扩展一个未访问的子节点。

  • 这个节点游戏已经结束了

    • 直接回溯游戏结果。

对于模拟（评估）步骤，引入了快速走子策略走到底，得到一个胜负结果，这里快速走子策略可以有多种选择：

  • 基于规则库的专家算法
  • 深度学习预训练模型
Academic, Knowledge
artificial intelligence
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容

人工智能（知识表示与推理）

-