首页 强化学习（策略梯度法）
文章
取消

强化学习（策略梯度法）

发表于 2023/11/27 更新于 2025/04/18
作者 sirlis
49 分钟阅读

本文介绍了强化学习的策略梯度法（Policy Gradient）。

1. 回顾基于价值的强化学习

基于价值函数的强化学习方法

  • 动态规划方法（Dynamic Programming, DP）
  • 蒙特卡洛方法（Monte Carlo, MC）
  • 时序差分方法（Temporal-Difference, TD）

这三种方法存在共同特点：

  • 在求解强化学习任务时，最终目标是求解满足规则的最优策略 $\pi$。但以上三种方法并 没有直接求解 策略 $\pi$ 这个变量，而是先计算状态价值函数 $v_\pi(s)$ 或状态-动作价值函数 $q_\pi(s,a)$；然后再基于价值函数结果改进策略 $\pi$，是一种间接方式;
  • 在策略改进过程中，本质上均选择最优价值函数对应的动作作为新的策略；
  • 均为表格式强化学习的代表方法。

特别地，对于 DQN 方法，神经网络的输入是原始的状态信息，如游戏画面，输出是在这种状态下执行各种动作的回报，即价值函数（Q函数）。训练完成之后，神经网络逼近的是最优 $q(s,a)$。

1
2
3

          +----+ ----> Q(s,a1)                       +----+
  s  ---> |f(x)| ----> Q(s,a2)       or     s,ai --->|f(x)| ----> Q(s,ai)
          +----+ ----> Q(s,a3)                       +----+

以 DQN 为代表的值函数近似方法，虽然在某些问题上取得了成功，但存在以下问题：

  • 无法表示随机策略。某些问题的最优策略是随机策略，需要以不同的概率选择不同的动作。而基于价值的强化学习算法在实现时采用了贪心策略，给定一个状态 ，选择的策略是确定性的，显然无法实现这种按照概率执行各种候选动作的要求。比如石头剪刀布的最优策略是以 (1/3, 1/3, 1/3）的概率来选择石头/剪刀/布，基于价值的强化学习无法实现这种策略。

  • 无法处理高维动作空间。DQN 要求动作空间是离散的，且只能是有限个，这样才能寻找使动作值函数最大化的动作的操作。但在很多问题特别是物理控制任务中，具有连续实值和高维的动作空间，例如要控制在 x y z 方向的速度、加速度。DQN 不能直接应用。

  • 难以收敛。基于价值的强化学习方法输出的价值（如各个动作的最优 Q 函数值）的微小改变会导致某一动作被选中或不选中，这种不连续的变化会影响算法的收敛。这很容易理解，假设一个动作a的Q函数值本来在所有动作中是第 2 大的，把它增加 0.0001，就变成最大的，那这种微小的变化会导致策略完全改变。因为之前它不是最优动作，现在变成最优动作了。

  • 存在徘徊。在观察受限的情况下，基于价值的强化学习方法会出现徘徊现象。即出现不同状态导致的观察相同，使得对应相同的 “最佳” 策略，但明显不符合任务实际情况的现象。

本质上，以 DQN 为代表的值函数近似方法，已经能够较好地将价值函数通过神经网络进行逼近，但最终进行策略选取时，还是只能适用于表格形式的离散策略。我们是否能够借鉴值函数近似方法，采用函数来直接近似策略呢？

2. 策略梯度

2.1. 策略函数

直接借鉴值函数近似的方法，使用神经网络作为策略函数，输出某个状态 $s$ 下执行各种动作的概率值，即将策略参数化为

\[\pi(a\vert s) = p(a \vert s;\theta)\]

这种做法的原理如下图所示

1
2
3
4

          +----+ ----> p(a1|s;θ)
  s  ---> |f(x)| ----> p(a2|s;θ)
          |  θ | ----> ...
          +----+ ----> p(a3|s;θ)

此时，动作 $a$ 服从某一概率密度函数 $p(a\vert s;\theta)$ ，也即将动作 $a$ 理解成从概率模型 $p(a\vert s;\theta)$ 产生的样本。我们的目标也就从直接求解 $p(a\vert s;\theta)$ 转换成求解参数 $\theta$。

将含参数 $\theta$ 的策略称为策略函数，记作 $\pi(a \vert s;\theta)$，通常情况下可简写成 $\pi_{\theta}$。

2.2. 策略函数的分布形式

前面假设动作 $a$ 服从某一概率密度函数 $p(a\vert s;\theta)$，这里对其概率密度函数形式进行一些额外的讨论。

  • 如果动作 $a$ 是离散随机变量，使用 $\text{softmax}$ 函数将其映射为 指数族分布

    这里并不是一定要使用 $\text{softmax}$ 函数进行映射，而是只要能够映射为 “指数族分布” 即可。定义 $h(s,a;\theta)$ 函数为 “动作偏好值”，将离散型的策略 $\pi(a \vert s;\theta)$ 视为关于 $\theta$ 的一个函数，有

    \[\pi(a \vert s;\theta) \rightarrow \frac{e^{h(s,a;\theta)}}{\sum_{a'}e^{h(s,a';\theta)}}\]

  • 如果动作 $a$ 是连续随机变量，服从的分布可以有很多种，不妨认为服从 高斯分布

    这里将高斯分布中的 $\mu,\sigma$ 看作参数 $\theta$ 的函数，若 $\theta$ 能够求解， $\mu,\sigma$ 同样也可以被求解，最终求解整个分布

    \[\mu=\mu(s;\theta),\sigma=\sigma(s;\theta)\]

    若 $a$ 是服从 1 维随机变量的高斯分布，策略函数 $\pi(a \vert s;\theta)$ 表示如下

    \[\pi(a \vert s;\theta) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(a-\mu)^2}{2\sigma^2}}\]

为了改进策略函数，需要围绕参数 $\theta$ 构建一个目标函数 $J(\theta)$，然后通过梯度下降（上升）的方式更新参数。

在后面我们会发现，最终需要计算目标函数的梯度，相当于计算策略函数的对数的梯度，但通常我们不会直接使用策略函数的对数的梯度，因为可以采用成熟的深度学习框架（PyTorch或者TensorFlow）自动求导来完成。

2.3. 策略梯度

确定策略函数后，下一步就是建立策略梯度的概念。我们首先从价值函数的梯度出发，引出策略梯度的定义。

2.3.1. 回顾价值梯度

首先回顾 Q-Learning 的核心思想，通过一步采样更新 Q 值

\[q(s_t,a_t)\leftarrow q(s_t,a_t)+\alpha[r_{t+1}+\gamma\max_a q(s_{t+1},a)−q(s_t,a_t)]\]

上述更新过程可以收敛，意味着 TD-Error 最终收敛至零

\[r_{t+1}+\gamma\max_a q(s_{t+1},a)−q(s_t,a_t) \rightarrow 0\]

那么我们可以构造一个参数为 $\theta$ 的深度神经网络，用来估计价值函数，即 DQN 方法

\[q(s,a) = q(s,a; \theta)\]

则训练用的损失函数可设计为

\[L(\theta) = \mathbb{E} \{[r_{t+1}+\gamma\max_a q(s_{t+1},a; \theta)−q(s_t,a_t; \theta)]^2\}\]

然后，通过梯度下降更新神经网络的参数，使得损失函数 $L(\theta)$ 最小。 \(\theta \leftarrow \theta - \alpha \nabla_{\theta} L(\theta)\)

其中，$\alpha$ 是学习率。采用分离拷贝思路后，损失函数的梯度可以写为

\[\nabla_{\theta} L(\theta) = \alpha[r_{t+1}+\gamma\max_a q(s_{t+1},a; \theta)−q(s_t,a_t; \theta)]\nabla_{\theta} q(s_t,a_t; \theta)\]

可以看出，我们从 Q-Learning 的 TD Error 出发定义出损失函数，对损失函数求梯度可得价值梯度。通过梯度下降找到最优参数 $\theta$，进而得到最优价值函数。

实际上，价值梯度并没有严格的定义，因为我们并不关心其具体形式，上述损失函数已经可以保证我们找到最优网络参数。可以粗略的认为，狭义的价值梯度是 $\nabla_{\theta} q(s_t,a_t; \theta)$，而广义的价值梯度即为损失函数的梯度。

2.3.2. 策略梯度

类似地，我们需要定义一个策略梯度来更新神经网络的参数，最终使得策略达到最优。神经网络的输出是前面定义的策略函数 $\pi(a \vert s;\theta)$，那么损失函数的表达式中必然要「显式包含」策略函数，这样才能衡量输出和真值之间的误差，即

\[J(\theta) = J(\pi(a\vert s;\theta))\]

如果能给出上述损失函数的表达式，更进一步如果能直接给出损失函数梯度的表达式，就可以直接进行梯度下降（上升？）更新网络参数

\[\theta \leftarrow \theta + \alpha \nabla_\theta J(\pi(a\vert s ; \theta))\]

若我们定义 策略梯度 为上述损失函数的梯度，那么问题就转化为：

  • 损失函数 $J(\pi(a\vert s;\theta))$ 的具体形式是什么？
  • 损失函数的梯度（即策略梯度）$\nabla_\theta J(\pi(a\vert s;\theta))$ 的具体形式是什么？
  • 如何计算损失函数的梯度（即策略梯度）？梯度下降还是梯度上升？

3. 策略梯度的计算

3.1. 基于累计奖励的策略梯度

回想强化学习的目标是使得获得的奖励最大化，因此计算策略梯度的目的，也是为了更新神经网络的参数，使神经网络产生的能够得到大的奖励的动作的概率变大，即得到更优的策略使得获得的奖励最大化。

神经网络的输出为策略函数 $\pi(a\vert s;\theta)$，其中 $\theta$ 是神经网络的参数。假设采样一条马尔科夫轨迹如下

\[\tau = {s_1,a_1,r_1,s_2,a_2,r_2,...,s_T,a_T,r_T}\]

那么该轨迹发生的概率为

\[p_{\theta}(\tau) = p(s_1)\prod_{t=1}^T \pi(a_t\vert s_t;\theta)p(s_{t+1}\vert s_t,a_t)\]

其中，$p(s_1)$ 为初始状态的概率；$p(s_{t+1}\vert s_t,a_t)$ 为环境转移概率。注意这两个概率均与网络参数无关。

不考虑折扣衰减，该轨迹获得的累计奖励为

\[R(\tau) = \sum_{t=0}^T r_t\]

因此我们可以定义目标函数为

\[\textcolor{blue}{J(\theta) = \mathbb{E} [R(\tau)] = \mathbb{E}\left[\sum_{t=1}^T r_t\right]}\]

由于马尔科夫链是采样得到的，因此当前策略可获得的期望奖励为

\[\mathbb{E} [R(\tau)] = \sum_{\tau} p_{\theta}(\tau)R(\tau)\]

定义策略梯度为

\[\nabla_{\theta}J(\theta) = \nabla_{\theta}\mathbb{E} [R(\tau)] = \nabla_{\theta}\sum_{\tau} p_{\theta}(\tau) R(\tau) = \sum_{\tau} \nabla_{\theta}p_{\theta}(\tau) R(\tau)\]

注意，强化学习的目的是最大化这个期望奖励，因此需要用梯度上升来更新神经网络参数。

\[\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)\]
  • 问题转化为：如何计算 $\nabla_{\theta}p_{\theta}(\tau)$

注意到 $p_{\theta}(\tau)$ 是许多概率连乘的形式，如果直接计算其梯度，势必存在数据下溢（概率都是小于等于 1 的，多个概率连乘后数值会非常小），需要想办法避免。一种直觉思路是通过取 对数 把连乘转化为连加。

对 $\ln f(x)$ 函数求梯度具备如下性质

\[\nabla_{x} \ln f(x) = \frac{\nabla_{x} f(x)}{f(x)}\]

因此有

\[\nabla_{x} f(x) = f(x)\nabla_{x} \ln f(x)\]

将 $p_{\theta}(\tau)$ 带入即可得

\[\nabla_{\theta}p_{\theta}(\tau) = p_{\theta}(\tau)\nabla_{\theta} \ln p_{\theta}(\tau)\]

因此有

\[\begin{aligned} \nabla_{\theta}J(\theta) &= \sum_{\tau} \nabla_{\theta}p_{\theta}(\tau) R(\tau)\\ &= \sum_{\tau} p_{\theta}(\tau)\nabla_{\theta} \ln p_{\theta}(\tau) R(\tau) \\ &=\mathbb{E}_{\tau\sim p_{\theta(\tau)}}[\nabla_{\theta} \ln p_{\theta}(\tau) R(\tau)] \end{aligned}\]
  • 问题转化为：如何计算 $\nabla_{\theta} \ln p_{\theta}(\tau)$

首先通过蒙特卡洛方法进行 $N$ 次采样来近似估计期望

\[\begin{aligned} \nabla_{\theta}J(\theta) &=\mathbb{E}_{\tau\sim p_{\theta(\tau)}}[\nabla_{\theta} \ln p_{\theta}(\tau) R(\tau)]\\ &=\frac{1}{N} \sum_{n=1}^N \nabla_{\theta} \ln p_{\theta}(\tau_n) R(\tau_n) \end{aligned}\]

其中，$\tau_n$ 是第 $n$ 次采样得到的轨迹。那么对于这条具体的轨迹有

\[\begin{aligned} \nabla_{\theta} \ln p_{\theta}(\tau_n) &= \nabla_{\theta} \left[\ln p(s_1) + \sum_{t=1}^T \ln \pi_{\theta}(a_t\vert s_t) +\sum_{t=1}^T \ln p(s_{t+1}\vert s_t,a_t)\right]_n\\ &= \nabla_{\theta}\sum_{t=1}^T\ln \pi_{\theta}(a_t^n\vert s_t^n) = \sum_{t=1}^T\nabla_{\theta}\ln \pi_{\theta}(a_t^n\vert s_t^n)\\ \end{aligned}\]

上式可以看出，利用对数函数把连乘转为连加的好处在于。中第一项和第三项与网络参数 $\theta$ 无关，因此对其求梯度为 0，仅剩第二项。

带回前式可得到如下更新式

\[\nabla_{\theta}J(\theta) = \frac{1}{N}\sum_{n=0}^N \sum_{t=1}^T \nabla_{\theta}\ln \pi_{\theta}(a_t^n\vert s_t^n) R(\tau_n)\]

最后，重新把策略梯度写为期望的形式，有

\[\textcolor{red}{\nabla_{\theta}J(\theta)=\mathbb{E} [\nabla_{\theta}\ln \pi_{\theta}(A\vert S) R]}\]

上述策略梯度存在一个局限，即只适用于蒙特卡洛采样能够采样到终止状态的情况，此时累计奖励可以计算得到特定的值。如果采样无法达到终止状态，轨迹就无限延申，就无法计算累计奖励了。

3.2. 基于初始状态价值的策略梯度

为了解决基于累计奖励的策略梯度在蒙特卡洛采样无限时无法求解问题，引入折扣因子，对应的目标函数为

\[\textcolor{blue}{J(\theta) = \mathbb{E} [R(\tau)]= \mathbb{E}[\sum_{t=1}^T \gamma^{t-1} r_t]}\]

注意到，上式右侧的求和就是回报的定义式（累计奖励的折扣和），带上期望就是价值函数的定义式，相当于利用初始状态的状态价值函数来衡量轨迹的优劣，因此有

\[J(\theta) = V_{\pi}(s)\]

那么有

\[\nabla_{\theta}J(\theta) = \nabla_{\theta}V_{\pi}(s)\]

上述策略梯度没有显式包含策略函数 $\pi_{\theta}(a\vert s)$，需要通过策略梯度定理将其进一步展开。

3.3. 策略梯度定理

首先使用贝尔曼期望方程对 $V_{\pi}(s)$ 进行展开

\[\nabla_{\theta}V_{\pi}(s) = \nabla_{\theta}\sum_{a\in \mathcal{A(s)}} \pi(a\vert s)q_{\pi}(s,a) = \sum_{a\in \mathcal{A(s)}}\nabla_{\theta}[\pi(a\vert s)q_{\pi}(s,a)]\]

注意到求梯度是对网络参数 $\theta$ 进行的，而所有和策略 $\pi$ 有关的项均隐含 $\theta$，所以上述式子需要采用乘法求导的形式展开

\[\begin{aligned} \nabla_{\theta}V_{\pi}(s) &= \sum_{a\in \mathcal{A(s)}}\nabla_{\theta} [\pi(a\vert s)q_{\pi}(s,a)]\\ &= \sum_{a\in \mathcal{A(s)}} [\nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a) + \pi(a\vert s) \nabla_{\theta}q_{\pi}(s,a)]\\ \end{aligned}\]

其中第二项

\[\begin{aligned} \nabla q_{\pi} (s,a) &= \nabla \sum_{s^\prime,r} P(s^\prime,r\vert s,a)[r+\gamma V_{\pi}(s^\prime)]\\ &=\nabla \sum_{s^\prime,r}^{s^\prime,r} P(s^\prime,r|s,a) r + \nabla \sum_{s^\prime,r} \gamma P(s^\prime,r|s,a)V_{\pi}(s^\prime)\\ &=\nabla \sum_{s^\prime,r} \gamma P(s^\prime,r|s,a)V_{\pi}(s^\prime)\\ &=\gamma \sum_r P(r\vert s,a)\sum_{s^\prime} P(s^\prime\vert s,a) \nabla V_{\pi}(s^\prime)\\ &=\gamma \sum_{s^\prime} P(s^\prime\vert s,a) \nabla V_{\pi}(s^\prime) \end{aligned}\]

带回梯度式子，即

\[\nabla_{\theta}V_{\pi}(s) = \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a) + \sum_{a\in \mathcal{A(s)}} \pi(a\vert s)\gamma \sum_{s^\prime} P(s^\prime\vert s,a) \nabla_{\theta} V_{\pi}(s^\prime)\]

可以看出，上式呈现出 $\nabla_{\theta}V_{\pi}(s)$ 的迭代形式。为了更进一步确定迭代关系，再次对 $\nabla_{\theta}V_{\pi}(s^\prime)$ 展开，有

\[\nabla_{\theta}V_{\pi}(s^\prime) = \sum_{a^\prime\in \mathcal{A(s^\prime)}} \nabla_{\theta}\pi(a^\prime\vert s^\prime) q_{\pi}(s^\prime,a^\prime) + \sum_{a^\prime\in \mathcal{A(s^\prime)}} \pi(a^\prime\vert s^\prime)\gamma \sum_{s^{\prime\prime}} P(s^{\prime\prime}\vert s^\prime,a^\prime) \nabla_{\theta} V_{\pi}(s^{\prime\prime})\]

带回梯度式子并且完全展开，有

  • 第一项
\[\sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a)\]

  • 第二项

    \[\begin{aligned} &\sum_{a\in \mathcal{A(s)}} \pi(a\vert s)\gamma \sum_{s^\prime} P(s^\prime\vert s,a)\cdot \sum_{a^\prime\in \mathcal{A(s^\prime)}} \nabla_{\theta}\pi(a^\prime\vert s^\prime) q_{\pi}(s^\prime,a^\prime) \\ =&\gamma \sum_{s^\prime}\sum_{a\in \mathcal{A(s)}} \pi(a\vert s) P(s^\prime\vert s,a)\cdot \sum_{a^\prime\in \mathcal{A(s^\prime)}} \nabla_{\theta}\pi(a^\prime\vert s^\prime) q_{\pi}(s^\prime,a^\prime) \\ =&\gamma \sum_{s^\prime} \mathcal{P}(s^\prime\vert s)\cdot \sum_{a^\prime\in \mathcal{A(s^\prime)}} \nabla_{\theta}\pi(a^\prime\vert s^\prime) q_{\pi}(s^\prime,a^\prime)\\ \end{aligned}\]

    上式仅包含前后状态的变量 $s,s^\prime$ 和转移次数常量 $k=1$（$a$ 最终会被求和吸收积分掉），因此可进一步写为通项式：

    \[\gamma \sum_{x\in S} \mathcal{P}(s\rightarrow x, k, \pi)\cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert x) q_{\pi}(x,a)\]

    同时，注意到第一项也符合上述通项式（$k=0,\gamma = 1$）

  • 第三项

    \(\sum_{a\in \mathcal{A(s)}} \pi(a\vert s)\gamma \sum_{s^\prime} P(s^\prime\vert s,a) \cdot \sum_{a^\prime\in \mathcal{A(s^\prime)}} \pi(a^\prime\vert s^\prime)\gamma \sum_{s^{\prime\prime}} P(s^{\prime\prime}\vert s^\prime,a^\prime) \nabla_{\theta} V_{\pi}(s^{\prime\prime})\) 注意到第三项仍然是个迭代式，可以继续展开，且展开除了最后一项，前面均符合前述通项式。

至此， $\nabla_{\theta} V_\pi(s)$ 的迭代式表示如下

\[\nabla_{\theta}V_{\pi}(s) = \sum_{s\in S} \sum_{k=0}^{\infty} \gamma^{k} \mathcal{P}(s\rightarrow x, k, \pi)\cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert x) q_{\pi}(x,a)\]

将公式中所有 $s$ 替换为初始状态 $s_0$，将所有 $x$ 替换为 $s$，可得

\[\nabla_{\theta}V_{\pi}(s_0) = \sum_{s\in S} \sum_{k=0}^{\infty} \gamma^{k} \mathcal{P}(s_0\rightarrow s, k, \pi)\cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a)\]

其中，

  • $\mathcal{P}(s_0\rightarrow s, k, \pi)$ 表示初始状态 $s_0$ 经过 $k$ 次状态转移最终到达 $s$ 的概率；
  • $\sum_{k=0}^{\infty} \mathcal{P}(s_0\rightarrow s, k, \pi)$ 表示在整条轨迹序列中，状态 $s$ 出现的平均次数，将其记为 $\eta(s)$；
  • 那么状态 $s$ 出现的概率 $\mu(s)$ 可定义为其出现的平均次数除以所有状态出现的平均次数的和，即 $\mu(s) = {\eta(s)}/{\sum_{s^\prime} \eta(s^\prime)}$

则

\[\begin{aligned} \nabla_{\theta}V_{\pi}(s_0) &= \sum_{s\in S} \gamma^{k} \eta(s) \cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a)\\ &= \sum_{s\in S} \gamma^{k} \mu(s)\sum_{s^\prime\in S} \eta(s^\prime) \cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a)\\ &= \sum_{s^\prime\in S}\left(\sum_{s\in S} \eta(s^\prime) \gamma^{k} \mu(s) \right) \cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a)\\ \end{aligned}\]

我们希望把前面对状态 $s$ 的求和重新表示为某种期望的形式

\[\nabla_{\theta}J(\theta) =\mathbb{E}_{?}\left[ \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a) \right]\]

问题转化为，确定期望符号中的概率分布是什么（也即上式中的 ? 部分）。既然是分布，不妨假设其概率分布为 $\rho_\pi(s)$，该分布不仅和策略函数 $\pi(a\vert s;\theta)$ 相关，还与环境（状态转移概率）相关，那么策略梯度变为

\[\begin{aligned} \nabla_{\theta}V_{\pi}(s_0) &\doteq \sum_{s^\prime\in S}\rho_{\pi}(s^\prime) \cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a)\\ &= \sum_{s\in S}\rho_{\pi}(s) \cdot \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a) \end{aligned}\]

则

\[\nabla_{\theta}J(\theta) = \mathbb{E}_{s\sim \rho_{\pi}(s)}\left[ \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s) q_{\pi}(s,a) \right]\]

继续观察，上式还存在一个求和符号，因此存在一个想法是将该部分也化为期望的形式。但该求和符号的消除需要借助策略函数，因此需要对 $\nabla_{\theta}\pi(a\vert s;\theta)$ 进行变换，借助之前 $\ln f(x)$ 函数梯度的性质，有

\[\begin{aligned} \nabla_{\theta}J(\theta) = & \mathbb{E}_{s\sim \rho_{\pi}(s)}\left[ \sum_{a\in \mathcal{A(s)}} \nabla_{\theta}\pi(a\vert s;\theta) q_{\pi}(s,a) \right]\\ = & \mathbb{E}_{s\sim \rho_{\pi}(s)}\left[ \sum_{a\in \mathcal{A(s)}} \pi(a\vert s;\theta)\nabla_{\theta}\ln\pi(a\vert s;\theta) q_{\pi}(s,a) \right]\\ = & \mathbb{E}_{s\sim \rho_{\pi}(s), a\sim \pi} \left[ \nabla_{\theta}\ln\pi(a\vert s;\theta) q_{\pi}(s,a) \right]\\ \end{aligned}\]

将期望的下标进行简化，最终我们得到了一般形式的基于初始状态价值的策略梯度

\[\textcolor{red}{\nabla_{\theta}J(\theta) = \mathbb{E} \left[ \nabla_{\theta}\ln\pi(A\vert S;\theta) q_{\pi}(S,A) \right]}\]

上式中的 “=” 并非严格意义的相等，而是包含 ”相等、约等于、正比于“ 三种形式，具体形式与折扣因子取值、初始状态分布有关。

有关策略改进定理还可参考：https://zhuanlan.zhihu.com/p/491647161

注意，同样需要用梯度上升来更新神经网络参数

\[\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)\]

4. 基于策略梯度的参数更新

梯度上升算法中，将待更新参数的下标加上，得到如下更加严谨的形式

\[\begin{aligned} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta_t} J(\theta)\\ &= \theta_t + \alpha \mathbb{E} \left[ \nabla_{\theta_t}\ln\pi(A\vert S;\theta_t) q_{\pi}(S,A) \right]\\ \end{aligned}\]

期望符号可以通过「随机梯度下降」的方式来消除

\[\theta_{t+1} = \theta_t + \alpha \nabla_{\theta_t}\ln\pi(a\vert s;\theta_t) q_{\pi}(s,a)\]

期望符号包含了对 $S,A$ 的采样，其中

  • $S \sim d $ 或 $S \sim \rho$ 是策略 $\pi$ 下的长期分布，但实际上我们有样本就不错了，所以实际应用中不考虑；
  • $A \sim \pi(A\vert S;\theta)$ 需要实际采样才能得到，因此策略梯度法是个 on-policy 方法。

虽然消除了期望符号，但其中涉及的 $q_{\pi}(s, a)$ 仍然未知，有两种近似求解的思路：

  • MC：使用 Monte-Carlo 采样得到真实回报 $G_t$ 来近似估计，称其为 REINFORCE；
  • TD：使用时序差分算法，对应 Actor-Critic 等一系列方法。

4.1. REINFORCE

根据 Q 函数的定义有

\[q_{\pi_{\theta}}(s_t, a_t) = \mathbb{E} [G_t\vert s_t, a_t]\]

带入策略梯度定理有

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) G_t \right]\]

至此，我们可以通过采样 $\nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) G_t$ 神经网络参数 $\theta$ 进行更新。这就是 REINFORECE。REINFORCE 的本质就是用 $G_t$ 代替 $q_{\pi}(s_t, a_t)$。

用于估计最优策略的REINFORCE算法表示如下（采用增量更新的方式）

  • 输入：可微策略函数 $\pi(a \vert s;\theta)$，衰减因子 $\gamma$，学习率 $\alpha$
  • 初始化：策略函数的参数 $\theta$
  • 训练过程：
    • repeat 根据 $\pi_{\theta}$ 采样一条轨迹：$s_0, a_0, r_1, s_2, a_2, r_3, \cdots$
    • loop $t=T-1, T-2, \cdots, 1,0$
      • $\quad G\leftarrow \gamma G + r_{t+1}$
      • $\quad \theta \leftarrow \theta + \alpha \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) G $

根据定义，因为 $G_t$ 是 $Q(s,a)$ 的无偏估计，所以基于蒙特卡洛采样的方式进行参数更新的 REINFORCE 算法，得到的结果就是策略梯度的无偏估计，那么其方差呢？

结论：基于蒙特卡洛采样的方式进行参数更新的 REINFORCE 算法方差很大。通过观察策略梯度式

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) G_t \right]\]

我们可以看出，$\nabla_{\theta}\ln\pi(a_t\vert s_t;\theta)$ 相当于 $G$ 的一个系数或者说权重，对于方差而言只起到放缩作用（根据公式 $Var(aX) = a^2Var(X)$），实际方差还是取决于 $G$ 本身。而 $G$ 的方差

\[Var(G_t) = Var(R_{t+1}) + Var(R_{t+2}) + \cdots\]

由此可以看出，方差大来源于两个原因：

  • 若不同 $s$ 对应的 $R$ 范围相差较大，再加上 MC 的随机性，那么每一步的 $R$ 都会有较大的方差;
  • 因为采样轨迹长度的原因，出现方差累积。

相应的解决方法如下：

  • 通过添加基线缓解;
  • 使用 TD 方法代替 MC 方法，即通过Actor-Critic方法解决。

4.2. REINFORCE with baseline

通过添加基线（baseline）可以减小方差。具体形式如下

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) G_t \right]\]

添加基线 $b(s)$ 后，目标函数的梯度变为

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) (G_t-b(s_t)) \right]\]

参数更新方式变为

\[\theta \leftarrow \theta + \alpha (G_t - b(s_t)) \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta)\]

基线 $b(s)$ 可为不与动作 $a$ 有关的任意变量或者函数，因为它并不会改变策略梯度的期望，证明如下

\[\begin{aligned} \nabla_{\theta}J(\theta) &\propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) (G_t-b(s_t)) \right]\\ &\propto \sum_{a}\pi(a\vert s) \nabla_{\theta}\ln \pi(a\vert s;\theta)(G_t-b(s_t))\\ &\propto \sum_{a} \nabla_{\theta}\pi(a\vert s;\theta)(G_t-b(s_t)) \end{aligned}\]

因为 $b(s)$ 与动作 $a$ 无关，可以提到求和符号外面，但注意 $G_t$ 不可以提到求和符号外面

\[\begin{aligned} \nabla_{\theta}J(\theta) &\propto \sum_{a} \nabla_{\theta}\pi(a\vert s;\theta)(G_t-b(s_t))\\ &\propto \sum_{a} G_t \nabla_{\theta}\pi(a\vert s;\theta) - b(s_t) \sum_{a} \nabla_{\theta}\pi(a\vert s;\theta)\\ \end{aligned}\]

对于后一项，交换梯度符号和求和符号，有

\[b(s_t) \sum_{a} \nabla_{\theta}\pi(a\vert s;\theta) =b(s_t)\nabla_{\theta} \sum_{a} \pi(a\vert s;\theta) = b(s_t)\nabla_{\theta} 1 = 0\]

得证。

关于基线的更多内容参考：https://zhuanlan.zhihu.com/p/636907461

为什么引入基线可以减小方差？证明如下：

首先根据方差的定义

\[Var(X) = E(X^2)-E(X)^2\]

那么有

\[Var(\nabla_{\theta}J(\theta)) = Var(\nabla_{\theta}^2)-\nabla_{\theta}^2 E(\nabla_{\theta})\]

我们又知道引入基线不改变期望，因此方差的第二项取值与是否包含基线无关，则只需要关注第一项即可

\[\begin{aligned} Var \nabla_{\theta}J(\theta)^2 &= E[\nabla_{\theta}\ln\pi_{\theta}(a_t\vert s_t)^2\cdot (G_t - b(s_t))^2] \\ &= E[\nabla_{\theta}\ln\pi_{\theta}(a_t\vert s_t)^2]\cdot E[(G_t - b(s_t))^2] \end{aligned}\]

思考：什么基线能使上式取到最小值？$\to$ 这是一个求极值问题 $\to$ 上式对基线求偏导并另其为零。

\[\begin{aligned} &\frac{\partial}{\partial b(s_t)}Var\nabla_{\theta}J( \theta )^2=\mathbb{E}\{2\left( G_t-b( s_t ) \right) [ \nabla _{\theta}\ln \pi _{\theta}( a_t|s_t ) ^2 ] \}=0\\ \Rightarrow & \mathbb{E}\{G_t [ \nabla _{\theta}\ln \pi _{\theta}( a_t|s_t ) ^2 ] \}=\mathbb{E}\{b( s_t ) [ \nabla _{\theta}\ln \pi _{\theta}( a_t|s_t ) ^2 ] \} \end{aligned}\]

则

\[b(s_t) = \frac{\mathbb{E}\{G_t [ \nabla _{\theta}\ln \pi _{\theta}( a_t|s_t ) ^2 ] \}}{\mathbb{E}[ \nabla _{\theta}\ln \pi _{\theta}( a_t|s_t ) ^2 ]}\]

当基线是关于 $G_t$ 期望的上述估计时，方差最小。上述估计是一个对 $G_t$ 的带权重估计值，但其中权重的求解需要用到梯度信息，这是未知的。因此实际情况中我们也不会用这个理论最优的基线。

实际情况中，我们直接忽略权重，将基线设置为次优的情况

\[\begin{aligned} &b(s) = \mathbb{E}[G_t] = \mathbb{E}(G_t \vert s=s_t) = v_\pi(s)\\ \text{or}\quad &b(s) = \mathbb{E}[G_t] = \mathbb{E}(G_t \vert s=s_t,a=a_t) = q_{\pi}(s,a) \end{aligned}\]
  • 对于第一种次优情况，相当于将基线设为「状态价值函数」；
  • 对于第二种次优情况，相当于将基线设为「状态-动作价值函数」。

当基线函数选为 状态价值函数时，更进一步，因为 REINFORCE 本身是基于蒙特卡洛方法，那么自然而然可以同样使用蒙特卡洛方法来学习该状态价值函数，即

\[b(s) = {v}(s_t;{w})\]

其中 $w$ 是另一套习得的参数。此时，策略梯度的表达式变为

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\underbrace{\pi(a_t\vert s_t;\theta)}_{\text{actor}} (G_t-\underbrace{v(s_t;w)}_{\text{critic}}) \right]\]

到此为止，我们就可以将 REINFORCE 算法转化为 Actor-Critic 算法，其中参数 $\theta$ 对应策略梯度部分的神经网络，扮演 Actor 的角色；而 $w$ 对应价值估计部分的神经网络，扮演 Critic 的角色。

更进一步，类似于基于价值的强化学习方法中，MC 到 TD 方法的逻辑演变，这里我们同样不需要采样完整的一条轨迹，而是仅采样一步，后续通过自举的方式逐步估计完整的轨迹，对应策略梯度表达式变为

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\underbrace{\pi(a_t\vert s_t;\theta)}_{\text{actor}} (R_{t+1}+\gamma \underbrace{v(s_{t+1};w)-v(s_t;w)}_{\text{critic}}) \right]\]

此时价值网络的更新形式为

\[\begin{aligned} \delta_t &= R_{t+1}+\gamma v(s_{t+1};\omega)-v(s_t;\omega)\\ J(\omega) &= \frac{1}{2} \delta_t^2\\ \omega &\leftarrow \omega - \alpha_{\omega} \delta_t \nabla_{\omega}v(s;\omega) \end{aligned}\]

此时策略网络的更新形式为

\[\begin{aligned} \delta_t &= R_{t+1} + \gamma {v}(s_{t+1};w)-{v}(s_t;{w})\\ \nabla_{\theta}J(\theta) &\propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) \delta_t \right]\\ \theta &\leftarrow \theta + \alpha \delta_t \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) \end{aligned}\]

算法的训练的伪代码如下，该算法又被简称为 「V Actor-Critic（VAC）算法」

  • 输入：
    • 可微策略函数 $\pi(a \vert s;\theta)$
    • 可微的价值函数 ${v}(s;w)$
    • 衰减因子 $\gamma$，学习率 $\alpha_\theta,\alpha_w$
  • 初始化：
    • 策略函数的参数 $\theta$
    • 价值函数的参数 $w$
  • 训练过程：
    • loop 状态 $s$ 没有结束时
      • 根据策略采样：$a\sim \pi(\cdot, s;\theta)$
      • 执行动作 $a$， 得到奖励 $R$，转移状态到 $s^\prime$
      • $\delta \leftarrow R + \gamma {v}(s^\prime;w) - {v}(s;w)$
      • $w \leftarrow w + \alpha_w \delta\nabla_{w}{v}(s;w)$
      • $\beta \leftarrow \gamma \delta$
      • $\theta \leftarrow \theta + \alpha \beta \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta)$

若采用状态-动作价值函数 $q(s,a)$ 作为基线函数，并使用神经网络对其进行估计，有

\[b(s_t) = q(s_t, a_t;\omega)\]

此时策略梯度表达式为

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\underbrace{\pi(a_t\vert s_t;\theta)}_{\text{actor}} (R_{t+1}+\gamma \underbrace{q(s_{t+1},a_{t+1};w)-q(s_t,a_t;w)}_{\text{critic}}) \right]\]

此时价值网络的更新形式为

\[\begin{aligned} \delta_t &= R_{t+1}+\gamma q(s_{t+1}, a_{t+1};\omega)-q(s_t, a_t;\omega)\\ J(\omega) &= \frac{1}{2} \delta_t^2\\ \omega &\leftarrow \omega - \alpha_{\omega} \delta_t \nabla_{\omega}q(s,a;\omega) \end{aligned}\]

注意到，这里实际上就是采用 SARSA 值函数近似 来进行价值网络更新。

对于策略网络的目标函数的梯度，应该使用原始的策略梯度形式，此时策略网络的更新形式为

\[\begin{aligned} \nabla_{\theta}J(\theta) &\propto \mathbb{E} [ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) q(s_t,a_t;\omega)]\\ \theta &\leftarrow \theta + \alpha_{\theta}{q(s,a;\omega)}\nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) \end{aligned}\]

该算法又被简称为 「Q Actor-Critic（QAC）算法」。

4.5. Advantage Actor-Critic (A2C)

前面介绍 REINFORCE 的时候，我们通过引入基线降低方差，并且表明将基线函数设为价值函数是一个较优的选择。

本着这种思想，我们再次回顾策略梯度的原始目标函数梯度式，然后对其引入状态价值函数 $v_{\pi}(s_t)$ 作为基线，有

\[\nabla_{\theta}J(\theta) \propto \mathbb{E} \left[ \nabla_{\theta}\ln\pi(a_t\vert s_t;\theta) (q_{\pi}(s_t,a_t)-v_{\pi}(s_t)) \right]\]

我们称 $\textcolor{red}{\delta_t(s_t,a_t) = q_{\pi}(s_t,a_t)-v_{\pi}(s_t)}$ 为 优势函数。优势函数表示在状态 $s$ 下采取动作 $a$ 相对于平均水平的优势。

  • 如果优势函数大于零，则说明该动作比平均动作好
  • 如果优势函数小于零，则说明当前动作还不如平均动作好。

因此原先用 Critic 网络对 $q$ 函数的估计就可以改成对优势函数的估计，估算每个 $q(s_t,a_t)$ 对相对于平均值 $V(s_t)$ 的优势。这种算法就是 Advantage Actor Critic ，即 A2C。

4.5.1. 探索与利用

根据 $\ln f(x)$ 梯度性质

\[\nabla_\theta \ln\pi(a\vert s;\theta) = \frac{\nabla_\theta \pi(a\vert s;\theta)}{\pi(a\vert s;\theta)}\]

则 A2C 的梯度上升式可改写为

\[\begin{aligned} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta_t} \ln\pi(a_t\vert s_t;\theta_t)\delta_t(a_t,s_t)\\ &= \theta_t + \alpha \left(\frac{\delta_t(a_t,s_t)}{\pi(a_t\vert s_t;\theta_t)}\right) \nabla_\theta \pi(a_t\vert s_t;\theta_t)\\ &= \theta_t + \alpha \textcolor{red}{\beta_t} \nabla_\theta \pi(a_t\vert s_t;\theta_t) \end{aligned}\]

这个式子其实在优化 $\pi(a_t\vert s_t;\theta_t)$。因为根据微分的性质，当 $\theta_{t+1}-\theta_t$ 足够小时，下面的式子成立

\[\pi(a_t\vert s_t;\theta_{t+1}) \approx \pi(a_t \vert s_t;\theta_t)+(\nabla_\theta \pi(a_t\vert s_t;\theta_t))^\top (\theta_{t+1}-\theta_t)\]

把前面的梯度上升式带进去，得

\[\begin{aligned} \pi(a_t\vert s_t;\theta_{t+1}) &\approx \pi(a_t \vert s_t;\theta_t)+(\nabla_\theta \pi(a_t\vert s_t;\theta_t))^\top (\theta_{t+1}-\theta_t)\\ &=\pi(a_t \vert s_t;\theta_t)+(\nabla_\theta \pi(a_t\vert s_t;\theta_t))^\top \alpha \beta_t \nabla_\theta \pi(a_t\vert s_t;\theta_t)\\ &=\pi(a_t \vert s_t;\theta_t)+ \alpha \beta_t \Vert \nabla_\theta \pi a_t\vert s_t;\theta_t\Vert^2 \end{aligned}\]

当 $\alpha_t\beta_t>0$ 但值比较小时，有

\[\pi(a_t\vert s_t;\theta_{t+1}) > \pi(a_t\vert s_t;\theta_t)\]

反之当 $\beta_t < 0$ 时，有

\[\pi(a_t\vert s_t;\theta_{t+1}) < \pi(a_t\vert s_t;\theta_t)\]

注意到，$\beta_t$ 和 $\textcolor{red}{\delta_t(a_t,s_t)}$ 成正比，和 $\pi(a_t\vert s_t;\theta_t)$ 成反比，因此

  • 当 $\delta_t(a_t,s_t)$ 较大时，$\beta_t$ 较大，新策略会更加倾向于选择该动作，即「利用」；
  • 当 $\pi(a_t\vert s_t;\theta_t)$ 较小时，$\beta_t$ 也较大，新策略会更加倾向于选择原本小概率被选择的动作，即「探索」；

所以 $\beta_t$ 可以巧妙地平衡探索和利用。并且其使用的是优势函数，其衡量了当前所选动作相对于平均基准的相对值，因此在探索和利用的平衡上更为合理。

4.5.2. 与 VAC 的关系

注意到，A2C 在具体实现的时候需要同时估计 $q(s_t, a_t)$ 和 $v(s_t)$，估计一个价值函数已经会存在误差了，估计两个价值函数误差会更大。但是我们知道 $q(s_t, a_t)$ 和 $v(s_t)$ 之间是存在关系的，在具体采样时，有

\[q(s_t, a_t) = r_{t+1} + \gamma v(s_{t+1})\]

此时我们发现，A2C 就是前面介绍过的 VAC 算法，价值网络只用估计 $v(s_t)$ 的值就够了。

4.6. 重要性采样

前面介绍的所有策略梯度方法都是 on-policy 方法，即实际进行动作采样的行为策略与待更新的目标策略相同，都是同一个神经网络。我们可以借鉴前面课程中（Q-Learning）介绍的方法，将其转为 off-policy 方法，这样可以更加充分利用已经采样得到的历史样本数据。

此处，我们引入重要性采样来实现上述转换。更加一般的情况下，重要性采样可以解决所有期望求解问题。

4.6.1. 重要性用于期望估计

假设样本 ${x_i}$ 是由其原始分布 $p_0$ 采样得到的，其期望和方差为

\[\mathbb{E}[x_i] = \mathbb{E}[X],\quad var[x_i] = var[X]\]

通过大数定律来近似期望，有

\[\begin{aligned} &\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\to \mathbb{E}[X],\quad \text{as } n\to \infty\\ & var(\bar{x}) = \frac{1}{n}var[X] \end{aligned}\]

假设样本 $x_i$ 是由根据另外一个分布 $p_1$ 采样得到的，问题变为：能否用 $x_i\sim p_i$ 来估计样本的原始分布？为什么要做上述事情？因为对于 off-policy 方法而言，样本采样来自分布行为策略 $\beta$（$p_1$），但是目标函数（使用策略梯度）中的期望是针对目标策略的，即 $\mathbb{E}_{A\sim \pi}[\star]$。

重要性采样的一般流程如下：

\[\mathbb{E}_{X\sim p_0}[X] = \int p_0(x)x\text{d}x = \int p_1(x)\underbrace{\frac{p_0(x)}{p_1(x)}x}_{f(x)}\text{d}x = \mathbb{E}_{X\sim p_1}[f(X)]\]

即可以通过右边的期望来估计原始分布下的期望。相比原始分布下的期望，新的期望更加好求

\[\begin{aligned} \mathbb{E}_{X\sim p_1}[\bar{f}(X)] &= \mathbb{E}_{X\sim p_1}[f(X)]=\frac{1}{n}\sum_{i=1}^n f(x_i),\quad \text{where } x\sim p_1\\ var_{X\sim p_1}[\bar{f}(X)] &= \frac{1}{n}var_{X\sim p_1}[f(X)] \end{aligned}\]

其中 $\textcolor{red}{p_0(x)/p_1(x)}$ 被称为「重要性权重」。

注意到，重要性权重中出现了 $p_0(x)$，这要求 $p_0$ 已知。那既然都已知了为什么不直接求期望呢？

因为就算样本原始分布是已知的，其期望求解也可能是十分困难的。比如：

  • 当 $p_0$ 的表达式十分复杂时，求积分（期望）难以计算；
  • 当 $p_0$ 是一个神经网络时，求积分（期望）求不出来；

对重要性采样总结如下

\[\begin{aligned} &{x_i}\sim p_1,\\ \bar{x} &= \frac{1}{n}\sum_{i=1}^n x_i\to \mathbb{E}_{X\sim p_1}[X]\\ \bar{f} &= \frac{1}{n}\sum_{i=1}^n \frac{p_0(x_i)}{p_1(x_i)}x_i\to \mathbb{E}_{X\sim p_0}[f(X)]\\ \end{aligned}\]

4.6.2. 重要性用于策略梯度

回顾基于初始状态价值的策略梯度式，策略梯度为

\[\nabla_{\theta}J(\theta) = \mathbb{E}_{s\sim \rho_{\pi}(s), \textcolor{blue}{a\sim \pi}} \left[ \nabla_{\theta}\ln\pi(a\vert s;\theta) q_{\pi}(s,a) \right]\]

引入重要性采样后，假设行为策略为 $\beta$ 用于产生样本，则策略梯度为

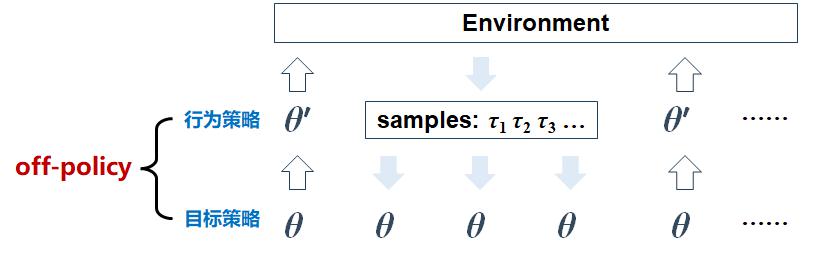
\[\nabla_\theta J(\theta) = \mathbb{E}_{S\sim \rho,\textcolor{red}{A\sim \beta}}\left[ \frac{\pi(A\vert S;\theta)}{\beta(A\vert s)} \nabla_\theta \pi(A\vert S;\theta) q_\pi(S,A) \right]\]

重要性采样保证了我们在将策略梯度方法变为 off-policy 后，策略梯度的期望估计依然保持不变。因此，我们可以不用和环境紧密绑定在一次，每次更新都要重新采样。前面我们也提过，有时候相比梯度上升计算，与环境进行采样交互反而耗时更长。通过重要性采样，我们完全可以使用行为策略（$\theta^\prime=\theta_{\text{frozen}}$）与环境进行大批次采样后，得到样本更新目标策略，经过若干次迭代再进行硬拷贝。如下图所示：

PPO

进一步，根据优势函数的定义，我们将重要性采样嵌入，则 A2C 的梯度上升式可改写为

\[\begin{aligned} \theta_{t+1} &= \theta_t + \alpha \textcolor{red}{\frac{\pi(a_t\vert s_t;\theta)}{\beta(a_t\vert s_t)}} \nabla_{\theta_t} \ln\pi(a_t\vert s_t;\theta_t)\delta_t(a_t,s_t)\\ &= \theta_t + \alpha \left(\frac{\delta_t(a_t,s_t)}{\beta(a_t\vert s_t)}\right) \nabla_\theta \pi(a_t\vert s_t;\theta_t) \end{aligned}\]

此时，对于 off-policy 方法，策略梯度方法中的行为策略 $\beta$ 不再发生变化，整个式子只剩下充分利用行为策略产生的样本（当 $\delta_t$ 比较大时增加对应的采样概率）。

相应的，价值网络的更新形式为

\[\begin{aligned} \delta_t &= R_{t+1}+\gamma v(s_{t+1};\omega_t)-v(s_t;\omega_t)\\ J(\omega) &= \frac{1}{2} \delta_t^2\\ \omega_{t+1} &= \omega_t - \alpha_{\omega} \textcolor{red}{\frac{\pi(a_t\vert s_t;\theta)}{\beta(a_t\vert s_t)}} \delta_t \nabla_{\omega}v(s_t;\omega_t) \end{aligned}\]

5. 确定性策略梯度（DPG）

前面介绍的所有策略梯度都是随机策略，即要求 $\pi(a\vert s;\theta) > 0,\; \forall(s,a)$，缺点在于其对动作 $a$ 的个数是有限的（回顾如下网络结构）

1
2
3
4

          +----+ ----> Q(s,a1)
  s  ---> |f(x)| ----> Q(s,a2)
          |  θ | ----> ...
          +----+ ----> Q(s,a3)

当然，我们也可以使用确定性策略，这样做的好处是可以适应连续无限的动作空间。

对于随机性策略和确定性策略两种情况，策略定义为 $\pi(a\vert s;\theta)\in[0,1]$，那么对于确定性策略，即给定一个状态输出一个确定的动作，其可定义为

\[a=\mu(s;\theta)\doteq \mu_\theta(s)\]

此时策略网络直接把状态映射到动作：$\mu:S\to A$，即

1
2
3
4

          +----+
  s  ---> |μ(x)| ----> a
          |  θ | 
          +----+

由于策略发生了变化，原来推导得到的策略梯度只适用于随机性策略，不再适用于确定性策略，需要重新推导。同样考虑基于初始状态价值的策略梯度，此时目标函数为

\[J(\theta) = V_{\mu}(s)\]

则相应的策略梯度为（推导略）

\[\nabla_\theta J(\theta) = \mathbb{E}_{S\sim \rho_\beta}[\nabla_\theta \mu(S)\left(\nabla_a q_\mu(S,a)\right)_{\vert a=\mu(S)}]\]

注意到其中并没有包含动作的分布 $A$，也就是说，确定性策略梯度是一个 off-policy 算法。并不要求我们必须按照哪个采样某个动作，因此可以使用任意行为策略 $\beta$ 进行采样。

DPG 的缺点很明显，对于每个状态，下一步的动作是确定的。这就导致只能做利用而不能做探索。这可能也是为什么要做 off-policy 的原因。我们可以设置行为策略为一个随机策略，采样后优化确定性的目标策略。

更进一步，行为策略往往被设置为 $\beta = \mu + N$ 的形式，其中 $N$ 为随机噪声。此时就可以避免周期性的硬拷贝，随着确定性目标策略 $\mu$ 得到优化，行为策略也随之得到优化。

当价值函数用线性函数近似时，即为 DPG 论文给出的原始方法。当使用深度神经网络时，该方法就变为 DDPG。

对于 DDPG 方法，其价值网络的更新部分不变

\[\omega_{t+1} = \omega_t - \alpha_{\omega} \delta_t \nabla_{\omega}q(s_t,a_t;\omega_t)\]

而策略网络的参数更新式为

\[\theta_{t+1} = \theta_t + \alpha_\theta \nabla_\theta \mu(s;\theta)\left( \nabla_a q(s_t, a; w_{t+1}) \right)_{\vert a=\mu(s_t)}\]

6. 参考文献

[1] 静静的喝酒. CSDN 策略梯度方法介绍——Value-Based强化学习方法 VS Policy-Based强化学习方法

[2] 静静的喝酒. CSDN 策略梯度方法介绍——策略梯度定理推导过程

[3] 静静的喝酒. 策略梯度方法介绍——蒙特卡洛策略梯度方法(REINFORCE)

[4] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction

Academic, Knowledge
reinforcement learning
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容

如何清理 .git 文件夹来减小 github 仓库大小

模式识别（线性分类器）