文章

精度损失和抖颤

发表于 更新于
作者 sirlis 9 分钟阅读

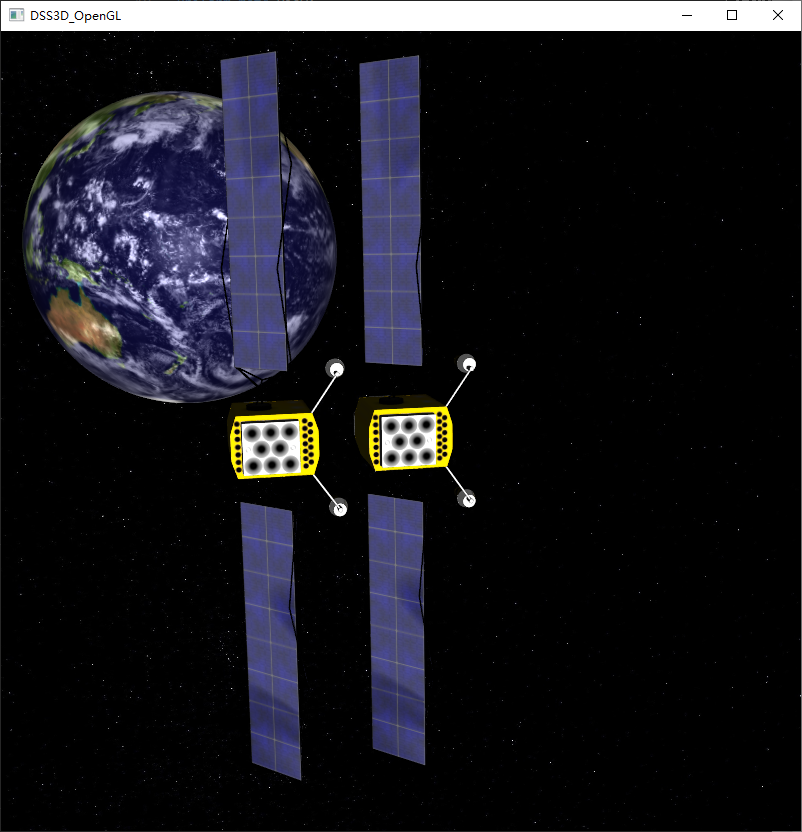
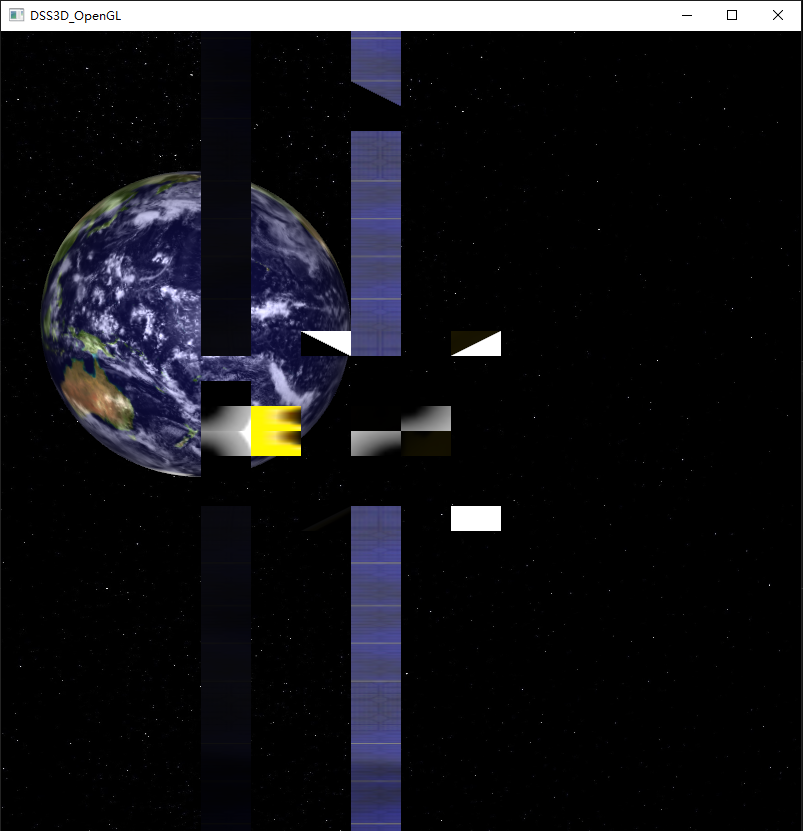
本文介绍了 OpenGL 中因渲染巨型尺度场景时出现的精度损失问题，以及随之而来的抖颤现象，深入分析了问题产生的原因，并最终给出了解决相对中心的渲染和相对视角的渲染解决方案。

1. 抖颤

使用OpenGL和Direct3D等图形api，图形处理单元（GPU）在内部采用单精度（32位）浮点数字进行操作，这些数字在很大程度上遵循IEEE 754规范。单精度值通常被认为有7个精确的十进制数字；因此，随着数字越来越大，数字的表示也越来越不精确。在大型场景渲染中，渲染远距离的对象很常见，如果渲染不正确，对象可能会在视觉上发生抖颤（jitter）。当观察者靠近物体时，这个问题变得更加明显。

alt text alt text

图 1 无抖颤和存在抖颤时的场景。场景按照真实比例渲染，单位米，两颗卫星运行于地球静止轨道（轨道半径42164137m），相距2.75m。

在航天领域的场景渲染中，精确地放置对象是最重要的。我们希望至少有1cm的精度。允许大约1cm增量的最大数字是131071（$2^{17}-1$）m。下面的代码片段显示了代码中正在分配的floatValue值，相应的注释则为该值实际存储在CPU系统内存中的值。可以看到，虽然存储的值不完全等于指定的值，但误差在0.5厘米内。

1
2
3
4
5
6
7
8
9
10
11

float floatValue;

floatValue = 131071.01; // 131071.0078125
floatValue = 131071.02; // 131071.0234375
floatValue = 131071.03; // 131071.0312500
floatValue = 131071.04; // 131071.0390625
floatValue = 131071.05; // 131071.0468750
floatValue = 131071.06; // 131071.0625000
floatValue = 131071.07; // 131071.0703125
floatValue = 131071.08; // 131071.0781250
floatValue = 131071.09; // 131071.0937500

当将floatValue再增加1cm时，其真实的指定值与实际存储的值之间的误差将超出1cm，其中一些不同的指定值对应着相同的存储值（代码中标*的位置）。

1
2
3
4
5
6
7
8
9
10
11

float floatValue;

floatValue = 131072.01; // 131072.0156250 *
floatValue = 131072.02; // 131072.0156250 *
floatValue = 131072.03; // 131072.0312500
floatValue = 131072.04; // 131072.0468750 **
floatValue = 131072.05; // 131072.0468750 **
floatValue = 131072.06; // 131072.0625000 *
floatValue = 131072.07; // 131072.0625000 *
floatValue = 131072.08; // 131072.0781250
floatValue = 131072.09; // 131072.0937500

在1:1的场景中，地球的半径可达6378137m，如果需要将一个物体放置在地球表面或者环绕地球的某个轨道上，其位置将远远大于131071m。物体的渲染精度将会变得很差，甚至难以达到分米级的精度。当观察者近距离观察这样一个对象时，该对象将发生抖颤。

如果可以从CPU将双精度（64位）浮点数字传递到GPU，并且GPU内部使用双精度浮点数字操作，那么在地球上或地球附近渲染的对象就不会出现抖动问题。但正如单精度值一样，物体离地球越远，精度就越差，抖动还是会发生。虽然没有进行精确计算，但是如果希望太阳系内的任何东西都能毫无问题地呈现出来，采用双精度浮点数很可能仍然难以胜任。

2. 相对于中心的渲染

90年代STK推出时，人们很快发现，当渲染地球和轨道上的物体（比如飞行器Space Shuttle时），抖动很快就表现出来了。一种解决方案是将对象相对于观察者进行渲染，而不是相对于世界坐标系原点进行渲染。世界空间中靠近观察者的像素区域要比远离观察者的区域小得多；因此，随着观察者接近对象，需要越来越精确地渲染对象且不能产生抖动。相对于观察者渲染对象可提供所需的精度。

首先介绍相对于中心的渲染（Rendering Relative to Center, RTC）技术。RTC技术的核心是重新计算ModelView矩阵，涉及的向量包括：

  • MV_GPU：从CPU传递到GPU的单精度的ModelView矩阵，用以将飞行器（SpaceShuttle）从世界空间变换至相机空间

  • MV_CPU：储存在CPU的双精度ModelView矩阵

  • SpaceShuttle_Eye：飞行器在相机空间中相对于观察者的坐标

  • SpaceShuttle_World：飞行器在世界空间中的坐标

首先根据Model矩阵和View矩阵计算ModelView矩阵MV_CPU，然后根据行器在世界空间中的坐标计算飞行器相对于观察者的坐标：

1

SpaceShuttle_Eye = MV_CPU * SpaceShuttle_World;

然后，将SpaceShuttle_Eye赋值给MV_CPU的平移分量（第四列前三个分量）：

1
2
3

MV_CPU[0, 3] = SpaceShuttle_Eye.x;
MV_CPU[1, 3] = SpaceShuttle_Eye.y;
MV_CPU[2, 3] = SpaceShuttle_Eye.z;

最后，将MV_CPU传递给GPU，得到MV_GPU，其中存在双精度向单精度的转换：

1

MV_GPU = MV_CPU;

下面采用真实数值来复现上述计算过程。飞行器在世界空间的坐标为

1

SpaceShuttle_World = (16678139.999999, 0.00000, 0.000000)

假设相机位于距离飞行器很近的某处

1
2
3
4
5

MV_CPU = [
0.000000  -0.976339   0.216245        -13.790775
0.451316  -0.192969  -0.871249   -7527123.004836
0.892363   0.097595   0.440638  -14883050.114944
0.000000   0.000000   0.000000          1.000000];

则飞行器相对于相机观察者的相对坐标为

1
2

SpaceShuttle_Eye = MV_CPU * SpaceShuttle_World;
// = (-13.790775, -11.572596, -95.070125)

将上述值插入MV_CPU的平移分量可以得到:

1
2
3
4
5

MV_CPU = [
0.000000  -0.976339   0.216245  -13.790775 
0.451316  -0.192969  -0.871249  -11.572596
0.892363   0.097595   0.440638  -95.070125
0.000000   0.000000   0.000000    1.000000];

最后将MV_CPU传递给GPU（着色器），得到MV_GPU。

可以看出，通过上述赋值插入，原本很大的平移分量显著的变小了，这样就可以消除抖颤。一旦视角移动，就需要重新计算MV_GPU，但是相比渲染成千上万的飞行器顶点而言，计算矩阵的资源消耗几乎可以忽略不计。

3. 相对于视角的渲染

一般而言，RTC技术已经足够达到cm级别的精度，只要模型的顶点距离模型中心小于131070m（实际上可能更小，但暂时未有时间分析测试）。但是在某些极端情况下，RTC技术仍然无法消除抖颤。

如果一个物体的顶点间隔超过131070米怎么办？当绘制卫星轨道线、物体之间的线和几何平面（如赤道平面）时，这并不少见。此时，没有一个可用的中心可以用来防止抖动。此时，需要采用一种改进的技术，即相对于视角的渲染（Rendering Relative to Eye, RTE）。

限于篇幅，此处不再继续展开，有需要可以参看参考文献。

4. 参考文献

[1] STK. Precisions, Precisions

Tutorial, Coding
simulation opengl
本文由作者按照 CC BY 4.0 进行授权