本文介绍了 OpenGL 中深度缓冲的概念,分析了在渲染巨型尺度场景下的深度冲突问题,并给出了采用对数深度缓冲的具体解决方案。
1. 深度缓冲
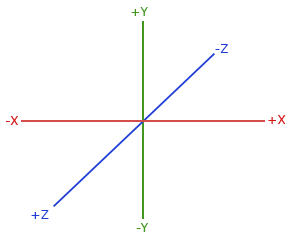
OpenGL是一个右手坐标系。简单来说,就是正x轴在你的右手边,正y轴朝上,而正z轴是朝向后方的。想象你的屏幕处于三个轴的中心,则正z轴穿过你的屏幕朝向你。在OpenGL中采用z坐标来描述深度信息。一般地,z轴的坐标原点在屏幕上,屏幕里为负轴,向外为正轴。OpenGL中的观察者为摄像机。一般地,摄像机的初始位置在OpenGL窗口的正中心。
OpenGL在绘制图形时,有些图形在前,有些图形在后,这时候就用到了z坐标。当然,并不一定图形1的z坐标大于图形2的z坐标,就说图形1会绘制在图形2的前面,因为图形的前后顺序决于我们的观察平面,即摄像机的位置。
深度缓冲(Depth Buffer)的原理就是把一个距离观察平面的深度值与窗口的每个像素相关联。在场景绘制时,在片段着色器中,如果遇到两个像素在屏幕上坐标相同的情况,在绘制前将会比较两者的深度(Z值),以判断两者之间谁离观察者更近。如果新的像素深度值大于旧的顶点,则以新像素覆盖原有像素;反之则放弃绘制新像素,保留原有像素。这个比较的过程称为深度测试(deepth testing)。
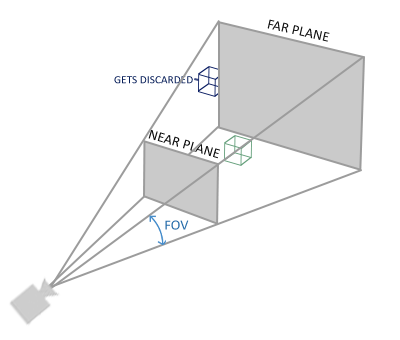
深度缓冲是由窗口系统自动创建的,它会以16、24或32位float的形式储存它的深度值。在大部分的系统中,深度缓冲的精度都是24位的。深度缓冲包含了一个介于0.0和1.0之间的深度值,它将会与观察者视角所看见的场景中所有物体的z值进行比较。观察空间的z值可能是投影平截头体的近平面(Near)和远平面(Far)之间的任何值。我们需要一种方式来将这些观察空间的z值变换到[0, 1]范围之间,其中的一种方式就是将它们线性变换到[0, 1]范围之间。下面这个(线性)方程将z值变换到了0.0到1.0之间的深度值[1]:
\[F_{depth}=\frac{z-near}{far-near}\]这里的$near$和$far$值是我们之前提供给投影矩阵设置可视平截头体的近平面(near plane)和远平面(far plane)。这个方程需要平截头体中的一个$z$值,并将它变换到了$[0, 1]$的范围中。可以看出,这个方程计算得到的深度值是线性的,然而,在实践中是几乎永远不会使用这样的线性深度缓冲(Linear Depth Buffer)的。
要想有正确的投影性质,需要使用一个非线性的深度方程,它是与$ 1/z$ 成正比的。它做的就是在$z$值很小的时候提供非常高的精度,而在$z$值很远的时候提供更少的精度。花时间想想这个:我们真的需要对1000单位远的深度值和只有1单位远的充满细节的物体使用相同的精度吗?线性方程并不会考虑这一点。
考虑一种深度缓冲与 $z$ 成反比的非线性方程如下:
\[F_{depth}=\frac{1/z-1/near}{1/far-1/near}\]由于深度值与$ 1/z$ 成正比,在1.0和2.0之间的z值将会变换至1.0到0.5之间的深度值,这就是一个float提供给我们的一半精度了,这在z值很小的情况下提供了非常大的精度,而在$z$值很大时,比如$z$在50.0和100.0之间的z值将会只占2%的float精度,这正是我们所需要的。也就是说,深度值很大一部分是由很小的$z$值所决定的,这给了近处的物体很大的深度精度(靠近相机的地方精度更高)。
2. 深度冲突
非线性深度缓冲在大多数场景中已经足够应用。然而,当两个模型间相距很近、或需要渲染大尺度场景(比如行星际场景)时,使用上述非线性深度缓冲会出现一个很严重的问题——深度冲突(z-fighting)。
比如在太阳系场景渲染中,一般需要同时渲染尺寸巨大距离遥远的行星(比如真实绕地飞行的月球)和体型相对很小的人造卫星。此时,需要设置很大的远平面值以保证极远处的物体能够得以渲染,设置很小的近平面值保证距离摄像机很近的物体也能够得以渲染。此时,若两个物体在距离摄像机较远,就没有足够的精度用于判断其远近。两个物体在同一个像素生成的渲染结果很容易对应到一个相同的z值,渲染器就不知道哪个物体在前,哪个物体在后,于是便开始“胡作非为”,这次让这个物体的这个像素在前面,下次让那个物体的这个像素在前面,于是模型的重叠部位便不停的闪烁起来。这便是深度冲突问题。
可采用以下措施来减缓深度冲突:
- 多边形偏移(Polygon_Offset):永远不要把多个物体摆得太靠近,以至于它们的一些三角形会重叠。通过在两个物体之间设置一个用户无法注意到的偏移值,你可以完全避免这两个物体之间的深度冲突。以放在地板上的一个箱子为例,我们可以将箱子朝上(沿着正y轴)稍微移动一点。箱子位置的这点微小改变将不太可能被注意到,但它能够完全减少深度冲突的发生。然而,这需要对每个物体都手动调整,并且需要进行彻底的测试来保证场景中没有物体会产生深度冲突。
- 近平面调整:尽可能将近平面设置远一些。在前面我们提到了精度在靠近近平面时是非常高的,所以如果我们将近平面远离观察者,我们将会对整个平截头体有着更大的精度。然而,将近平面设置太远将会导致近处的物体被裁剪掉,所以这通常需要实验和微调来决定最适合你的场景的近平面距离。
- 提高深度缓冲精度:牺牲一些性能,使用更高精度的深度缓冲。大部分深度缓冲的精度都是24位的,但现在大部分的显卡都支持32位的深度缓冲,这将会极大地提高精度。所以,牺牲掉一些性能,你就能获得更高精度的深度测试,减少深度冲突。
上述三个技术是最普遍也是很容易实现的抗深度冲突技术了。然而,上述措施只能减缓深度冲突问题,并不能够完全消除。还有一些更复杂的技术,但它们依然不能完全消除深度冲突:
- 多平截头体渲染(Multi-Frustums Rendering)
- 对数深度缓冲(Logarithmic Depth Buffer)
多边形平移需要手动设置每个可能发生深度冲突的模型,当模型很多时手动设置的工作量巨大。
多平截头体渲染需要根据所渲染的场景的尺寸,设置若干个平截头体,渲染工作量大,平截头体交汇处可能存在渲染问题。
3. 对数深度缓冲
对数深度缓冲(Logarithmic Depth Buffer)使得大尺寸场景(比如行星际尺寸)能够按照真实比例渲染,而几乎不会出现因精度不足导致的深度冲突现象。公式如下[2]:
公式
\[z= \left( 2\cdot\frac{log{(C \cdot w + 1)}}{log(C \cdot far + 1)} - 1 \right) \cdot w\]其中,$C$是常量。不同的$C$值会影响深度的精度;$w$是gl_Position.w。
相应的代码实现如下。顶点着色器中:
1
2
3
4
5
6
7
8
9
10
11
// vertex shader
out float logz;
in float far;
void main()
{
...
float C = 1;
float FC = 1.0 / log(far * C + 1);
logz = log(gl_Position.w * C + 1) * FC;
gl_Position.z = (2 * logz - 1) * gl_Position.w;
}
片段着色器中:
1
2
3
4
5
6
7
// fragment shader
in float logz;
void main()
{
...
gl_FragDepth = logz;
}
可对上述代码进行进一步优化[3]:
- 使用 log2 代替 log: 因为在着色器中,log 是基于 log2 实现的,因此直接使用 log2 避免额外的计算;
- 避免裁剪问题: 当数值小于等于 0 时,log 函数没有定义。当三角形的某个顶点超出相机平面时 (≤ -1),会导致该三角形在裁剪之前就被整个删除。将 log 函数的输入值限定在
max(1e-6, 1.0 + gl_Position.w)可以避免这个问题; - 移除常数
C:常数C用来调整近端的精度,但因为一般情况下C=1时的精度已经足够使用,因此将其移除。
最终优化的代码如下。顶点着色器中:
1
2
3
4
5
6
7
8
9
10
11
12
13
// vertex shader
out float flogz;
out float Fcoef;
in float far;
...
void main()
{
...
Fcoef = 2.0 / log2(far + 1.0);
flogz = 1.0 + gl_Position.w;
gl_Position.z = log2(max(1e-6, flogz)) * Fcoef - 1.0;
gl_Position.z *= gl_Position.w;
}
片段着色器中:
1
2
3
4
5
6
7
8
9
// vertex shader
out float logz;
in float far;
...
void main()
{
...
gl_FragDepth = log2(flogz) * Fcoef * 0.5;
}
值得注意的是,在某些极端场景下[4],单纯采用对数深度缓冲仍然会存在深度冲突(如从极远的距离观看极大尺寸的三角面)。此时可以采取“多平截头体渲染+对数深度缓冲”二者混合的模式(Hybrid Multi-Frustum Logarithmic Depth Buffer)来渲染场景。
4. 参考文献
[1] LearnOpenGL. Depth Testing
[2] Outerra. Maximizing Depth Buffer Range and Precision
[3] Outerra. Logarithmic depth buffer optimizations & fixes
[4] Cesium. Hybrid Multi-Frustum Logarithmic Depth Buffer
[5] sirlis. Logarithmic Depth Buffer in OpenGL with glad/glfw