本文介绍了 1993 年发表的自适应网络模糊推理系统(ANFIS),Adaptive-Network-Based Fuzzy Inference System。
1. 基础知识
1.1. 模糊推理系统
Fuzzy Inference System(FIS),由五个功能模块组成:
- 包含若干模糊if-then规则的规则库;
- 定义关于使用模糊if-then规则的模糊集的隶属函数的数据库;
- 在规则上的执行推理操作的决策单元;
- 将明确输入转化为与语言价值匹配的程度的模糊界面;
- 将推理得到的模糊结果转化为明确输出的去模糊界面。
通常,1、2被联合称为知识库。
1.2. 自适应网络
自适应网络是一个由节点和连接节点的定向链路组成的多层前馈网络,其中每个节点对传入的信号以及与此节点相关的一组参数执行一个特定的功能(节点函数)。自适应网络的结构中包含有参数的方形节点和无参数的圆形节点,自适应网络的参数集是每个自适应节点的参数集的结合。他们的输出依赖于这些节点相关的参数,学习规则指定如何更改这些参数。
Jyh-Shing Roger Jang 于 1993 年发表的《ANFIS : Adaptive-Network-Based Fuzzy Inference System》。当时对于处理模糊不确定系统,使用传统数学工具的系统建模并不能得到令人满意的效果。考虑采用模糊if-then规则的模糊推理系统不需要精确的定量分析就可以对人的知识和推理过程进行定性建模,作者提出了一种基于自适应网络的模糊推理系统。
1.3. ANFIS 结构
ANFIS的模型结构由自适应网络和模糊推理系统合并而成,在功能上继承了模糊推理系统的可解释性的特点以及自适应网络的学习能力,能够根据先验知识改变系统参数,使系统的输出更贴近真实的输出。
为简单起见,假定所考虑的模糊推理系统有2个输入x和y,单个输出z。对于一阶 Takagi-Sugeno 模糊模型,如果具有以下2条模糊规则
- rule 1: if $x$ is $A_1$ and $y$ is $B_1$ then $f_1=p_1x+q_1y+r_1$
- rule 2: if $x$ is $A_2$ and y is $B_2$ then $f_2=p_2x+q_2y+r_2$
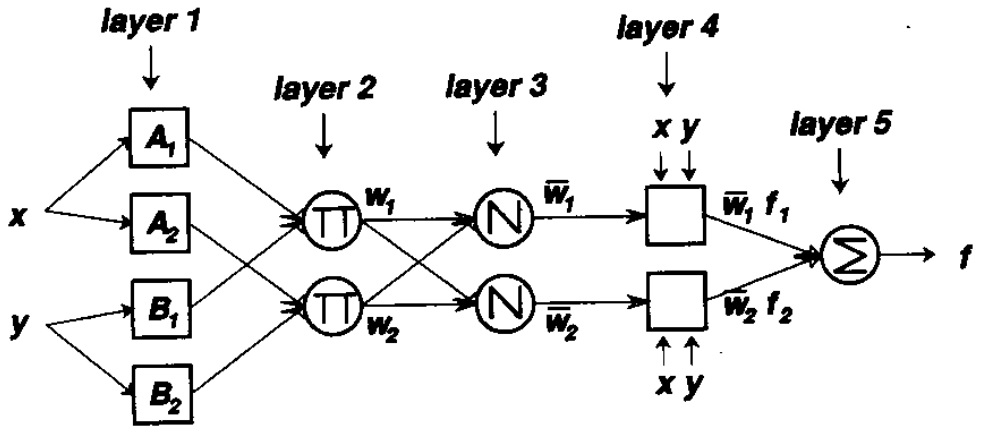
那么该一阶T-S模糊推理系统的ANFIS网络结构如图所示
输入x,y在第一层进行模糊化,模糊化的方法:用隶属函数(menbership functions,MFs,一般为钟形函数,钟形函数参数为前向参数)对输入特征x,y进行模糊化操作,得到一个[0,1]的隶属度(menbership grade),通常用mu表示。
在第二层,每个特征的隶属度mu相乘得到每个规则的触发强度(firing strength)。
第三层将上一层得到的每条规则的触发强度做归一化,表征该规则在整个规则库中的触发比重,即在整个推理过程中使用到这条规则的程度(用概率理解)。
第四层计算规则的结果,一般由输入特征的线性组合给出(假设输入有n个特征,$f_i=c_0+c_1x_1+c_2x_2+…+c_nx_n$。$c_0,c_1,…,c_n$为后向参数)。
第五层去模糊化得到确切的输出,最终的系统输出结果为每条规则的结果的加权平均(权重为规则的归一化触发程度,理解为计算期望)。
ANFIS is a way of presenting a fuzzy inference system (FIS) as a series of numeric layers so that it can be trained like a neural net.
The canonical reference is the original paper by Jyh-Shing Roger Jang:
- Jang, J.-S.R. (1993). “ANFIS: adaptive-network-based fuzzy inference system”. IEEE Transactions on Systems, Man and Cybernetics. 23 (3): 665–685. doi:10.1109/21.256541
Note that it assumes a Takagi Sugeno Kang (TSK) style of defuzzification rather than the more usual Mamdani style.
1.4. ANFIS 学习算法
文章W中给出的学习算法(参数更新方法)为 LSE-GD 混合学习算法。即更新参数同时在前向传递和反向传递中进行。
在正向传播中,我们固定前向参数,在输入传递到第四层时,通过最小二乘估计(least square estimate,LSE)更新后向参数,在这种前向参数(隶属度函数的参数)固定的前提下,得到的后向参数(第四蹭线性组合参数)估计是最优的,这样,混合学习算法比单纯的GD算法要快很多。
2. 程序文件组成
ANFIS(https://github.com/jfpower/anfis-pytorch )
The ANFIS framework is mainly in three files:
-
anfis.py This is where the layers of the ANFIS system are defined as Torch modules.
-
membership.py At the moment I only have Bell and Gaussian membership functions, but any others will go in here too.
-
experimental.py The experimental infrastructure to train and test the FIS, and to plot some graphs etc.
There are then some runnable examples:
-
jang_examples.py these are four examples from Jang’s paper (based partly on the details in the paper, and particle on the example folders in his source code distribution).
-
vignette_examples.py these are three examples from the Vignette paper. Two of these use Gaussians rather than Bell MFs.
3. membership.py
定义了隶属度函数。
3.1. make_anfis()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def make_anfis(x, num_mfs=5, num_out=1, hybrid=True):
'''
Make an ANFIS model, auto-calculating the (Gaussian) MFs.
I need the x-vals to calculate a range and spread for the MFs.
Variables get named x0, x1, x2,... and y0, y1, y2 etc.
'''
num_invars = x.shape[1]
minvals, _ = torch.min(x, dim=0)
maxvals, _ = torch.max(x, dim=0)
ranges = maxvals-minvals
invars = []
for i in range(num_invars):
sigma = ranges[i] / num_mfs
mulist = torch.linspace(minvals[i], maxvals[i], num_mfs).tolist()
invars.append(('x{}'.format(i), make_gauss_mfs(sigma, mulist)))
outvars = ['y{}'.format(i) for i in range(num_out)]
model = AnfisNet('Simple classifier', invars, outvars, hybrid=hybrid)
return model
输入 x 的列数作为输入状态量的个数,求 x 跨行间比较的最大值和最小值(即沿着每列求最大值和最小值) minvals, maxvals,即可得到输入各个状态量的取值范围 ranges。
num_mfs 为隶属度函数的个数。对于每个输入状态量,采用取值范围除以 num_mfs 来初始化 sigma,采用在取值范围内均匀取 num_mfs 个点来初始化 mulist。用得到的 sigma, mulist 来初始化高斯隶属度函数 make_gauss_mfs()。
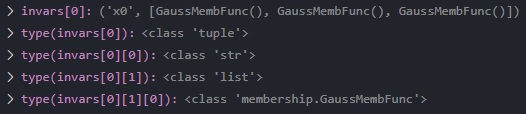
最终,将得到的隶属度函数,与一个字符串 'x{}'.format(i) 一起,组成一个元组(tuple),添加到列表 invars 中作为后续建立网络的输入。假设输入状态量维度(列数)为2,则 invars 的成员为
1
2
invars[0] = ['x0', [GaussMembFunc(), GaussMembFunc(), GaussMembFunc()]]
invars[1] = ['x1', [GaussMembFunc(), GaussMembFunc(), GaussMembFunc()]]
outvars 列表通过遍历输出状态量的维度来建立,是一个字符串列表。假设输出状态量维度为3,则 outvars 的成员为
1
outvars = ['y0', 'y1', 'y2']
最后,将 invars 和 outvars 作为参数传入 AnfisNet() 建立 ANFIS 网络。转到 AnfisNet() 查阅。
3.2. make_gauss_mfs()
1
2
3
def make_gauss_mfs(sigma, mu_list):
'''Return a list of gaussian mfs, same sigma, list of means'''
return [GaussMembFunc(mu, sigma) for mu in mu_list]
make_gauss_mfs 输入 sigma, mulist ,根据 mulist 的个数(也就是之前 make_anfis() 函数中传入的隶属度函数的个数 num_mfs),调用 GaussMembFunc(),返回一个成员为 membership.GaussMembFunc 类型的列表。
3.3. GaussMemFunc()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class GaussMembFunc(torch.nn.Module):
'''
Gaussian membership functions, defined by two parameters:
mu, the mean (center)
sigma, the standard deviation.
'''
def __init__(self, mu, sigma):
super(GaussMembFunc, self).__init__()
self.register_parameter('mu', _mk_param(mu))
self.register_parameter('sigma', _mk_param(sigma))
def forward(self, x):
val = torch.exp(-torch.pow(x - self.mu, 2) / (2 * self.sigma**2))
return val
def pretty(self):
return 'GaussMembFunc {} {}'.format(self.mu, self.sigma)
该函数包括 mu, sigma 两个可反向求导的参数,同时在 foward 中定义了函数的前向传播表达式并返回函数值 val,即一个高斯函数
4. anfis.py
定义了 ANFIS 的层。
4.1. AnfisNet()
定义了 5 层的 ANFIS 网络类容器。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class AnfisNet(torch.nn.Module):
'''
This is a container for the 5 layers of the ANFIS net.
The forward pass maps inputs to outputs based on current settings,
and then fit_coeff will adjust the TSK coeff using LSE.
'''
def __init__(self, description, invardefs, outvarnames, hybrid=True):
super(AnfisNet, self).__init__()
self.description = description
self.outvarnames = outvarnames
self.hybrid = hybrid
varnames = [v for v, _ in invardefs]
mfdefs = [FuzzifyVariable(mfs) for _, mfs in invardefs]
self.num_in = len(invardefs)
self.num_rules = np.prod([len(mfs) for _, mfs in invardefs])
if self.hybrid:
cl = ConsequentLayer(self.num_in, self.num_rules, self.num_out)
else:
cl = PlainConsequentLayer(self.num_in, self.num_rules, self.num_out)
self.layer = torch.nn.ModuleDict(OrderedDict([
('fuzzify', FuzzifyLayer(mfdefs, varnames)),
('rules', AntecedentLayer(mfdefs)),
# normalisation layer is just implemented as a function.
('consequent', cl),
# weighted-sum layer is just implemented as a function.
]))
在函数的初始化中,首先对 invardefs 进行拆分,前面已知
1
2
invardefs[0] = ['x0', [GaussMembFunc(), GaussMembFunc(), GaussMembFunc()]]
invardefs[1] = ['x1', [GaussMembFunc(), GaussMembFunc(), GaussMembFunc()]]
这里将其拆分为两个部分:varnames 和 mfdefs
varnames = ['x0', 'x1']为invardefs的前半部分mfdefs是一个列表,列表的成员为FuzzifyVariable类(anfis.FuzzifyVariable),类的形参输入为invardefs的后半部分,即隶属度函数列表,经过类初始化后得到如下形式的列表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
mfdefs =
[FuzzifyVariable(
(mfdefs): ModuleDict(
(mf0): GaussMembFunc()
(mf1): GaussMembFunc()
(mf2): GaussMembFunc()
)
),
FuzzifyVariable(
(mfdefs): ModuleDict(
(mf0): GaussMembFunc()
(mf1): GaussMembFunc()
(mf2): GaussMembFunc()
)
)]
跳转到 FuzzifyVariable() 类 查阅更多。
self.num_rules 将所有隶属度函数个数做元素积,这里
1
2
[len(mfs) for _, mfs in invardefs] = [3,3]
np.prod[3,3] = 9
然后将self.num_in,self.num_rules,self.num_out 作为参数传给 PlainConsequentLayer() 类。 最终,形成一个三层网络结构 self.layer。
其中,self.num_in,self.num_rules 在实例化 AnfisNet 时确定,而 self.num_out 是通过下面代码根据 self.outvarnames 的长度得到的
1
2
3
@property
def num_out(self):
return len(self.outvarnames)
其中,@property 装饰器[1] 把 num_out 的 getter 方法变成属性,但是没有定义 num_out.setter 方法,从而将 num_out 变为一个 私有的只读属性。该属性无法在外部进行更改,而是在实例化 AnfisNet 时根据 outvarnames 自动确定的。
与之相反,coeff 定义时既包括 @property 又包括 @coeff.setter 方法,那么 coeff 就可以在外部进行赋值更改。
1
2
3
4
5
6
7
@property
def coeff(self):
return self.layer['consequent'].coeff
@coeff.setter
def coeff(self, new_coeff):
self.layer['consequent'].coeff = new_coeff
这样做的好处是可以在赋值时进行一些复杂的操作,比如上述代码中的 self.layer['consequent'].coeff = new_coeff 操作,或者如参考文献 [1] 中的取值类型和范围的限定报错提示操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def fit_coeff(self, x, y_actual):
'''
Do a forward pass (to get weights), then fit to y_actual.
Does nothing for a non-hybrid ANFIS, so we have same interface.
'''
if self.hybrid:
self(x)
self.layer['consequent'].fit_coeff(x, self.weights, y_actual)
def input_variables(self):
'''
Return an iterator over this system's input variables.
Yields tuples of the form (var-name, FuzzifyVariable-object)
'''
return self.layer['fuzzify'].varmfs.items()
def output_variables(self):
'''
Return an list of the names of the system's output variables.
'''
return self.outvarnames
def extra_repr(self):
rstr = []
vardefs = self.layer['fuzzify'].varmfs
rule_ants = self.layer['rules'].extra_repr(vardefs).split('\n')
for i, crow in enumerate(self.layer['consequent'].coeff):
rstr.append('Rule {:2d}: IF {}'.format(i, rule_ants[i]))
rstr.append(' '*9+'THEN {}'.format(crow.tolist()))
return '\n'.join(rstr)
def forward(self, x):
'''
Forward pass: run x thru the five layers and return the y values.
I save the outputs from each layer to an instance variable,
as this might be useful for comprehension/debugging.
'''
self.fuzzified = self.layer['fuzzify'](x)
self.raw_weights = self.layer['rules'](self.fuzzified)
self.weights = F.normalize(self.raw_weights, p=1, dim=1)
self.rule_tsk = self.layer['consequent'](x)
# y_pred = self.layer['weighted_sum'](self.weights, self.rule_tsk)
y_pred = torch.bmm(self.rule_tsk, self.weights.unsqueeze(2))
self.y_pred = y_pred.squeeze(2)
return self.y_pred
4.2. FuzzifyVariable 类
1
2
3
4
5
6
7
8
9
10
11
12
class FuzzifyVariable(torch.nn.Module):
'''
Represents a single fuzzy variable, holds a list of its MFs.
Forward pass will then fuzzify the input (value for each MF).
'''
def __init__(self, mfdefs):
super(FuzzifyVariable, self).__init__()
if isinstance(mfdefs, list): # No MF names supplied
mfnames = ['mf{}'.format(i) for i in range(len(mfdefs))]
mfdefs = OrderedDict(zip(mfnames, mfdefs))
self.mfdefs = torch.nn.ModuleDict(mfdefs)
self.padding = 0
该类的初始化步骤如下:
- 通过
isinstance()判断输入的mfdefs是否是列表; - 如果是,则给
mfdefs中的每个成员取名为mf{}.format(i),并形成列表mfnames; - 通过
zip()将mfnames和mfdefs组合成一个成员为元组的列表(a list of tuples); - 将上述列表传入
OrderDict得到有序字典mfdefs mfdefs传入torch.nn.ModuleDict()得到self.mfdefs。
1
2
3
4
5
6
7
8
9
10
mfdefs = OrderedDict([
('mf0', GaussMembFunc()),
('mf1', GaussMembFunc()),
('mf2', GaussMembFunc())
])
self.mfdefs = ModuleDict(
(mf0): GaussMembFunc()
(mf1): GaussMembFunc()
(mf2): GaussMembFunc()
)
torch.nn.ModuleDict() 自动将 mfdefs 注册为参数(可被反向传播且可被迁移到GPU上加速计算)。注意,传入 torch.nn.ModuleDict() 的类必须是 torch.nn.Module 的子类。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
@property
def num_mfs(self):
'''Return the actual number of MFs (ignoring any padding)'''
return len(self.mfdefs)
def members(self):
'''
Return an iterator over this variables's membership functions.
Yields tuples of the form (mf-name, MembFunc-object)
'''
return self.mfdefs.items()
def pad_to(self, new_size):
'''
Will pad result of forward-pass (with zeros) so it has new_size,
i.e. as if it had new_size MFs.
'''
self.padding = new_size - len(self.mfdefs)
def fuzzify(self, x):
'''
Yield a list of (mf-name, fuzzy values) for these input values.
'''
for mfname, mfdef in self.mfdefs.items():
yvals = mfdef(x)
yield(mfname, yvals)
def forward(self, x):
'''
Return a tensor giving the membership value for each MF.
x.shape: n_cases
y.shape: n_cases * n_mfs
'''
y_pred = torch.cat([mf(x) for mf in self.mfdefs.values()], dim=1)
if self.padding > 0:
y_pred = torch.cat([y_pred,
torch.zeros(x.shape[0], self.padding)], dim=1)
return y_pred
4.3. ConsequentLayer 类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class ConsequentLayer(torch.nn.Module):
'''
A simple linear layer to represent the TSK consequents.
Hybrid learning, so use MSE (not BP) to adjust coefficients.
Hence, coeffs are no longer parameters for backprop.
'''
def __init__(self, d_in, d_rule, d_out):
super(ConsequentLayer, self).__init__()
c_shape = torch.Size([d_rule, d_out, d_in+1])
self._coeff = torch.zeros(c_shape, dtype=dtype, requires_grad=True)
@property
def coeff(self):
'''
Record the (current) coefficients for all the rules
coeff.shape: n_rules * n_out * (n_in+1)
'''
return self._coeff
@coeff.setter
def coeff(self, new_coeff):
'''
Record new coefficients for all the rules
coeff: for each rule, for each output variable:
a coefficient for each input variable, plus a constant
'''
assert new_coeff.shape == self.coeff.shape, \
'Coeff shape should be {}, but is actually {}'\
.format(self.coeff.shape, new_coeff.shape)
self._coeff = new_coeff
4.4. PlainConsequentLayer 类
继承自 ConsequentLayer 类
5. 参考文献
[1] luyuze95 只顾风雨兼程. python中@property装饰器的使用.
[2] Rudolf Kruse. Fuzzy neural network.
[3] Milan Mares. Fuzzy Sets.
[4] L.A. Zadeh. Fuzzy sets.
[5] Pranav Gajjewar. Understanding Fuzzy Neural Network using code and animation