本文介绍了天文学中基本的时间和历法知识。

1. 背景

1.1. 国际地球自转和参考系服务

国际地球自转和参考系服务（International Earth Rotation and Reference System, IERS）（官网：https://www.iers.org/IERS/EN/Home/home_node.html ）的主要目标是通过提供国际陆空参考系统的入口来为天文学、测地学和地球物理学的研究团体服务。该网站提供了有关国际地球自转服务中心的任务、机构设置、成员以及相关产品的详细信息，同时还提供了通向其数据库和公告中的观测数据与研究结果的入口。

国际地球自转服务(International Earth Rotation Service-简称IERS)由国际大地测量学和地球物理学联合会及与国际天文学联合会联合创办，用以取代国际时间局(BIH)的地球自转部分和原有的国际极移服务(IPMS)。

1.2. 国际天文学联合会

国际天文学联合会（International Astronomical Union, IAU）（官网：https://www.iau.org/ ）是世界各国天文学术团体联合组成的非政府性学术组织，其宗旨是组织国际学术交流，推动国际协作，促进天文学的发展。国际天文学联合会于1919年7月在布鲁塞尔成立。天文学联盟有73个成员国，其中包括专业天文学研究达到较高程度的大多数国家。天文学联盟的一个主要从事地面和空间天文学各学科的10528 多名成员的直接参与。

2. 时间

2.1. 太阳时

太阳时（Solar time）是一种以地球自转为基础的时间计量系统，以地球相对于太阳的自转周期为基准，用太阳对于该地子午圈的时角来量度，基础时间单位为太阳日。太阳时的初始时刻，以太阳在该地下中天瞬间作为太阳时零时。太阳时的类型分别为真太阳时（apparent solar time或sundial time）和平太阳时（mean solar time或clock time）。

地球表面活动的人们，习惯以太阳在天球上的位置来确定时间，因此将太阳连续两次经过上中天的时间间隔称为真太阳日，地方真太阳日12时为太阳在该地上中天瞬时。然而，地球绕太阳公转运动的轨道是椭圆，太阳位于该椭圆的一个焦点上，所以地球在轨道上做的是不等速运动，真太阳周日视运动的速度是不均匀的，不易选做计时单位。

为了得到以真太阳周日视运动为基础而又克服其不均匀性的时间计量系统，人们引入了平太阳日的概念。天文学上假定由一个太阳（平太阳）在天赤道上（而不是在黄赤道上）作等速运行，其速度等于运行在黄赤道上真太阳的平均速度，这个假想的太阳连续两次上中天的时间间隔，叫做一个平太阳日。这也相当于把一年中真太阳日的平均称为平太阳日，并且把1/24平太阳日取为1平太阳时。人们日常生活中使用的“日”和“时”，就是平太阳日和平太阳时的简称。平太阳时的基本单位是平太阳日，1平均太阳日等于24平均太阳小时，1平均太阳小时等于86400平均太阳秒。

2.2. 恒星时

恒星时（Sidereal time）是一种以地球自转为基础的时间计量系统，以地球相对于恒星的自转周期为基准。恒星时基础时间单位为恒星日，将春分点相继两次经过上中天的时间间隔称为恒星日，并以春分点在该地上中天的瞬间作为这个计量系统的起点，即恒星时零时。

由于地球的章动，春分点在天球上并不固定，而是以18.6年的周期围绕着平均春分点摆动。因此恒星时又分为真恒星时和平恒星时。真恒星时是通过直接测量子午线与实际的春分点之间的时角获得的，平恒星时则忽略了地球的章动。真恒星时与平恒星时之间的差异最大可达约0.4秒。

受到地球公转的影响，一个恒星日的长度要比一个太阳日的长度略短，一个平恒星日约等于23时56分4.09秒平太阳时。任何给定地点的恒星时将比当地民用时间每24小时增加约4分钟，直到一年过去后，与过去的太阳日数相比，恒星时要多一个恒星日。

2.3. 格林尼治标准时间（GMT）

格林尼治标准时间（Greenwich Mean Time, GMT）是英国伦敦格林尼治当地的平太阳时，以平子夜作为0时开始。

历史上格林尼治标准时间的定义和计算较为混乱。比如，天文学领域常以正午12时作为格林尼治标准时间开始的计算方法，也有地方将其作为协调世界时UTC+0的别名。在导航领域，GMT常常被认为与UT1等同。正因为如此混乱的定义与使用，格林尼治标准时间不可以被单独作为精确的时间标准。

1935年，国际天文学联合会推荐使用“世界时”一词，作为比格林威治标准时间更精确的术语，用以指代以平子夜作为0时开始的格林尼治标准时间。但在一些应用中（英国广播公司国际频道、英国气象局、英国皇家海军、中东广播中心等），格林威治标准时间一词在民用计时方面一直沿用至今。

2.4. 世界时（UT）

世界时（Universal Time, UT）是一种以地球自转为基础的时间计量系统。世界时理论上通过观测太阳的日运动来定义，但由于精确观测太阳十分困难，因此往往退而求其次，使用长基线干涉测量法确定遥远类星体位置、对月球和人造卫星进行激光测距、以及对GPS卫星进行轨道确定来计算。世界时包含四个版本，区别在于包含不同的修正项调整来接近太阳时。世界时的四个版本定义如下：

UT0：UT0是通过天文太观测恒星或河外射电源的日运动以及对月球和人造地球卫星的测距观测确定的世界时。UT0不包含任何校正，并且已不再常用；
UT1：UT1是在UT0的基础上增加地球极移修正后得到的，是世界时的主要形式。在确定UT0时，假定天文台的位置在地球参考系（如国际地球参考系）中坐标固定。但是，地球自转轴的位置并不固定，而是在地球表面漂移，即极移。因此，定义UT1时考虑并增加了极移修正；
UT1R：UT1R是在UT1的基础上增加周期性潮汐变化修正后得到的，它包括62个修正项，周期从5.6天到18.6年不等；
UT2：是在UT1的基础上增加季节性变化修正后得到的，已经不再常用。

世界时曾长期被认为是稳定均匀的时间计量系统，历史上得到广泛应用。后文如无特别说明，世界时均指的是UT1。

2.5. 原子时（TAI）

1955年铯原子钟的发明，提供了一种比天文观测更稳定且更方便的授时机制。1967年第13届国际计量大会上通过一项决议，给出了新的国际单位“秒”的定义，一秒为铯-133原子基态两个超精细能级间跃迁辐射振荡9192631770周所持续的时间，其稳定度可以达到{10}^{-14}以上。

原子时（Temps Atomique International，TA或TAI）就是根据上述秒的定义确定的一种新的国际参照时标，其初始时间为1958年1月1日世界时0时，即在这一瞬间TA和UT1重合。目前，国际原子时由国际计量局收集50多个国400多个实验室的原子钟比对和时号发播资料进行综合处理后建立，可参考：

Bureau International des Poids et Mesures (BIPM) Time Department”. Report of the International Association of Geodesy 2011-2013. http://iag.dgfi.tum.de/fileadmin/IAG-docs/Travaux2013/08_BIPM.pdf

各个国家为了满足各个行业对实时时间信号的需要，建立各国的实时的时间尺度——地方原子时TA（k），k为实验室代号。TA（JATC）是由国家授时中心联合国内其他单位成立综合原子时委员会（Joint Atomic Time Commission）负责建立的独立地方原子时尺度，1987年起参加国际原子时TAI计算，从未中断。

2.6. 协调世界时（UTC）

C协调世界时（英语Coordinated Universal Time，法语Temps Universel Coordonné，二者妥协后简称UTC）是最主要的世界时间标准，其以原子时秒长为基础，作为格林尼治标准时间的替代，在时刻上尽量接近于格林尼治标准时间（也即世界时UT1）。虽然国际原子时更为精密，但在实际应用中人们希望时间系统更加接近世界时，因为其更加贴近人们日常感官上的时间流逝。因此，1972年提出协调世界时的折中时标，它既保持时间尺度的均匀性，又能近似地反映地球自转的变化。协调世界时由国际计量局（Bureau International des Poids et Mesures，BIPM）维护。

由于协调世界时与世界时的时间单位的不一致性，二者之差逐年积累，便采用跳秒（闰秒）的方法使二者的时刻相差不超过1秒。1972年，国际计量大会决定，当世界时与协调世界时之间时刻相差超过0.9秒时，就在协调世界时上加上或减去1秒，以尽量接近世界时，这就是闰秒。闰秒一般在12月31日或6月30日末加入。具体日期由国际地球自转服务组织（1ERS）安排井通告。由于几十年来地球自转正在逐渐变慢，国际计时机构一共实行了二十多次闰秒操作，确保我们协调世界时与地球自转速度相匹配，截至目前协调世界时已经正闰秒37秒。国家授时中心每月均会发布《时间频率公报》，其中包含协调世界时和原子时之间的时差，可在知网查看和下载【2】。以2021年12月31日为例，原子时和协调世界时之差为

\[\begin{aligned} &\rm UTC = UT1 + DUT1 = UT1+37s+63.901us\\ &(DUT1 < 0.9s) \end{aligned}\]

经过闰秒调整之后，协调世界时与世界时的差值称为DUT1，可以从美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）获得【1】，以2021年12月31日为例，差值为

\[\rm DUT1 = UT1-UTC = -110.4ms\]

也可以通过IERS官网保持更新的 Bulletin D 来查询最新的DUT1，以2021年12月31日为例，查询得到的结果为

\[\rm DUT1 = -0.1s\]

UTC与TAI的差值由IERS保持更新的 Bulletin C 来查询，以2021年12月31日为例，查询得到的结果为

\[\rm UTC-TAI=-37s\]

IERS Bulletin 发布网址： https://www.iers.org/IERS/EN/Publications/Bulletins/bulletins.html

北京时间为 $\rm UTC^{+8}$，与 $\rm UTC$ 的关系为

\[\rm UTC^{+8} = UTC + 8\]

2.7. GPS时间

GPS时间，也就是GPS原子时，参照美国海军天文台（United States Naval Observatory，USNO）的主时钟（Main Clock，MC）为基准。GPS时间的初始原点定义为在1980年1月6日0点与世界协调时相等，以后按原子时秒长累积计时且不包含闰秒。GPS时间跟UTC时间之差为秒的整倍数。GPS导航采用GPS时间，计量单位为GPS周和GPS秒。

由于1980年1月6日，协调世界时已经正闰秒19秒，因此截至目前（2021年12月31日）GPS时与世界协调时的时差为18秒。

2.8. 历书时

前面所述的太阳时、恒星时和世界时都是以地球自转为基础的时间计量系统。然而，地球自转一直在变缓，而且变缓规律难以预测，这使地球自转为基础的时间计量系统是一种不均匀的时间系统。但是，天文学家们需要一个更加均匀的时间标尺来进行精确计算（虽然UTC是一种均匀的时间计量系统，但它需要随时通过跳秒来保持与世界时的一致，这种不连续性使其无法用于天文计算）。1958年，国际天文学联合会决议，自1960年开始用历书时（Ephemeral Time，ET）代替世界时作为基本的时间计量系统，并规定世界各国天文年历的太阳、月球、行星历表，都以历书时为准进行计算。历书时基于地球公转定义，历书时秒的定义为1900年1月0日12时正回归年长度的1/31556925.9747（也就是平太阳时的1秒）。历书时可以通过对太阳、月球或其他行星的观测二获得。相比于地球自转，地球公转要稳定的多，但仍然不是严格均匀的运动，只能达到 $10^{-10}s$ 级别。

由于历书时的测定精度较低，1967年起已用原子时代替历书时作为基本的时间计量系统，但当时在天文历表上仍用历书时。1976年第十六届国际天文学联合会决议，从1984年起天文计算和历表上所用的时间单位，也都以原子时秒为基础（力学时）。

2.9. 力学时

由于历书时所用的基准地球运动的理论框架是牛顿力学，根据广义相对论可知，在以太阳为中心的坐标系和以地球为中心的坐标系中时间将会不同。因此，在1979年国际天文学联合会第17届大会分别定义了两个新的相对论时间标准：太阳系质心力学时（Barycentric Dynamical Time，TDB）和地球力学时（Terrestrial Dynamical Time，TDT）。质心力学时和地球力学时可以看作是历书时分别在两个坐标系中的继承。国际天文学联合会（IAU）规定TDT与TDB之间的平均钟速相等，二者之差不存在长期项，只存在周期性差异，且这种周期性差异是由于相对论效应而引起的。

TDT主要用于给出天体在底薪坐标系中的视位置，计算天体在地心坐标系中的方程中的时间变量也应该使用TDT。月球、太阳、行星的历表则以TDB为时间变量，岁差、章动计算公式也是以TDB为时间变量的。

TDB和TDT的引入并没有完全解决时间基准面临的问题，反而出现了很多争议，如：1）对“动力学”（Dynamical）一词如何解释？；2）TDT被定义为“TAI理想化形式”的时候是坐标时，但在某些情况下又被解释成是在地心的本征时；等等。

2.10. 地球时

为了解决引入 $\rm TDB$ 和 $\rm TDT$ 存在的问题，1991年国际天文学联合会第21届大会做出决议，定义地球时（Terrestrial Time，TT）取代 $\rm TDT$ 作为视地心历表的时间变量，同时定义了相对论框架下的太阳系之心天球参考系（BCRS）和地球质心天球参考系（GCRS）。地球时的秒长与原子时相同，时间原点定义为在原子时1977年1月1日00:00:00瞬间，地球时的读数为1977年1月1日00:00:32.184。 $\rm TT$ 与 $\rm TDT$ 的秒长和时间原点相同，可以认为是等价的。不过TT更加明确为一种坐标时，从而解决了TDT定义在时间性质方面的不确定性。即

\[\rm TT = TAI + 32.184s\]

$\rm TT$ 与 $\rm UT1$ 之间的时差 $\rm \Delta T$ 可有美国海军天文台发布的historic_deltat.data、deltat.data、deltat.preds三个数据文件提供（包括1657-2023年间的具体数值），且定期对数据进行更新。还可以由IERS发布的 EOP 08 C04 模型中的 $\rm DUT1$ 、IERS Bulletin C 中的 LeapSecond 数据经计算后得到

\[\rm \Delta T=TT-UT1=LeapSecond+32.184-DUT1\]

$\rm TDB$ 和 $\rm TT$ 之间没有长期漂移，只有周期项变化，即

\[\rm TDB = TT + 0.001658sin(M)+0.000014sin(2M)+\frac{V_e(X-X_0)}{c^2}\]

其中，$M$ 为地球绕日公转的平近点角，$V_e$ 为地球质心在太阳系质心坐标系中的公转速度矢量，$X_0$ 为地心在太阳系质心坐标系中的位置矢量，$X$ 为地面钟在太阳系质心坐标系中的位置矢量，$X-X_0$ 实际上就是在太阳系质心坐标系下地面钟相对于地心的位置矢量，$c$ 为真空光速。

可以采用 $\rm TT$ 代替 $\rm TDB$，因为二者之间的差带来的影响可以忽略不计。所以虽然 JPL 星历使用 TDB ，但是可以直接用 TT 来代替。

参考：赵玉晖《深空探测中的轨道设计和轨道力学》

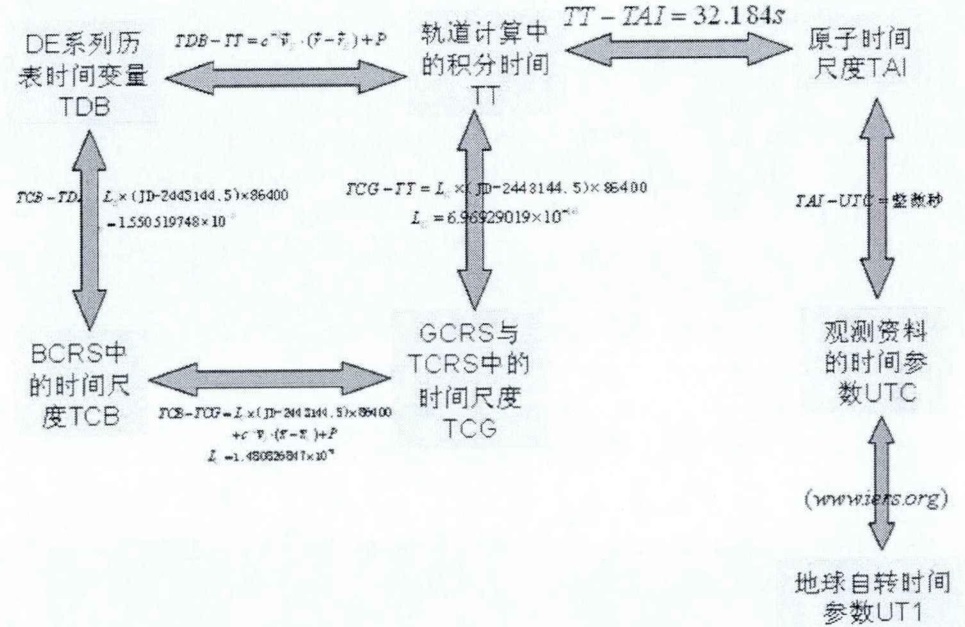
2.11. 各时间的转换关系

参考：赵玉晖《深空探测中的轨道设计和轨道力学》

3. 历法

3.1. 儒略历（Julian calendar）

儒略历（Julian calendar）是由罗马共和国独裁官儒略·凯撒采纳埃及亚历山大的数学家兼天文学家索西琴尼的计算后，于公元前45年1月1日起执行的取代旧罗马历法的一种历法。

儒略历中，一年被划分为12个月，大小月交替；四年一闰，平年365日，闰年366日为在当年二月底增加一闰日，年平均长度为365.25日。

由于实际使用过程中累积的误差随着时间越来越大，1582年教皇格里高利十三世颁布、推行了以儒略历为基础改善而来的格里历，即公历。

3.2. 格里高利历（Gregory Calendar）

是由意大利医生兼哲学家 Aloysius Lilius 对儒略历加以改革而制成的一种历法——《格里历》。1582年，时任罗马教皇的格列高利十三世予以批准颁行。

格里历即为现行的公历，日期包括年、月、日。格里历 + UTC 即为日常的日期时间的定义。

3.3. 儒略记日法（Julian Day）

Julian Day，儒略记日法是在儒略周期内以连续的日数计算时间的计时法，是一种不用年月的长期记日法。由 Joseph Justus Scaliger 发明，为了将所有历史日期用一个系统表述，天文学家经常用JD来赋予每天一个唯一的数字，方便追朔日期。

https://en.wikipedia.org/wiki/Julian_day Julian day is the continuous count of days since the beginning of the Julian Period and is used primarily by astronomers, and in software for easily calculating elapsed days between two events (e.g. food production date and sell by date).[1]

3.4. 儒略日数（JDN）

Julian Day Number，指从UT1时正午开始的一整天，是一个整数。

https://en.wikipedia.org/wiki/Julian_day The Julian Day Number (JDN) is the integer assigned to a whole solar day in the Julian day count starting from noon Universal time, with Julian day number 0 assigned to the day starting at noon on Monday, January 1, 4713 BC, proleptic Julian calendar (November 24, 4714 BC, in the proleptic Gregorian calendar),[2][3][4] a date at which three multi-year cycles started (which are: Indiction, Solar, and Lunar cycles) and which preceded any dates in recorded history.[5] For example, the Julian day number for the day starting at 12:00 UT on January 1, 2000, was 2 451 545.[6]

JDN0 指定为：

格里历4714BC的11月24日UT1时12:00:00开始的24小时

或

儒略历4713BC的1月1日UT1时12:00:00开始的24小时。

例如，格里历2000年1月1日UT1时12:00:00开始的JDN是2451545。

3.5. 儒略日（JD）

Julian Date，JD 等于 JDN 加上从 UT1 时 12 时起的小数日部分。

2013年1月1日UT1时00:30:00.000，JD = 2456293.520833

2020年3月30日UTC时01:35:00.000，JD = 2458937.62847

= 2020年3月30日UT1时01:35:00.100

历史上，儒略日基于 $\rm GMT$ 来记录，自1997来，IAU建议以 $\rm TT$ 为单位记录JD。Seidelmann 指出儒略日期可以与国际原子时（$\rm TAI$）、地球时间（$\rm TT$）、协调质心时间（$\rm TCB$）、协调世界时（$\rm UTC$）一起使用，当差异显著时，应指示刻度。通过将中午后的小时、分钟和秒数转换为等效的小数部分，可以找到一天中的小数部分。

https://en.wikipedia.org/wiki/Julian_day The Julian date (JD) of any instant is the Julian day number plus the fraction of a day since the preceding noon in Universal Time. Julian dates are expressed as a Julian day number with a decimal fraction added.[7] For example, the Julian Date for 00:30:00.0 UT January 1, 2013, is 2 456 293.520 833.[8] Current value is as of 01:35, Monday, March 30, 2020 (UTC)

Historically, Julian dates were recorded relative to Greenwich Mean Time (GMT) (later, Ephemeris Time), but since 1997 the International Astronomical Union has recommended that Julian dates be specified in Terrestrial Time.[12] Seidelmann indicates that Julian dates may be used with International Atomic Time (TAI), Terrestrial Time (TT), Barycentric Coordinate Time ( $\rm TCB$ ), or Coordinated Universal Time (UTC) and that the scale should be indicated when the difference is significant.[13] The fraction of the day is found by converting the number of hours, minutes, and seconds after noon into the equivalent decimal fraction. Time intervals calculated from differences of Julian Dates specified in non-uniform time scales, such as UTC, may need to be corrected for changes in time scales (e.g. leap seconds).[7]

3.6. 简化的儒略日

由于儒略日的整数部分过长，为了便于使用，1957年史密松天体物理天文台，将儒略日进行了简化，并将其命名为简化儒略日，其定义为：MJD=JD-2400000.5。

JD2400000是1858年11月16日中午12时，因为JD从中午开始计算，所以简化儒略日的定义中引入偏移量0.5，这意味着MJD0相当于1858年11月17日0时。每一个简化儒略日都在世界时午夜开始和结束。

简化儒略日有两个目的：

1) 日期从午夜而不是中午开始； 2) 儒略日的整数部分由7位数减为5位数，节省计算机储存空间。

3.7. 标准历元（J2000.0）

标准历元（J2000.0）是天文学上使用的历元，前缀J表示是一个儒略纪元。1994年IAU决议明确了新的标准历元为

  2000年1月1日 TT时  12:00:00
= 2000年1月1日 TAI时 11:59:27.816
= 2000年1月1日 UTC时 11:58:55.816

记为 J2000.0。

3.8. 由格里历计算儒略日JD

首先根据日期时间得到年 $Y$，月 $M$，日 $D$ 然后调整 $Y$ 和 $M$

\[\begin{aligned} \left\{\begin{matrix} &M = M+2, Y = Y - 1&\quad(M<3)\\ &M = M, Y = Y&\quad(M\geq3) \end{matrix}\right. \end{aligned}\]

换句话说，如果日期在 1 月或者 2 月，则被看作时前一年的 13 月或 14 月。然后计算辅助系数 $A$ 和 $B$

\[\begin{aligned} A &= floor(Y/100)\\ B &= 2-A+floor(A/4) \end{aligned}\]

然后计算 JD

\[JD=floor(365.25\times (Y+4716))+floor(30.6001\times(M+1))+D+B-1524.5\]

计时间为时 $H$，分 $N$，秒 $S$，毫秒 $MS$，微秒 $US$，将其转换为天为单位，叠加到 JD

\[JD = JD + H/24 + N / 1440 + S/86400 + MS / 86400000 + US / 86400000000\]

特别地，J2000.0 被定义为2000年1月1.5日（TT时），则J2000.0 的儒略日为

\[JD_{J2000.0} = 2451545.0\quad TT\]

由于儒略日JD是一个整数部分和小数部分均很长的double，按照本节直接计算得到的JD，其小数部分的有效位数会被整数部分挤占而不足15位，这在儒略日转为格里历日期时间时会出现精度损失，导致时间中的毫秒和微秒数据不对。

因此，不建议直接采用本节的计算方法计算JD，而是采用类似IAU的sofa程序包的方法，计算简化的儒略日MJD，并在计算过程中分别计算整数部分和小数部分。

同时，建议将儒略日的定义，从原先的一个double变为一个struct，struct包含两个double即整数部分double和小数部分double。相应的修改所有以JD作为形参的函数。

若需要完整的JD，则将整数部分和小数部分相加即可。

3.9. 由格里历算简化的儒略日

参考 sofa 程序 iauCal2jd.c 。

3.10. 计算标准历元起的儒略日

计算当前时刻的 JD_Current_UTC

将其转化为 TT 时

JD_Current_TT = JD_Current_UTC + 64.184 / 86400.0

计算 J2000.0 时刻的 JD_J2000_TT（因为 J2000.0 本身就定义在TT下）

作差，得到 JD_FromJ2000

JD_FromJ2000 = JD_Current_TT – JD_J2000_TT

3.11. 计算标准历元起的儒略世纪

JulianCentry = JDFromJ2000 / 365.25 / 100

其中365.25是儒略年。

4. 参考文献

无。

天文学基础（时间和历法）