本文介绍了 JPL (美国喷气实验室)的星历(DE405)的基本概念,数据组织方式,以及具体的行星数据查询方法。
1. JPL星历
1.1. 概念
JPL planetary ephemerides are generally created to support spacecraft missions to the planets. Selected ephemerides are recommended for more general use.
JPL星历表给出了太阳、月球和九大行星过去和将来的位置信息,并且是开放可使用的。JPL星历表在20世纪60年代由喷气推进实验室建立,最初用作行星探测导航的目的,随着观测技术的不断提高,新的观测数据不断获得,JPL星历表仍在不断修正和完善。 JPL星历表是对描述太阳系动力学系统的微分方程组进行数值积分的结果,因此它的建立基于两个假设:1.微分方程组精确代表了已知的动力学定律,至少在目前观测精度下是如此;2.数值积分程序精度足够高。在这两个假设的前提下,可以构建一个动力学系统,它与太阳系动力学系统是否一致还需要看初始条件和参数是否一致,初始条件和参数通过观测数据来进行最小二乘拟和。观测数据包括:行星探测飞船的测距数据、雷达行星测距数据、月球激光测距、光学观测的测角数据和一些最新的测量手段。 JPL星历表为了精确的表示长时间范围内的天体位置,把长时间范围(数百年)分成短的时间区间(数天),对于每个短的时间区间,它提供一组切比雪夫插值系数,要计算某一时刻的天体位置,首先找到这个短的时间区间,得到切比雪夫插值系数,然后根据切比雪夫插值公式计算天体位置。
1.2. 版本
The latest JPL ephemeris with fully consistent treatment of planetary and lunar laser ranging data is DE430 (Folkner et al 2014). The dynamical model for DE430 includes a frictional damping between the fluid core and the elastic mantle. This damping term is not suitable for extrapolation more than several centuries into the past. In order to cover a longer time span, the ephmeris DE431 was integrated without the lunar core/mantle damping term. The positions of the planets for DE431 agree with the positions on DE430 to within one meter over the time covered by DE430. For the Moon DE431 differs from DE430 mainly in the estimated tidal damping term causing a difference in along-track position of the Moon of 20 meters 100 years from the present and growing quadratically for times more thna 100 years from present.
1.3. 算法
The JPL planetary ephemerides are saved as files of Chebyshev polynomials fit to the Cartesian positions and velocities of the planets, Sun, and Moon, typically in 32-day intervals. The positions are integrated in astronomical units (au), but with polynomials stored in units of kilometers. The integration time units are days of barycentric dynamical time (TDB). Prior to DE430, the value of the astronomical unit was estimated from measurements of planetary orbits using the Gaussian gravitational constant k. Starting with DE430, the astronomical units has been fixed to the value 149597870.700 km as adopted by the International Astronomical Union in 2012.
《高健. 日月、行星位置计算》:JPL-DE405给出的是瞬时日月和行星在ICRS下的位置和速度
http://en.wikipedia.org/wiki/Jet_Propulsion_Laboratory_Development_Ephemeris
DE405 was released in 1998. It added several years’ extra data from telescopic, radar, spacecraft, and VLBI observations (of the Galileo spacecraft at Jupiter, in particular). The method of modeling the asteroids’ perturbations was improved, although the same number of asteroids were modeled. The ephemeris was more accurately oriented onto the ICRF. DE405 covered 1600 to 2200 to full precision.
2. 行星位置计算
2.1. 基本概念
已知某一瞬时时刻(格里历日期+UTC时刻)
转换成儒略日(儒略纪元)
输入 JPL-DE405,得到 ICRS (BCRS)下的太阳、月球、各大行星的位置和速度
然后转至 ITRS 或 J2000 下。
两个关键点:
- JPL查表计算
- ICRS到ITRS或J2000的坐标变换。
2.2. DE405的结构
根据创建时间不同 JPL 星历表有多个版本,这里采用 DE405,它是 1997 年创建的,包括从 1599 年到 2201 年太阳系九大行星和月球的位置。DE405 的文件包括头文件 header.405 和系数文件 ascp****.405 ,**** 代表系数文件的起始时间,每个系数文件包含 20 年天体位置切比雪夫插值系数,例如从 2000 年到 2020 年的系数包含在文件 ascp2000.405 里。
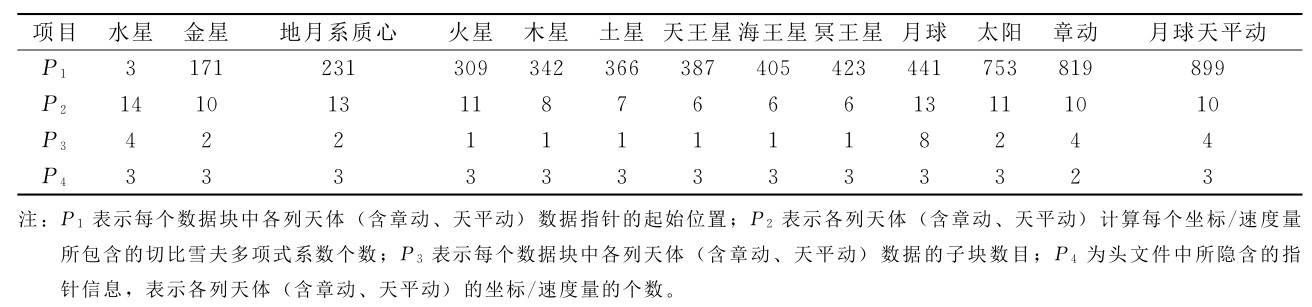
DE405 的头文件 header.405 包含了 DE405 的数据信息、天文常数和数据索引。数据索引是一个 3 行 13 列的表,每列数据代表一个天体的位置数据在数据块内的位置,依次为水星、金星、地月系统、火星、木星、土星、天王星、海王星、冥王星、月球、太阳,第12列数据代表章动角(nutations),包含两个角度:黄经章动 $\Psi$ 和交角章动 $\epsilon$ ,第13列数据代表岁差参数,包含三个欧拉角:$\zeta, z, \theta$ 。每列的第一行指示该天体数据在数据块的起始位置,第二行表示切比雪夫多项式的阶数,第三行表示该天体的数据被划分成几个子区间。下表展示的 DE421 与 DE405 的数据结构相同,最后一列是数据的维度( 3 表示三轴)。
例如水星的数据索引为3、14、4,其中:
- 数字 3 表示水星的数据从数据块内第 3 个数据开始,
- 数字 14 为切比雪夫多项式阶数,即每轴位置用 14 个切比雪夫系数表示,共有 $x$、$y$、$z$ 三轴的系数,
- 数字 4 为划分的子区间个数,由于星体运动周期不同,划分的子区间个数也不一样,周期较短,运动不规则的星体子区间个数较多(其中月球最多为8个子区间),同样的时间内表示位置的数据量也大
水星在 32 天内表示位置的数据个数为 $14\times 4\times 3=168$ 个,等式中的 3 代表三个轴。
系数文件 ascp2000.405 则由若干个数据块组成,每个数据块为 32 天的数据。DE405 的数据信息包括起始时间、结束时间、数据块的个数、每个数据块的数据个数、数据块的时间长度;天文常数包括光速、天文单位、地月质量比等;数据索引用来指示某一天体的数据在数据块内的位置。系数文件 ascp2000.405 由 229 个数据块组成,每个数据块代表 32 天,包含 1018 个数据。每个数据块第一行是标号和数据个数,从第二行开始,每三个数据一行,第一个数据是数据块起始时间,第二个数据是数据块终止时间,然后依次是水星、金星等的位置数据和章动、岁差数据。
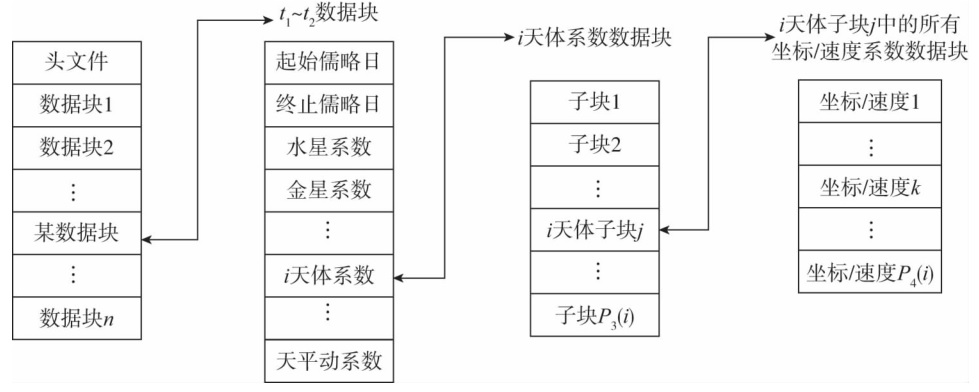
一个完整的DE星历表结构如下图所示。
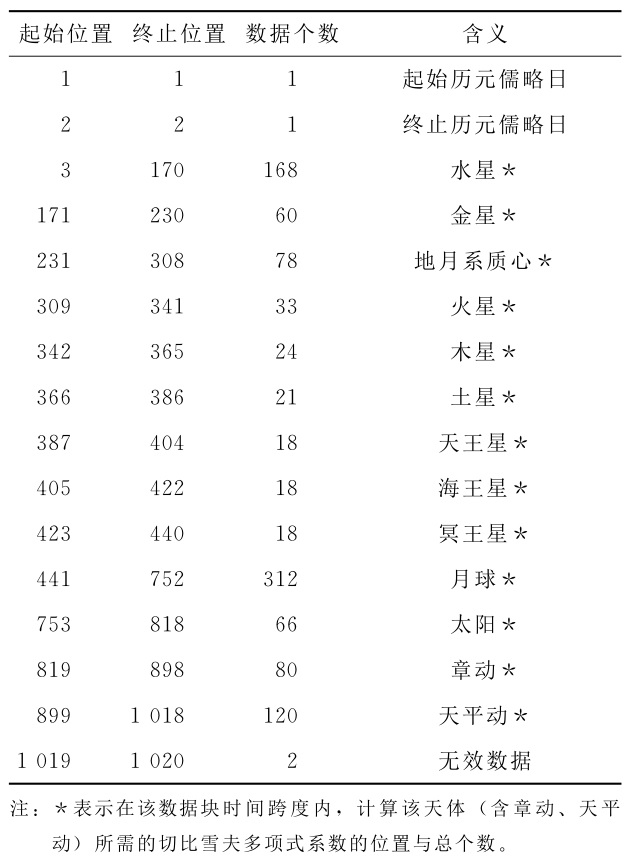
某个数据块内的数据如下表所示。
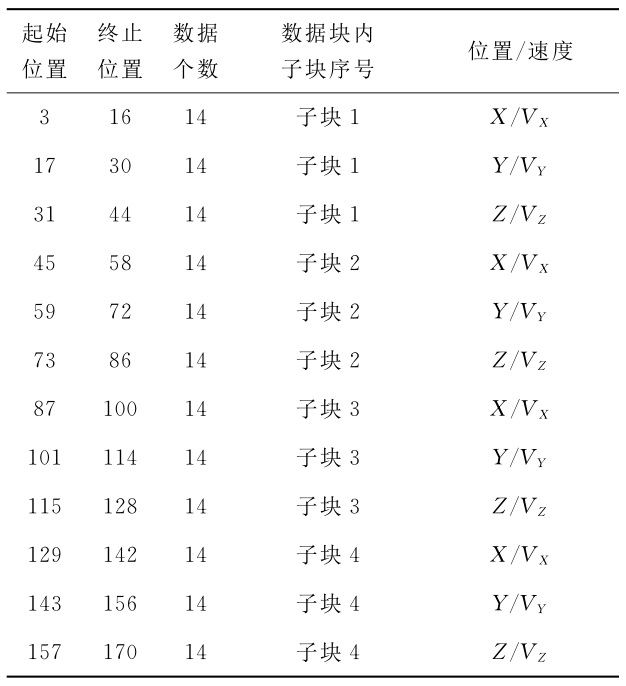
某个数据块内水星子块的时间跨度如下表所示。
某数据块内水星子块的各个数据的含义如下表所示。
2.3. DE405的计算
JPL 星历采用儒略日形式的 TDB 时刻作为插值时刻,双精度数,可用 TT 代替,精度损失可忽略。JPL 星历采用 ICRS 参考系?
DE405采用的坐标系是以太阳系质心为原点,J2000地球平赤道面为 $xy$ 平面, J2000 平春分点方向为 $x$ 方向的直角坐标系。插值得到的位置坐标是在这个坐标系下的值(除月球外,月球坐标以地心为原点)。
要得到其它坐标系下天体位置的表示,需要进行坐标的平移和旋转变化,在轨道动力学中使用的惯性坐标系一般以地球质心为原点,J2000 地球平赤道为 $xy$ 面和平春分点方向为 $x$ 方向,从 DE405 的坐标转换到地心惯性坐标系,只需要进行坐标平移。DE405的时间单位为日,$1 day = 86400 s(SI)$,距离单位为 km,速度单位为 km/day。
2.4. 地球太阳矢量计算
由于 JPL 星历只给出了地月系统的坐标和月球的坐标,需要通过几何方式算出地球的位置坐标。
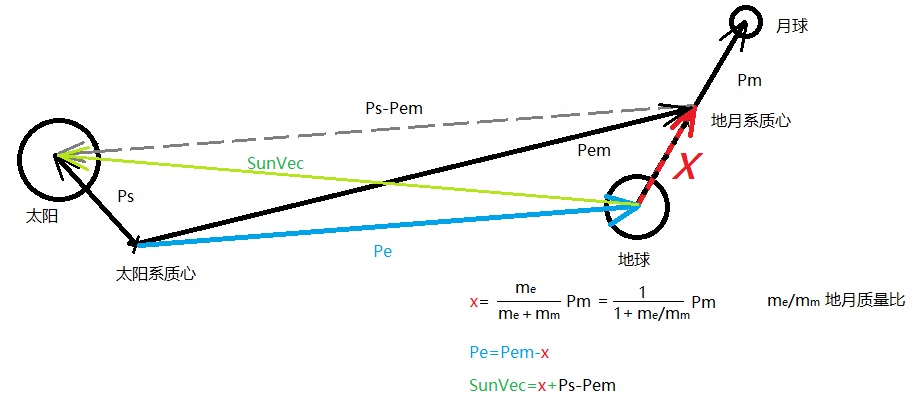
祭出不忍直视的草图。如图所示,假设 $x$ 为地球质心指向地月系质心(地月系统质心)的矢量,$m_e,m_m$ 分别为地球和月球质量,$P_m$ 为以地球中心为原点的月球坐标(星历查询可得),那么有 \(x=\frac{m_m}{m_m+m_e}P_m=\frac{1}{1+\frac{m_e}{m_m}}P_m\) 其中,$m_e/m_m=0.813005600000000044\times 10^2$ 是地月质量比。
那么,地球矢量 $P_e=P_{em}-x$,以地球为中心的太阳矢量 $SunVec=x+P_s-P_{em}$。其中,$P_s$ 为星历查询得到的太阳位置矢量。
3. 参考文献
[1] 高健. 《日月、行星位置计算》.
[2] Wikipedia. JPL Ephemeris.