人工智能（知识表示、推理与知识图谱）

卷积神经网络是一种专门用于处理网格状数据（如图像、视频）的深度学习模型，其核心思想是通过局部感受野、权值共享和层次化特征提取来自动学习数据的空间或时序模式。

• 1. 知识的基本概念
  • 1.1. 什么是知识
  • 1.2. 知识的分类
• 2. 知识表示
  • 2.1. 基于符号逻辑的表示
    • 2.1.1. 一阶谓词逻辑表示法
      • 2.1.1.1. 命题逻辑
      • 2.1.1.2. 个体与谓词
      • 2.1.1.3. 一阶谓词
      • 2.1.1.4. 连接词与量词
      • 2.1.1.5. 论域与特征谓词
      • 2.1.1.6. 推理规则
      • 2.1.1.7. 归结原理
    • 2.1.2. 产生式表示法
      • 2.1.2.1. 基本形式
      • 2.1.2.2. 推理方法
    • 2.1.3. 框架式表示法
      • 2.1.3.1. 框架的定义
      • 2.1.3.2. 层次与继承
      • 2.1.3.3. 示例
    • 2.1.4. 对比与总结
  • 2.2. 基于RDF的表示
    • 2.2.1. RDF
    • 2.2.2. RDF 的序列化
    • 2.2.3. RDF-Schema
    • 2.2.4. OWL
  • 2.3. 基于嵌入的表示
• 3. 知识推理
• 4. 知识图谱
• 5. 参考文献

---

1. 知识的基本概念

1.1. 什么是知识

• 知识是人们在长期的生活及社会实践中、在科学研究及实验中积累起来的对客观世界的认识与经验
• 人们把实践中获得的信息关联在一起，就形成了知识

知识与人工智能的关系：

• 知识是智能的基础，为了使计算机具有智能，能够模拟人类的智能行为，就必须使它具有知识
• 人类的知识需要用适当的形式表示出来，才能存储到计算机中并被运用

1.2. 知识的分类

知识可以从不同的维度进行分类，以下是两种典型的分类情况：

• 规则性知识与事实性知识

  规则性知识反映了信息间的某种因果关系，可以用 “如果……则……” 的形式来表示

  例：“如果动物是鸟，则该动物是卵生生物”

  事实性知识反映了事物的某些性质

  例例：“篮球是圆的”，“水是透明的”

• 确定性知识与不确定知识

  确定性知识：表示确定的规则或事实

  例例：“如果这个粒子为电子，则这个粒子一定带负电”

  不确定性知识：事物与事物间的规则与联系是不确定和模糊的

  例例：“如果今天阴天，则明天可能会下雨”

思考：能否列举一个「不确定的事实性」知识？

• “橡皮擦可能是圆的”
• “如果我理发，则我可能变帅”

2. 知识表示

知识表示（Knowledge Representation）是指将知识以一种机器可理解的形式表示出来，它涉及数据结构及其处理机制的综合：

表示= 数据结构+处理机制

在知识表示中，知识的涵义与日常生活中的知识有所不同，它是指以某种结构化的方式表示的概念、事件和过程。

知识表示技术的变化大致可以分为三个阶段：

1. 基于符号逻辑的表示：主要包括逻辑表示法（如一阶逻辑、描述逻辑）、产生式表示法和框架表示等。逻辑表示与人类的自然语言比较接近，是最早使用的一种知识表示方法。

2. 基于RDF的表示：随着语义网概念的提出，万维网内容的知识表示技术逐渐兴起，基于万维网研发了资源语义元数据描述框架（Resource Description Framework，RDF），提供了一个用于描述实体/资源的统一标准。由于 RDF 只是定义了一个标准，需要采用基于标签的半结构置标语言XML（又被称为可扩展标记语言，eXtensible Markup Language）做为描述这种抽象的数据模型的具体书写方式，被称为 RDF/XML。

3. 基于嵌入的表示：随着自然语言处理领域词向量等嵌入(Embedding)技术手段的出现，采用连续向量方式来表示知识的研究（TransE 翻译模型、SME、SLMNTN、MLP，以及NAM神经网络模型等）正在逐渐取代与上述以符号逻辑为基础知识表示方法相融合，成为现阶段知识表示的研究热点。更为重要的是，知识图谱嵌入也通常作为一种类型的先验知识辅助输入到很多深度神经网络模型中，用来约束和监督神经网络的训练过程。

2.1. 基于符号逻辑的表示

2.1.1. 一阶谓词逻辑表示法

一阶谓词逻辑表示法（First-Order Predicate Logic, FOPL）是一种重要的知识表示方法，以数理逻辑为基础，是能够表达人类思维活动规律的一种精准的形式语言。一阶谓词逻辑表示法与人类的自然语言比较接近，可以被方便地输入到计算机中进行存储和运算。

2.1.1.1. 命题逻辑

在命题逻辑中，命题是一个非真即假的陈述句。一个命题不可以同时为真又为假，但是可以在一种条件下为真，另一种条件下假。命题逻辑表示有较大的局限性：

• 无法把它所描述的事物的结构即逻辑特征反映出来。 如 “老李是小李的父亲” 用命题逻辑就是一个字母 $y$，看不到内部的逻辑结构。
• 无法把两者共同的特征表示出来。如 “李白是诗人” 和 “杜甫是诗人” 用命题逻辑就是两个字母 $p$, $q$ 。

由于这些原因，在命题逻辑的基础上发展起来了谓词逻辑，谓词逻辑具体组成包括谓词和个体两个部分。

2.1.1.2. 个体与谓词

（原子）命题本身是对一个事物性质的直接描述，或是对几个事物之间关系的判断。这里的 “事物” 就被称为个体。个体通常可以替换为其他的实例，这种不确定性使得个体具有 “变量” 的意味，我们以小写字母 $x,y,z,\cdots$ 来表示个体，称为 个体变量。

对个体进行性质或关系的判断，称为谓词。谓词是从个体变量到真值的映射，使之具有 “函数” 的意味。我们通常使用大写字母 $P,Q,R,\cdots$ 表示一个谓词，并在其后的括号中填入个体变量表示对其判断。例如 $\text{P}(x)$ 表示 “$x$ 具有性质 $\text{P}$”。

谓词的一般形式是：

\[\text{P}(x_1,x_2,x_3,\cdots,x_n)\]

其中 $P$ 是谓词，用来刻画个体的性质，状态和个体间的关系。个体 $x_1, \cdots, x_n$ 表示独立存在的事物或者某个抽象的概念。

2.1.1.3. 一阶谓词

如果个体是常量，变量或函数，称之为一阶谓词。

• 个体可以是常量：例如 “老张是教师” 可以用谓词逻辑表示为：

  \[\text{Teacher}(zhang)\]

  $\text{Teacher}$ 这个谓词名刻画了 $zhang$ 这个个体是教师这一性质。

• 个体可以是变量：例如 $x<5$ 可以用谓词逻辑表示为：

  \[\text{Less}(x,5)\]

  less这个谓词名刻画了个体 $x$ 比个体 $5$ 小这一关系。当 $x$ 有具体的值的时候，这个谓词就有了具体的真 $T$ 或假 $F$ 的判定。同时，个体也存在个体域的概念，也即个体变量的取值范围。

• 个体可以是函数：例如 “小李的父亲是教师” 可以用谓词逻辑表示为：

  \[\text{Teacher}(\text{Father}(li))\]

  $\text{Father}(li)$ 是一个函数。谓词名 $\text{Teacher}$ 刻画了这个函数值 $\text{Father}(li)$ 的职业是教师这一性质。

相比于命题逻辑，一阶谓词逻辑的优势如下：

• 一个事实性陈述：“A是B的老师”，命题逻辑只能将其定义为一个 $p$，而一阶谓词逻辑可以刻画其中的关系：

\[\text{Teacher}(A,B)\]

• 可以构建二元谓词表示更加复杂的逻辑，如 “小李的妹妹和小张的哥哥结婚” 可以表示为：

\[\text{Married}(\text{Sister}(li),\text{Brother}(zhang))\]

• 谓词（函数）还可以递归调用，例如 “小李的祖父” 可以表示为：

\[\text{Father}(\text{Father}(li))\]

尝试用一阶谓词逻辑描述如下命题 Smith 作为一个工程师为 IBM 工作

\[\text{Work}(\text{Engineer}(Smith), IBM)\]

2.1.1.4. 连接词与量词

为了形成更为复杂的知识，需要额外定义两个概念，连接词 与 量词：

• 连接词：
  • 否定（非）：$\lnot$ 析取（或）：$\lor$ 合取（且）：$\land$ 蕴含（推出）：$P\to Q$，$P$ 为前件，$Q$ 为后件 等价（当且仅当）：$P\leftrightarrow Q$，$P$ 当且仅当 $Q$
• 量词：
  • 全称量词（任意）：$\forall$
  • 存在量词（存在）：$\exist$

量词是区分命题逻辑和一阶谓词逻辑的关键概念：

• 命题逻辑：

  • 人都会死 $p$，苏格拉底是人 $q$，苏格拉底会死 $r$：$(p\land q)\rightarrow r$
  • 人都会死 $p$，小明是人 $s$，小明会死 $t$：$(p\land s)\rightarrow t$
  • 无法归纳出其中的共性。

• 一阶谓词逻辑：

  思考：如何表述？

  • 人都会死：$\forall x\;\text{People}(x)\rightarrow \text{Die}(x)$
  • 归纳给共性并形成逻辑特征：
  • 人都会死，苏格拉底是人，苏格拉底会死：$\text{People}(S)\rightarrow \text{Die}(S)$
  • 人都会死，小明是人，小明会死：$\text{People}(M)\rightarrow \text{Die}(M)$

全称量词和存在量词出现的次序会影响命题的意思：

尝试解读如下两个命题： - （1）$\forall x\; \exist y\;(\text{Student}(x)\to \text{Teacher}(y,x))$ - （2）$\exist y \;\forall x\; (\text{Student}(x)\to \text{Teacher}(y,x))$

• （1）每个学生都有一个老师
• （2）有一个人是所有学生的老师

2.1.1.5. 论域与特征谓词

注意以下两个例子：

• （1）规则知识：“如果动物是鸟，则动物是卵生生物”
• （2）事实知识：“鸟是卵生动物”

虽然二者很相似，但在知识表示中完全不同。一个朴素的例子为：

graph TD
A[“麻雀是鸟”（事实知识）] --> B{（1）“动物是鸟”？}
C[“麻雀是动物”（事实知识）] --> B
    B -->|是| D[“麻雀是卵生生物”]

F[“麻雀是鸟”（事实知识）] --> G[“麻雀是卵生生物”]
H[（2）“鸟是卵生生物”（事实知识）] --> G

可以看出，类似的知识，可能按照不同的方式进行表示。

采用一阶谓词逻辑，“鸟是卵生动物” 可表示为：

\[\forall bird\; \text{From}(bird, egg)\]

或者表示为：

\[\forall x\; \text{From}(x, egg)\]

此时需要限定个体变量 $x$ 存在的范围（此例中为鸟类），称其为 论域（类似变量的定义域）。

如果扩大论域，显然可能会导致命题失效，比如将 $x$ 扩大为动物，此时为了保证原命题成立，需要额外引入一个谓词，以限定论域的范围，这个额外引入的谓词被称为 特征谓词。此时有

\[\forall x\; (\text{Bird}(x)\to \text{From}(x, egg))\]

2.1.1.6. 推理规则

基于前述一阶谓词逻辑的定义，我们想要对命题进行推理，一边确定命题的真假。推理需要一定的规则，在特定假设下能获得特定结论。

假设有公式 $\phi_1, \phi_2,\cdots, \phi_n$ 被称为 前提，和另外一个公式 $\psi$ 被称为 结论，我们希望在使用一系列证明规则后，通过假设能得到结果

\[\phi_1, \phi_2,\cdots, \phi_n \vdash \psi\]

上式被称为相继式（sequence），如果可以建立证明，就称他为有效的（valid）。符号 $\vdash$ 是句法后承（syntactic consequence）关系。上式读作 “$\psi$ 可证明自 $\phi_1, \phi_2,\cdots, \phi_n$”。

一阶谓词逻辑的推理论证与命题逻辑类似，一共包含以下九个 基本推理规则：

• 合取规则

  • 合取引入（and-introduction）

    \[\frac{P \quad Q}{P\land Q}\]

  • 合取除去（and-elimination）

    \[\frac{A \land B}{A}\quad \frac{A \land B}{B}\]
    尝试证明： \(P\land Q, R \vdash Q \land R\)

    证明：

    \[\frac{\frac{P \land Q}{Q}\quad R}{Q\land R}\]

• 双重否定

  \[\frac{\lnot \lnot P}{P} \quad \frac{P}{\lnot \lnot P}\]
  尝试证明： \(P, \lnot \lnot (P\land Q) \vdash \lnot \lnot P\land Q\)

  证明：

  \[\frac{\frac{P}{\lnot \lnot P}\quad \frac{\frac{\lnot \lnot (P\land Q)}{P\land Q}}{Q} }{\lnot \lnot P\land Q}\]

• 蕴含消去

  • 肯定前件（分离规则） \(\frac{P\to Q, P}{Q}\)

  • 否定后件（反证规则，拒取式） \(\frac{P\to Q, \lnot Q}{\lnot P}\)

    思考：下面的命题是否成立？ \(\frac{P\to Q, \lnot P}{\lnot Q}\)

    不成立。比如，“如果下雨地一定湿”

    否定后件表述为：如果地没湿则一定没下雨（为真）

    但上述表述为：如果没下雨则地一定没湿（不一定）

• 假言推导（蕴含引入）

  \[\frac{\begin{bmatrix} P\\ \vdots\\ Q \end{bmatrix}}{P\to Q}\]
  • 也就是说，为了证明 $P\to Q$，先短暂假设 $P$ 成立，再证明 $Q$，这个假设在框外不再成立。

  • 紧跟在关闭矩形框后的行必须与使用该矩形框的规则所得到的结论 模式匹配，就蕴含引入而言，如果矩形框第一个公式是 $P$，最后一个公式是 $Q$，那么该矩形框后面的行必须是 $P \to Q$。

    尝试用假言推导证明如下经典命题： \(P\to Q \vdash \lnot Q \to \lnot P\)

    证明：

    \[\frac{\begin{bmatrix} \frac{P\to Q \quad \lnot Q}{\lnot P} \end{bmatrix}}{\lnot Q \to \lnot P}\]

• 析取规则

  • 析取引入

    \[\frac{P}{P\lor Q} \quad \frac{Q}{P\lor Q}\]

  • 析取消除

    \[\frac{P\lor Q\quad\begin{bmatrix} P\\ \vdots\\ A \end{bmatrix} \quad \begin{bmatrix} Q\\ \vdots\\ A\end{bmatrix}} {A}\]

  • 对于析取消除，由于不知道 $P, Q$ 哪一个为真，必须给出两个单独的证明，在合成一个论断。

由于量词的引入，一阶谓词逻辑的推理还有四个额外推理规则：

• 全称量词消除（Universal Specification, US）：

  \[\forall x\; P(x) \Rightarrow P(c)\]
  • $c$ 为个体域中任一确定元素
  • 前提：所有人都会死 $\forall x\; (\text{People}(x)\to \text{Die}(x))$
  • 结论：苏格拉底会死 $\text{People}(Socrates)\to \text{Die}(Socrates)$

• 全称量词引入（Universal Generalization, UG）：

  \[P(c) \Rightarrow \forall x\; P(x)\]
  • $c$ 为个体域中任一确定元素
  • 如果在推理过程中，对于个体变量 $c$ 的一个任意但固定的选择（$c$ 不在前提中的任何公式中自由出现），我们证明了命题 $A(c)$ 为真，那么我们可以合法地在推理的下一步引入全称量词，得到 $\forall x\; P(x)$。
  • 一个我们很熟悉的例子，那就是“毕达哥拉斯定理”。随手在纸上画一个“直角三角形”，证明直角边的平方和，等于斜边的平方。就可以推广到所有的直角三角形。

• 存在量词消除（Existential Specification, ES）：

  \[\exist x\; P(x) \to P(c)\]
  • 前提：有一些美国总统来自德州
  • 结论：某个美国总统来自德州
  • 需要注意到，这 “某个美国总统”，是有限制的。德州出来的总统总共只有那么几个，那么 “某个美国总统” 可以肯定就是他们当中的一个。

• 存在量词引入（Existential Generalization, EG）：

  \[P(c) \to \exist x\; P(x)\]
  • 爱因斯坦是天才 $\to$ 存在天才：$\text{Genius}(Einstein)\to \exist x\;\text{Genius}(x)$

详细参考《离散数学》

尝试证明： \(\forall x\forall y (P(x,y)\to W(x,y)), \; \lnot W(a,b)\quad \vdash \quad \lnot P(a,b)\)

证明：

(1) $\forall x\forall y (P(x,y)\to W(x,y))\quad$ [前提]

(2) $\forall y (P(a,y)\to W(a,y))\quad$ [(1),US]

(3) $P(a,b) \to W(a,b)\quad$ [(2), US]

(4) $\lnot W(a,b)\quad$ [前提]

(5) $\lnot P(a,b)\quad$ [(4),拒取式]

尝试证明： 前提：$\exist x\;(\text{Cat}(x)\land \text{Catch}(x,rat))$，证明：存在抓老鼠的动物

证明：

(1) $\exist x\;(\text{Cat}(x)\land \text{Catch}(x,rat))\quad$ [前提]

(2) $\text{Cat}(c)\land \text{Catch}(c,rat)\quad$ [(1),ES]

(3) $\text{Catch}(c,rat)\quad$ [合取除去]

(4) $\exist y \;\text{Cat}(y,rat)\quad$ [(3),EG]

2.1.1.7. 归结原理

归结演绎推理是基于一种称为归结原理（亦称消解原理，Resolution Principle）的推理规则的推理方法。归结原理是由鲁滨逊*（J.A.Robinson）于 1965 年首先提出。其核心是通过归结操作推导空子句以验证命题的不可满足性，它是谓词逻辑中一个相当有效的机械化推理方法。归结原理的出现，被认为是自动推理，特别是定理机器证明领域的重大突破。

给定以下知识库（CNF 形式）：

(1) $\lnot P(x) \lor Q(f(x))$ （如果 $P(x)$ 成立，则 $Q(f(x))$ 成立）

(2) $\lnot Q(y) \lor R(g(y))$ （如果 $Q(y)$ 成立，则 $R(g(y))$ 成立）

(3) $P(a)$ （$P(a)$ 为真）

需要证明：

(4) $\lnot R(z)$ （ $R(z)$ 不成立，即目标子句）

• 步骤 1：归结子句 (1) 和 (3)

  • 子句 1: $\lnot P(x) \lor Q(f(x))$

  • 子句 3: $P(a)$

  • 互补文字：$\lnot P(x)$ 和 $P(a)$，通过合一 ${x/a}$ 消解

  • 归结式：$Q(f(a))$（新子句 5）

  当前子句集：

  • (1) $\lnot P(x) \lor Q(f(x))$

  • (2) $\lnot Q(y) \lor R(g(y))$

  • (3) $P(a)$

  • (4) $\lnot R(z)$

  • (5) $Q(f(a))$

• 步骤 2：归结子句 (5) 和 (2)

  • 子句 5: $Q(f(a))$

  • 子句 2: $\lnot Q(y) \lor R(g(y))$

  • 互补文字：$Q(f(a))$ 和 $\lnot Q(y)$，通过合一 ${y/f(a)}$ 消解

  • 归结式：$R(g(f(a)))$（新子句 6）

  当前子句集：

  • (1) $\lnot P(x) \lor Q(f(x))$

  • (2) $\lnot Q(y) \lor R(g(y))$

  • (3) $P(a)$

  • (4) $\lnot R(z)$

  • (5) $Q(f(a))$

  • (6) $R(g(f(a)))$

• 步骤 3：归结子句 (6) 和 (4)

  • 子句 6: $R(g(f(a)))$

  • 子句 4: $\lnot R(z)$

  • 互补文字：$R(g(f(a)))$ 和 $\lnot R(z)$，通过合一 ${z/g(f(a))}$ 消解

  • 归结式：$\square$（空子句，矛盾）

由于导出了空子句 $\square$，说明原子句集是矛盾的，即 $R(z)$ 与知识库无法同时成立。

2.1.2. 产生式表示法

产生式表示法，也称为规则表示法，由美国数学家波斯特（E.POST）在1943年首先提出。1972年，纽厄尔和西蒙在研究人类的认知模型中开发了基于规则的产生式系统，产生式表示法已经成了人工智能中应用最多的一种知识表示模式，尤其是在专家系统方面，许多成功的专家系统都是采用产生式知识表示方法。

2.1.2.1. 基本形式

产生式表示法的基本形式是：

IF <前提> THEN <结论/动作></span>

它描述了一个 “条件-行为” 对：如果某个条件成立，那么就执行某个操作或得出某个结论。这个术语来源于形式语言理论中的 “产生式规则”（例如，在巴科斯-诺尔范式 BNF 中，用 $::=$ 来定义语法结构），但在知识表示中，它的含义更接近于逻辑中的“蕴含式”（Implication），即 $P \to Q$。

一个典型的产生式规则由三部分组成：

• 前提（条件部分 / IF 部分）：也称为左部（Left-Hand Side, LHS）。它是一个或一组条件，可以是逻辑组合（与、或、非）。

  例如：(温度 > 38.5℃) AND (咳嗽 == True)

• 结论（动作部分 / THEN部分）：也称为右部（Right-Hand Side, RHS）。当前提被满足时，所执行的操作或所得的结论。

  例如：THEN 诊断为“疑似流感” 或 THEN 开出药物“奥司他韦”

• 可信度（可选）：在不确定推理中，可以为规则附加一个可信度因子（Certainty Factor, CF），表示前提成立时，结论为真的概率或置信程度。

示例：

规则 R1:
IF    动物有毛发
THEN  该动物是哺乳动物   (CF=0.9)

规则 R2:
IF    动物产奶
THEN  该动物是哺乳动物   (CF=1.0)

规则 R3:
IF    动物是哺乳动物 AND 动物有蹄
THEN  该动物是有蹄类动物

2.1.2.2. 推理方法

产生是表示法的推理方法包括：

1. 前向推理（Forward Chaining），也称为 “Horn 规则推理”，或称为数据驱动方式，是一种基于规则的推理方法，它通过将规则的左部作为输入，将规则的右部作为输出，并重复执行此过程，直到所有规则都被执行完毕，或通过规则库求得结论。正向推理会得出一些与目标无直接关系的事实，是有浪费的。
   思考：能否举例说明？

   如，已知病然感染了某疾病，推理出他有什么症状。可能推理出：生病–意识模糊–长期卧床–肌肉萎缩

2. 后向推理（Backward Chaining），也称为“ 逆向规则推理”，或称为目标驱动方式，是一种基于规则的推理方法，它通过将规则的右部作为输入，将规则的左部作为输出，并重复执行此过程，直到所有规则都被执行完毕。如果目标明确，使用反向推理方式效率较高。
   思考：能否举例说明？

   如，已知病人出现发烧、胸闷、气短的现象，推理出病人得了什么病。此时规则库中一般会包含大量某疾病导致某些症状的规则，便于反向推理。

3. 双向推理（Bidirectional Chaining），也称为 “双向规则推理”，是一种基于规则的推理方法，它同时执行前向推理和后向推理，直到所有规则都被执行完毕。

不管是何种推理规则，在执行过程中都会得到不只一条规则被满足，此时推理机需要根据某种策略（如优先级、特异性、新近度等）选择一条规则来执行。

产生式表示格式固定，形式单一，规则（知识单位）间相互较为独立，没有直接关系使知识库的建立较为容易，处理较为简单的问题是可取的。另外推理方式单纯，也没有复杂计算。特别是知识库与推理机是分离的，这种结构给知识的修改带来方便，无须修改程序，对系统的推理路径也容易作出解释。所以，产生式表示知识常作为构造专家系统的第一选择的知识表示方法。

2.1.3. 框架式表示法

框架式表示法是一种基于人类理解和记忆事物方式的知识表示方法，非常擅长描述具有固定结构的典型对象、概念或事件。

框架（Frame） 是由 Marvin Minsky 在 1974 年提出的一种知识表示理论。其核心思想是： 当人们遇到一个新情况时，会从记忆中找到一个被称为“框架”的结构化数据结构。这个框架提供了一个大致的轮廓，人们通过用新情况的细节填充这个框架来理解和应对它。

一个框架就像一张体检表、一份入职申请表或一个产品目录，它预先定义好了需要填写哪些栏目，你只需要根据具体的人或物填入具体信息即可。

2.1.3.1. 框架的定义

一个框架主要由 「框架名」 和一系列 「槽（Slot）」 组成。每个槽又可以包含多个 「侧面（Facet）」 来说明该槽的细节。

• 框架名：标识这个框架所描述的主题或类别。
  • 例如：笔记本电脑、员工、会议室预订事件
• 槽：描述了框架所代表实体的各个属性或组成部分。
  • 例如：对于 笔记本电脑 框架，它的槽可以有：品牌、型号、CPU、内存、硬盘等。
  • 例如：对于 员工 框架，槽可以有：姓名、工号、部门、职位、薪资等。
  • 思考：会议室预订事件可以有哪些槽？

    如，会议时间、房间号（地点）、参会人员等。

• 侧面：是槽的进一步细化，用于描述槽的附加信息。最常见的侧面有：
  • 值（Value）：该属性的具体取值。这是最核心的侧面。
  • 默认值（Default）：当没有明确信息时，该属性的典型值。例如，“鸟”的框架中，“会飞”的默认值可能是“是”，但鸵鸟这个实例会将其覆盖为“否”。
  • 值类型（Type）：规定该槽的取值范围，如数字、字符串、布尔值，甚至是另一个框架。
  • 范围（Range）：规定值的区间，如 1-100。
  • 可选【一段程序（过程附件）】，当需要该槽的值但当前未知时，会自动调用这段程序来计算或获取值（例如，通过询问用户）。
  • 可选【一段程序（后处理）】，当该槽被填入新值后，自动触发执行（例如，更新数据库或其他相关槽的值）。

2.1.3.2. 层次与继承

框架表示法的一个强大特性是它天然支持层次结构（继承）。

• AKO（A-Kind-Of）： 用于表示类与子类的关系（类属关系）。
  • 例如：轿车 框架的 AKO 槽的值是 汽车。这意味着“轿车是一种汽车”，因此轿车框架可以继承 汽车 框架的所有槽（如都有轮子、发动机），并增加自己特有的槽（如轿车车型）。
• ISA（Is-A）： 用于表示 「实例与类」的关系（实例关系）。
  • 例如：一个具体的对象 我的电脑 框架的 ISA 槽的值是 笔记本电脑。这意味着 “我的电脑是一台笔记本电脑”，因此它继承了 笔记本电脑 框架的所有属性，并为各个槽填上了具体的值（如品牌：Dell，型号：XPS 13）。

这种继承机制极大地减少了信息冗余，实现了知识的重用。

2.1.3.3. 示例

假设我们要描述 “一辆具体的汽车”。

• 首先，我们有一个上层框架（类）：

  框架名:  【汽车】 AKO: 交通工具
  轮子数量: 默认值: 4
  发动机:   值类型: 框架
  功能:     行驶
  

• 然后，定义一个更具体的子类框架：

  框架名:  【轿车】 AKO: 【汽车】   
  车型:     值类型: 字符串，范围: [普通, 跑车, 敞篷]
  

• 最后，定义一个具体实例的框架：

  框架名: 【张三的车】 ISA: 【轿车】
  品牌:      值: "Toyota"
  型号:      值: "Camry"
  发动机:    值: 【发动机-编号A123】
  颜色:      值: "黑色"
  购买时间:  值: 2022-03-15
  里程数:    值: 15000
            (fcn): 当里程数更新时，计算是否需要保养
  

• 被引用的框架：

  框架名:    【发动机-编号A123】
  ISA:       【V6发动机】
  排量:      值: 3.5
  马力:      值: 301
  

2.1.4. 对比与总结

与产生式表示法的对比：

特征	产生式表示法	框架表示法
基本单元	规则 (IF-THEN)	框架 (对象-属性)
知识类型	善于表示过程性知识和判断规则	善于表示陈述性知识和静态描述
组织方式	规则集合，相对扁平	层次化的框架网络
核心机制	匹配-触发	属性填充、继承
类比	一本操作手册（告诉你什么情况该做什么）	一张信息登记表（告诉你一个东西由什么组成）

总结：

特性	描述	优点
结构性	知识被组织成结构化的单元， 符合人类对事物的认知习惯。	表达能力强，能清晰地描述复杂对象。
继承性	通过AKO和ISA关系实现属性继承。	减少知识冗余，简化知识库的构建和维护。
自然性	用“对象-属性-值”的方式表示，非常直观。	易于理解和实现。
封装性	将描述一个对象的所有信息 封装在一个框架内。	模块化好，便于管理。
过程性知识结合	通过if-needed、if-added 等侧面附加过程（代码）。	知识表示灵活，具备动态计算和推理能力。

缺点	描述
缺乏形式化基础	不如逻辑表示法那样有严谨的数学基础，推理可能不严格。
构建成本高	构建一个高质量的框架网络需要大量的领域知识和设计工作。
效率问题	在继承链很长时，查找效率可能会降低。

在实际的专家系统中，这两种方法常常结合使用：

• 用框架来表示系统诊断/配置的对象（例如：患者、汽车、计算机组件）。
• 用产生式规则来表示关于这些对象的专家经验和推理知识（例如：IF 汽车无法启动 AND 启动机无声 THEN 检查蓄电池）。规则的前提和结论都可以操作框架中的槽。

2.2. 基于RDF的表示

2.2.1. RDF

RDF（Resource Description Framework，资源描述框架）是一种用于表示信息的标准模型，主要用于描述 网络资源 的语义信息。RDF是万维网联盟定义的标准，用于描述网络资源。其核心思想非常简单却非常强大：

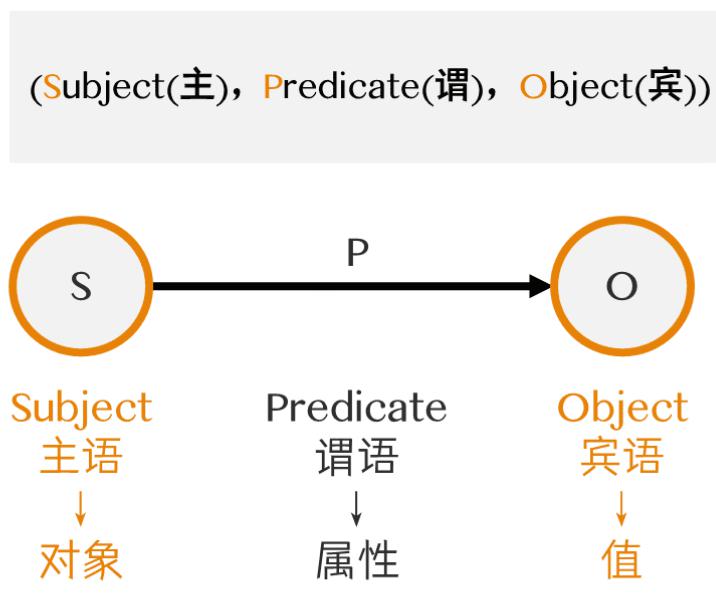
用 “主语-谓语-宾语” 的形式，将世界描述为一个个相互连接的陈述。

上述三元组中：

• 主语（Subject）：你要描述的资源（事物）。例如：http://example.org/Alice

• 谓语（Predicate）：资源的某个属性或它与另一个资源的关系。例如：http://schema.org/knows

• 宾语（Object）：属性的值。这个值可以是一个文字（如字符串、数字），例如：http://example.org/Bob ；也可以是另一个资源，例如：”三体”

上述三元组表达了一个事实：Alice 认识 Bob（或了解《三体》这本书）.

从 RDF 的名称我们不难看出，其是一个描述框架，任何满足其框架规定的描述都可以成为 RDF 描述。为了将 RDF 的描述具体化，我们定义如下：

• 资源（Resource）：所有以 RDF 表示法来描述的东西都叫做资源，它可能是一个网站，可能是一个网页，可能只是网页中的某个部分，甚至是不存在于网络的东西，如纸本文献、器物、人等。在 RDF 中，资源是以统一资源标识（URI，Uniform Resource Indentifiers）来命名，其中：
  • 统一资源定位器（URL，Uniform Resource Locators），
  • 统一资源名称（URN，Uniform Resource Names），
  • 都是 URI 的子集。

• 属性（Properties）：属性是用来描述资源的特定特征或关系，每一个属性都有特定的意义，用来定义它的属性值（Value）和它所描述的资源形态，以及和其它属性的关系。

• 陈述（事实）（Statements）：特定的资源以一个被命名的属性与相应的属性值来描述，称为一个RDF陈述，其中资源是主语，属性是谓语，属性值则是宾语，陈述的宾语除了可能是一个字符串，也可能是其它的资料形态或是一个资源。

2.2.2. RDF 的序列化

序列化是指将数据结构保存为可读的格式，RDF 常用的序列化包括以下三种：

• Turtle 语法：对于 RDF 来说，最常用的序列化格式是 Turtle，它也是人类可读性最好的格式，推荐在开发和调试中使用：

  @prefix ex: <http://example.org/> .
  @prefix schema: <http://schema.org/> .
  
  ex:Alice a schema:Person ;
          schema:name "Alice" ;
          schema:knows ex:Bob .
  

• RDF/XML：

  <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
           xmlns:foaf="http://xmlns.com/foaf/0.1/">
    <rdf:Description rdf:about="http://example.org/person/Alice">
      <foaf:name>Alice</foaf:name>
    </rdf:Description>
  </rdf:RDF>
  

• N-Triples：这是一种非常简单的RDF语法，每行表示一个三元组，使用空格分隔主体、谓语和宾语，并且需要用尖括号 < > 括起来。即用多个三元组来表示RDF数据集。例如：

  <http://example.org/person/Alice> <http://xmlns.com/foaf/0.1/name> "Alice" .
  <http://example.org/person/JohnSmith> <http://xmlns.com/foaf/0.1/name> "John Smith" .
  

2.2.3. RDF-Schema

查看如下 RDF 资源：

# 定义一些实例（个体）
:Alice a :Person.
:Bob a :Person.
:TheGodfather a :Movie.

# 描述它们之间的关系
:Alice :likes :Bob.
:Alice :likes :TheGodfather.
:Bob :hasBirthdate "1990-01-01"^^xsd:date.

在这个层面上，我们只知道：

• 存在一个叫 Alice 的东西，它被归类为 Person。

• 存在一个叫 Bob 的东西，它也被归类为 Person。

• 存在一个叫 TheGodfather 的东西，它被归类为 Movie。

• Alice “喜欢” Bob。

• Alice “喜欢” TheGodfather。

• Bob 有一个生日是 “1990-01-01”。

但机器不知道：

• Person 和 Movie 到底是什么？它们有什么关系？

• likes 这个属性是什么意思？它可以用来连接什么类型的东西？

• hasBirthdate 这个属性的值应该是什么格式？它能被用于 Movie 吗？

也就是说 RDF 只关心陈述事实，但不关心这些事实的含义。

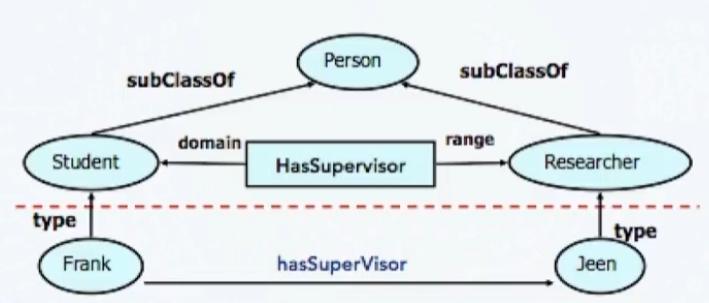
在此基础上，人们提出了 RDF-Schema（RDFS），通过引入了一组标准的词汇（本身也是一个 RDF 词汇表），用来定义我们使用的术语（类别、属性），它为数据赋予了语义。

常用的词汇表示包括：

Class, subClassOf, Property, subPropertyOf, Domain, Range, type

基于 RDFS 我们就可以进行简单的推理：

更加复杂的情况下，我们基于前面提出的 RDF 资源，使用的词汇下定义

# 首先定义一些类（Class）
:Person a rdfs:Class.
:Movie a rdfs:Class.
:CreativeWork a rdfs:Class.

# 声明类之间的层次关系（Movie 是 CreativeWork 的子类）
:Movie rdfs:subClassOf :CreativeWork.

# 定义一些属性（Property）
:likes a rdf:Property.
:hasBirthdate a rdf:Property.

# 声明属性的约束
# :likes 属性的主体（domain）可以是任何资源（范围很广）
:likes rdfs:domain :Resource.

# :likes 属性的客体（range）也可以是任何资源
:likes rdfs:range :Resource.

# :hasBirthdate 属性的主体（domain）必须是 Person
:hasBirthdate rdfs:domain :Person.

# :hasBirthdate 属性的客体（range）必须是日期值
:hasBirthdate rdfs:range xsd:date.

可以推理出：

• 从 rdfs:subClassOf 推理：

  • 已知： :Movie rdfs:subClassOf :CreativeWork. 和 :TheGodfather a :Movie.

  • 推理出： :TheGodfather a :CreativeWork. （因为电影是创意作品的子类）

• 从 rdfs:domain 推理：

  • 已知： :hasBirthdate rdfs:domain :Person. 和 :Bob :hasBirthdate "1990-01-01".

  • 推理出： :Bob a :Person. （这个推理在我们的例子中已经是显式声明的，但如果没声明，机器可以推出来）

  • 重要： 如果有人错误地写了一个三元组 :TheGodfather :hasBirthdate "1972-01-01"，推理机可以根据 rdfs:domain :Person 推断出 :TheGodfather a :Person，这显然是一个矛盾，可以帮助发现数据错误。

• 从 rdfs:range 推理：

  • 已知： :hasBirthdate rdfs:range xsd:date.

  • 当看到 :Bob :hasBirthdate "1990-01-01" 时，机器就知道 "1990-01-01" 应该被当作一个日期对象来处理，而不是一个普通的字符串。

2.2.4. OWL

OWL（Web Ontology Language）是一种用于表示和共享本体（Ontology）的标准化语言。本体是一种形式化的知识表示，用于描述领域中的概念、实体和它们之间的关系。OWL 是一种语义网络，它旨在使计算机能够更好地理解和处理信息，从而支持语义搜索、知识图谱构建、自动推理和智能应用的开发。

Ontology in Philosophy: Ontology is the philosophical study of the nature of being, becoming, existence or reality, as well as the basic categories of being and their relations.

—Merriam-Webster

Ontology in Computer Science and Artificial Intelligence: An ontology is a description (like a formal specification of a program) of the conceptsand relationships that can formally exist for an agent or a community of agents.

—Tom Gruber, Founder of Siri

Web Ontologies: Ontologies based on web standards such as RDFS/0WL. OWL is based on Description Logica very very long history of research in Artificial Intelligence.

前文介绍的 RDFS 本质上是 RDF 的一个扩展。后来人们发现 RDFS 的表达能力还是相当有限，因此提出了 OWL。我们也可以把OWL 当做是 RDFS 的一个扩展，其添加了额外的预定义词汇。

• RDF-Schema
  • Class
  • subclass
  • Property
  • subProperty
  • …
• OWL
  • Complex Class（复杂类）
    • intersection → 交（逻辑与）
    • union → 并（逻辑或）
    • complement → 补（逻辑非）
  • Property Restrictions（属性限制）
    • existential quantification → 存在量化 $\exists$
    • universal quantification → 全称量化 $\forall$
    • has Value → 值约束
  • Cardinality Restrictions（基数约束）
    • 用于定义基于属性值数量限制的类
    • maxQualifiedCardinality → 最大基数限定（至多）
    • minQualifiedCardinality → 最小基数限定（至少）
    • qualifiedCardinality → 精确基数限定
  • Property Characteristies（属性特性）
    • inverseOf → 逆属性
    • SymmetricProperty → 对称属性
    • AsymmetricProperty → 非对称属性
    • propertyDisjointWith → 属性互斥
    • ReflexiveProperty → 自反属性
    • FunctionalProperty → 函数型属性
  • Property Chains → 属性链

下面介绍几种典型的 OWL 表达构建：

• 等价性声明

  exp:运动员 owl:equivalentClass exp:体育选手
  exp:获得 owl:equivalentProperty exp:取得
  exp:李明 owl:sameIndividualAs exp:小明
  

• 声明属性的传递性

    exp:ancestor rdf:type owl:TransitiveProperty
    exp:小明 exp:ancestor exp:小林
    exp:小林 exp;ancestor exp:小志
    ==> exp:小明 exp:ancestor exp:小志.
  

• 声明两个属性互反

  exp:ancestor owl:inverseOf exp:descendant
  exp:小明 exp:ancestor exp:小林
  ==> exp:小林 exp:descendant exp:小明.
  

• 声明属性的函数型

  exp:hasMother rdf:type owl:FunctionalProperty
  

  exp:hasMother 是一个具有函数性的属性，因为每个人只有一个母亲，作为约束作用到知识库

• 声明属性的对称性

  exp:friend rdf:type owl:SymmetricProperty
  exp:小明 exp:friend exp:小林
  ==> exp:小林 exp:friend exp:小明
  

• 声明属性的局部约束：存在限定

  exp:CVPaper owl:someValuesFrom exp:CCF-A
  exp:CVWebPaper owl:onProperty exp:publishedn
  

  exp:publishedln 在主语属于 exp:SemanticWebPaper 类的时候，宾语的取值部分来自 exp:CCF-A 这个类。上面的三元组相当于「关于语义网的论文部分发表在 CCF-A 类上」

• 声明属性的局部约束：基数限定

  exp:Person owl:cardinality “1”^^xsd:integer
  exp:Person owl:onProperty exp:hasMother
  

  exp:hasMother 在主语属于 exp:Person 类的时候，宾语的取值只能有一个；“1” 的数据类型被声明为 xsd:integer。这是基数约束，本质上属于属性的局部约束。

• 声明相交的类

  exp:Mother owl:intersectionOf _tmp
  _tmp rdf:type rdfs:Collection
  _tmp rdfs:member exp:Person
  _tmp rdfs:member exp:HasChildren
  

  _tmp 是临时资源，它是 rdfs:Collection 类型,是一个容器；它的两个成员是 exp:Person、exp:HasChildren。上述三元组说明 exp:Mother 是 exp:Personexp:HasChildren 这两个类的交集。

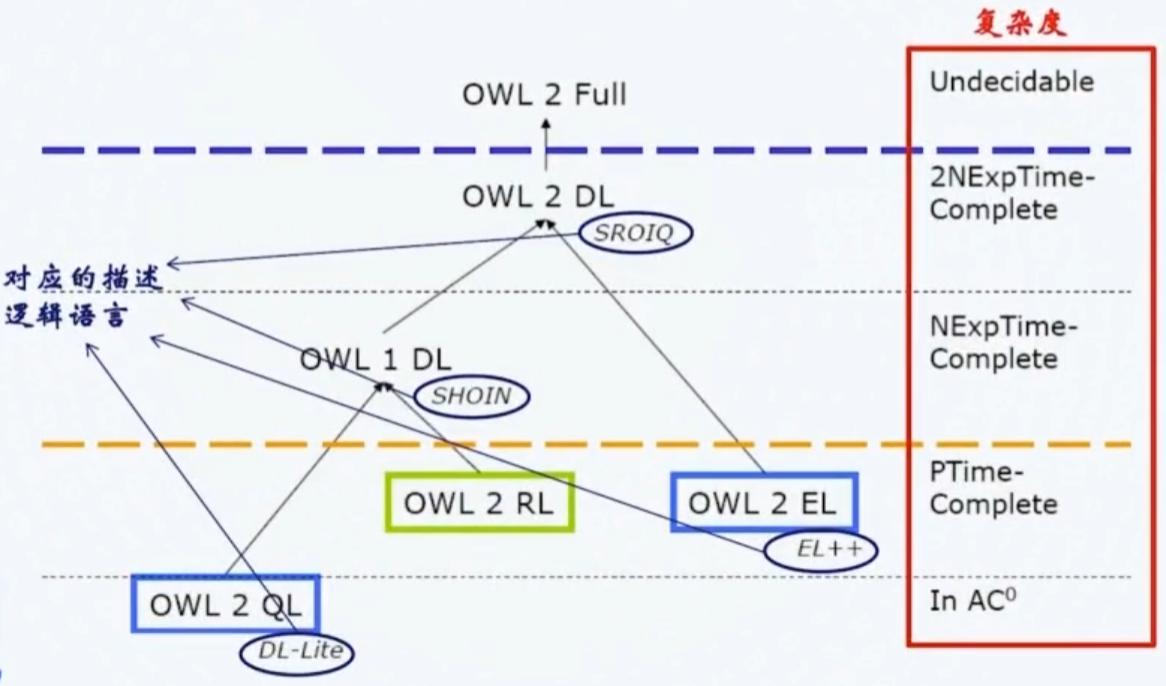
OWL 包含一系列语言家祖，每一种子语言都是前面语义表达构建的一类集合，并有相应的复杂度分析。

如图，

• OWL 2 QL 是 OWL 语言的子集，它只包含基本的语义表达，如类、属性、数据类型等，专为大规模查询（Query）设计
• OWL 2 RL 是 OWL 语言的子集，在扩展 RDFS 表达的同时，保持了较低的复杂度，常被用于规则的推理（Reasoning）设计
• OWL 2 EL 专为概念术语（EL++）推理而设计，常用于生物医疗领域

2.2.5. 总结

最后，整理 RDF 相关概念之间的关系如下图所示：

flowchart LR
    A[RDF] --规则<br>（Class，Property, ...）--> B["RDF-Schema (RDFS)"]

    B -- 更复杂规则+关系<br>(Complex Class, ...) --> C[OWL]

2.3. 基于嵌入的表示

3. 知识推理

4. 知识图谱

5. 参考文献

[1] bilibili 知识图谱