图像分类是计算机视觉领域的基础任务,旨在通过算法自动识别图像中包含的目标类别。卷积神经网络(CNN)凭借其强大的特征提取能力,已成为图像分类的主流方法。本文将详细介绍CNN用于图像分类的原理、典型网络架构及实践要点。
1. 图像分类基础
1.1. 任务定义
图像分类是指给定一张输入图像,通过算法判断该图像属于预定义类别集合中的哪一类。从数学角度看,图像分类可视为一个映射函数:
\[f: I \rightarrow C\]其中,$I$ 表示输入图像(通常表示为像素值矩阵),$C$ 表示类别集合(如 {猫, 狗, 汽车, …})。
根据类别数量可分为:
- 二分类:仅有两个类别(如猫/狗分类)
- 多分类:三个及以上类别(如ImageNet的1000类分类)
- 多标签分类:图像可同时属于多个类别(如一张图片中同时包含猫和狗)
实际上,网络(模型)对输入图像进行预测时,会返回一个概率向量,该向量中包含所有类别的概率。我们必须要指定一个阈值,将概率向量中的概率映射为二分类结果。这个阈值被称为「置信度阈值」(Threhold)。置信度阈值决定了如何将概率转化为类别标签。
一般而言,概率大于阈值的样本为正例,小于阈值的样本为负例。
1.2. 性能指标
评估图像分类模型性能的核心指标包括:
1.2.1. 准确率
准确率(Accuracy) 是最朴素的性能指标,计算公式为:
\[\text{Accuracy} = \frac{\text{正确分类的样本数}}{\text{总样本数}}\]1.2.2. 混淆矩阵
以二分类为例,样本的真实标签包括两个类别:「正」和「负」,同样网络预测的类别也有两个类别:「正」和「负」。按照这两个维度可以形成四种情况,列表如下:
| 真实值 | 真实值 | ||
|---|---|---|---|
| 正 | 负 | ||
| 预测值 | 正/P | (真正例)TP | (假正例)FP |
| 预测值 | 负/N | (假负例)FN | (真负例)TN |
上面的表格就是 混淆矩阵(Confusion Matrix),其展示各类别间的分类错误分布。
一个小技巧:所有的第二个大写英文字母(Positive 或者 Negative)都是预测的结果,再根据预测是否正确确定第一个英文字幕是 True 还是 False。
思考:混淆矩阵可以有多少个?
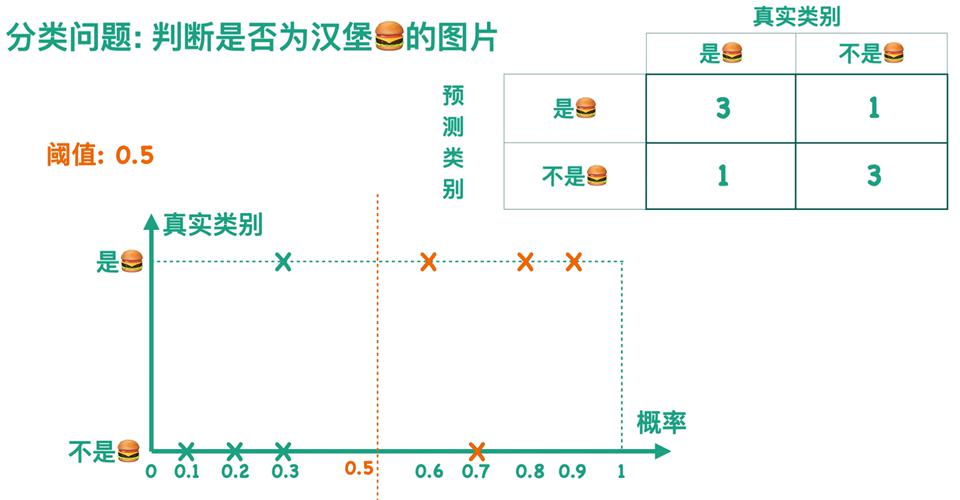
假设阈值为 $0.5$,即预测概率大于 $0.5$ 的样本被判定为「正」,否则为「负」,此时可以得到一个混淆矩阵。如下图所示,对于一批 $8$ 张图片,判断其是否为汉堡,结果如下可以得到图中的混淆矩阵。
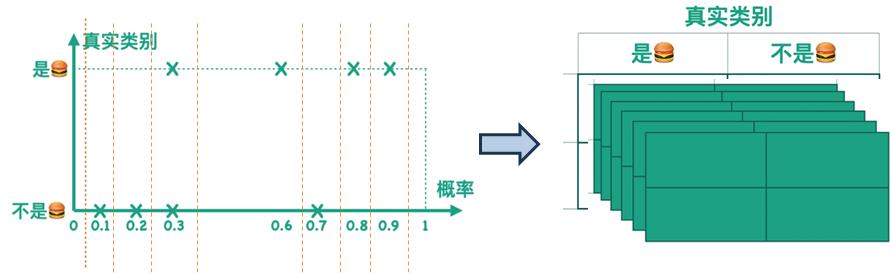
类似地,完全可以设置阈值为更加严格的 $0.75$,此时可以得到另一个混淆矩阵。以此类推,连续地将阈值从比如 $0.01$ 一直递增,直到 $0.99$,可以得到许许多多个混淆矩阵。
这导致直接使用混淆矩阵来评估模型性能比较麻烦。因此引入第二个问题:能否把所有混淆矩阵表示在同一个二维空间呢? 这需要借助后面介绍的两个特殊性能指标:精确率(Precision)与召回率(Recall)。
思考:按照混淆矩阵如何重新定义准确率?
\[\text{Accuracy} = \frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}\]1.2.3. 精确率与召回率
在混淆矩阵的基础上,我们分别讨论两种特殊的性能指标,即精确率和召回率。
-
精确率 / 查准率(Precision):
当我们关心,所有「预测为正」的样本中,有多少比例的样本是「真实的正」样本时,可定义精确率指标如下:
\[\text{Precision} = \frac{\text{真正例(TP)}}{\text{真正例(TP)+ 假正例(FP)}}\]对应混淆矩阵中:
真实值 真实值 正 负 预测值 正/P (真正例)TP (假正例)FP 预测值 负/N (假负例)FN (真负例)TN 精确率越高,意味着预测值中正样本预测的越准。
-
召回率 / 查全率(Recall):
类似地,如果我们反向思考,关心所有「真实的正」样本中,有多少样本被模型「预测为正」,此时得到召回率指标如下:
\[\text{Recall} = \frac{\text{真正例(TP)}}{\text{真正例(TP)+ 假负例(FN)}}\]对应混淆矩阵中:
真实值 真实值 正 负 预测值 正/P (真正例)TP (假正例)FP 预测值 负/N (假负例)FN (真负例)TN 召回率越高,意味着所有「真实的正」的样本中,有越多的样本被网络(模型)给正确预测出来。
下面讨论置信度阈值与上述两个指标的关系。
提高置信度阈值(Threshold),模型变得更“保守”,只有非常确定的样本才被预测为正例。这会导致:
- 精确率上升(因为FP减少)
- 召回率下降(因为一些正例因为不够确定而被漏掉,FN增加)
降低置信度阈值,模型变得更“激进”,更多样本被预测为正例。这会导致:
- 召回率上升(因为FN减少)
- 精确率下降(因为FP增加)
所以置信度阈值是权衡精确率和召回率的关键因素。下一节我们专门讨论置信度阈值的影响和一个新的性能指标:PR 曲线。
1.2.4. PR 曲线
PR 曲线(Precision-Recall Curve)是不同阈值下 Precision 与 Recall 的关系曲线:
- 横轴:Recall(召回率)
- 纵轴:Precision(精确率)
- 绘制方法:遍历所有可能的阈值,计算对应 Precision 和 Recall,连接成曲线。通常可以对所有样本进行排序,再逐个样本的选择阈值,在该样本之前的都属于正例,该样本之后的都属于负例。
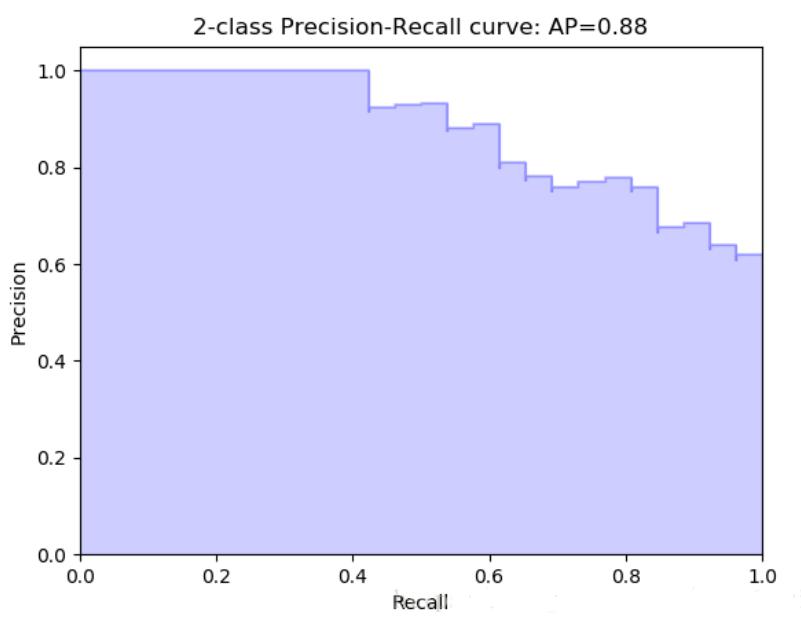
下面给出了一个 PR 曲线的实例:
下面分析 PR 曲线的一些特点:
-
当阈值为 $0$ 时,模型将所有样本都预测为正例,此时召回率为 $100\%$,精确率与样本集中正负样本的比例有关,等于正样本所占的比例,PR 曲线会从右侧某个点开始。一般 PR 曲线不会经过 $(1,0)$ 点,除非正样本占比十分少。
- 当阈值为 $1$ 时,
-
首先考虑理想情况,即对所有「真实为正」的样本的预测概率(网络输出)都为 $100\%$,此时精确率和召回率均为 $1$,PR 曲线会经过(右上角) $(1,1)$ 点。
-
其次考虑实际情况,即对所有「真实为正」的样本的预测概率(网络输出)肯定到不了 $100\%$,此时精确率为 $0$,召回率自然也为 $0$(没有一个真正的真样本被预测对),曲线抵达(左下角) $(0,0)$ 点的下方。
-
随着阈值从 $1$ 逐渐开始降低,总会有个一个预测概率最高的样本(一般而言也是预测正确的)高于了设定的阈值,此时精确率为 $1$;召回率很小,因为绝大部分正样本都被很高的阈值给挡住,错判成了负样本了。所以曲线会从(左下角) $(0,0)$ 点瞬间跳变到接近(左上角)$(0,1)$ 点。
-
- 随着阈值继续降低,
- 召回率非递减(递增或不变),因为随着阈值的降低,正例的判定更宽松,更多的真正的正例被正确识别(FN 变少);
- 精确率的整体趋势是降低的,但不是严格非递增,而是会存在震荡,因为虽然正例被判为正例的变多,但负例被判为正例的也变多了。
- 一个特殊情况:如果样本数据很简单、网络(模型)训练的很好,导致存在一个阈值可以完全区分正例和负例,此时 PR 曲线覆盖的面积就是整个矩形空间。
总结:P-R曲线应该是从 $(0,0)$ 开始画的一条曲线,切割 $1\times 1$ 的正方形,得到一块区域。
如何通过 PR 曲线比较两个不同的模型性能呢?曲线越靠近右上角(即曲线下方的面积越大),模型的性能就越好。
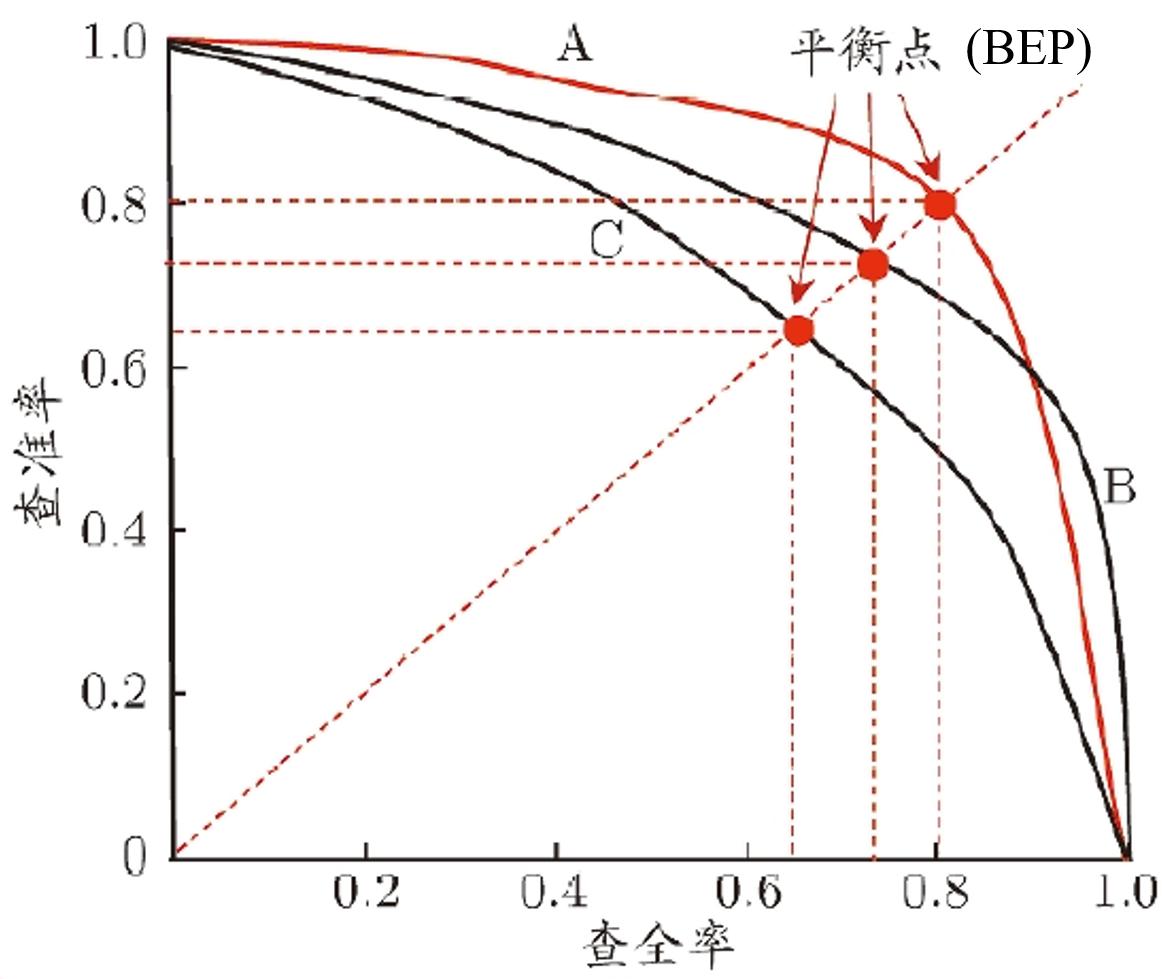
观察下图,有两种判别方式:
- 基于包裹的判别方式:如果一条 PR 曲线完全包裹另外一条 PR 曲线,则该 PR 曲线对应的网络(模型)性能更好;
- A 完全包裹 C,则 A 模型性能更好
- B 完全包裹 C,则 B 模型性能更好
- A 和 B 之间相互有重叠,无法判断哪个模型性能更好
- 基于平衡点(Break-Even Point, BEP)的判别方式:连接左下角和右上角两个顶点,与 PR 曲线的交点称为平衡点。平衡点是 Precision(查准率)和 Recall(查全率)相等时的点。这个点提供了一个综合考量查准率和查全率的性能度量,因为在平衡点上,两个指标达到相同的数值,从而为分类器性能评估提供了一个直观的参考点。平衡点的值越大,则模型性能更好;
- A 模型性能更好
- B 模型性能居中
- C 模型性能最差
1.2.5. F1 分数
注意到,Precision 和 Recall 是相互制约的两个指标,且需要对阈值进行遍历才能完成绘制。有时候我们不想绘制繁琐的 PR 曲线,而是希望直接比较给定阈值下的模型性能,此时可以采取一个新的指标:F1 分数(F1 score)。
$F1$分数 是对精确率和召回率的调和平均,其计算公式如下:
\[F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]如果对查准率和查全率有不同的偏好,可以使用改进的 $F_\beta$ 分数:
\[F_\beta = \frac{(1 + \beta^2) \times \text{Precision} \times \text{Recall}}{\beta^2 \times \text{Precision} + \text{Recall}}\]当 $\beta>1$ 时,对召回率(查全率)偏好较大,反之对精确率(查准率)更偏好。
1.2.6. FPR 和 TPR
和 Precision / Recall 类似,我们还可以定义另外一组性能指标:
-
FPR(False Positive Rate,假阳率):在所有实际为负例的样本中,被网络(模型)错误预测为正例的概率:
\[FPR = \frac{FP}{FP + TN}\]对应混淆矩阵中:
真实值 真实值 正 负 预测值 正/P (真正例)TP (假正例)FP 预测值 负/N (假负例)FN (真负例)TN -
TPR(True Positive Rate,真阳率 = 查全率 / 召回率):在所有实际为正例的样本中,被网络(模型)正确预测为正例的概率。
类似于 PR 曲线,采用 FPR 和 TPR 也可以定义一个新的曲线:ROC(Receiver Operating Characteristic)曲线。
1.2.7. ROC 曲线
以 FPR 为横轴,TPR 为纵轴,可以定义新的曲线 「ROC(Receiver Operating Characteristic)曲线」。
一般情况下,这个曲线都应该处于 $(0, 0)$ 和 $(1, 1)$ 连线的上方。ROC曲线越接近左上角,模型效果越好。
$(0, 0)$ 和 $(1, 1)$ 连线形成的 ROC 曲线实际上代表的是一个随机分类器。如果ROC曲线位于对角线下方,表明模型结果劣于随机分类。在这种情况下,可以考虑将二分类结果进行互换以改善模型性能。
通过分析ROC曲线下的面积(AUC, Area Under the Curve),可以直接比较不同模型的优劣。AUC越大,模型的分类性能越优越。
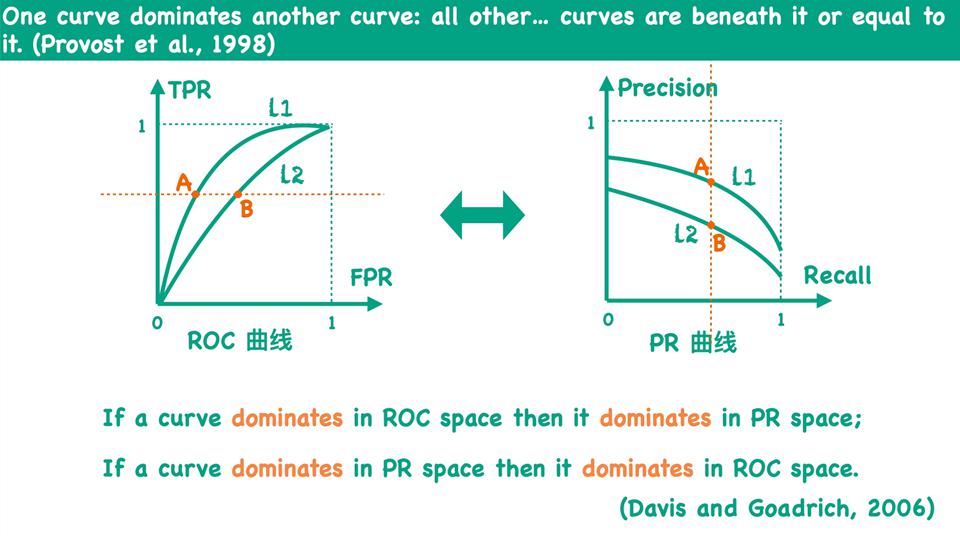
与 PR 曲线相比,ROC 曲线也可以用来比较网络(模型)的性能,且有如下结论:如果一个网络(模型)的曲线在 PR 域下更优,那么其在 ROC 域下也更优,反之亦然:
既然如此,为何又要重复定义一个 ROC 曲线呢?因为 ROC 曲线和 PR 曲线在某些场景下的性能评判效果不一样。具体地,在正负样本的分布极为不均的情况下,与 ROC 曲线相比,PR 曲线能更有效地反映模型的整体分类效果。
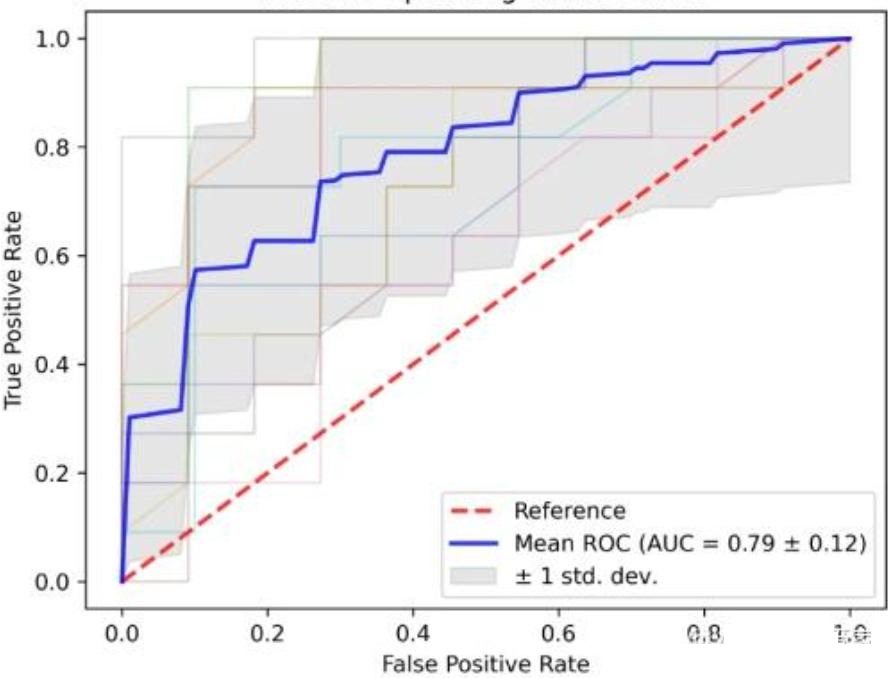
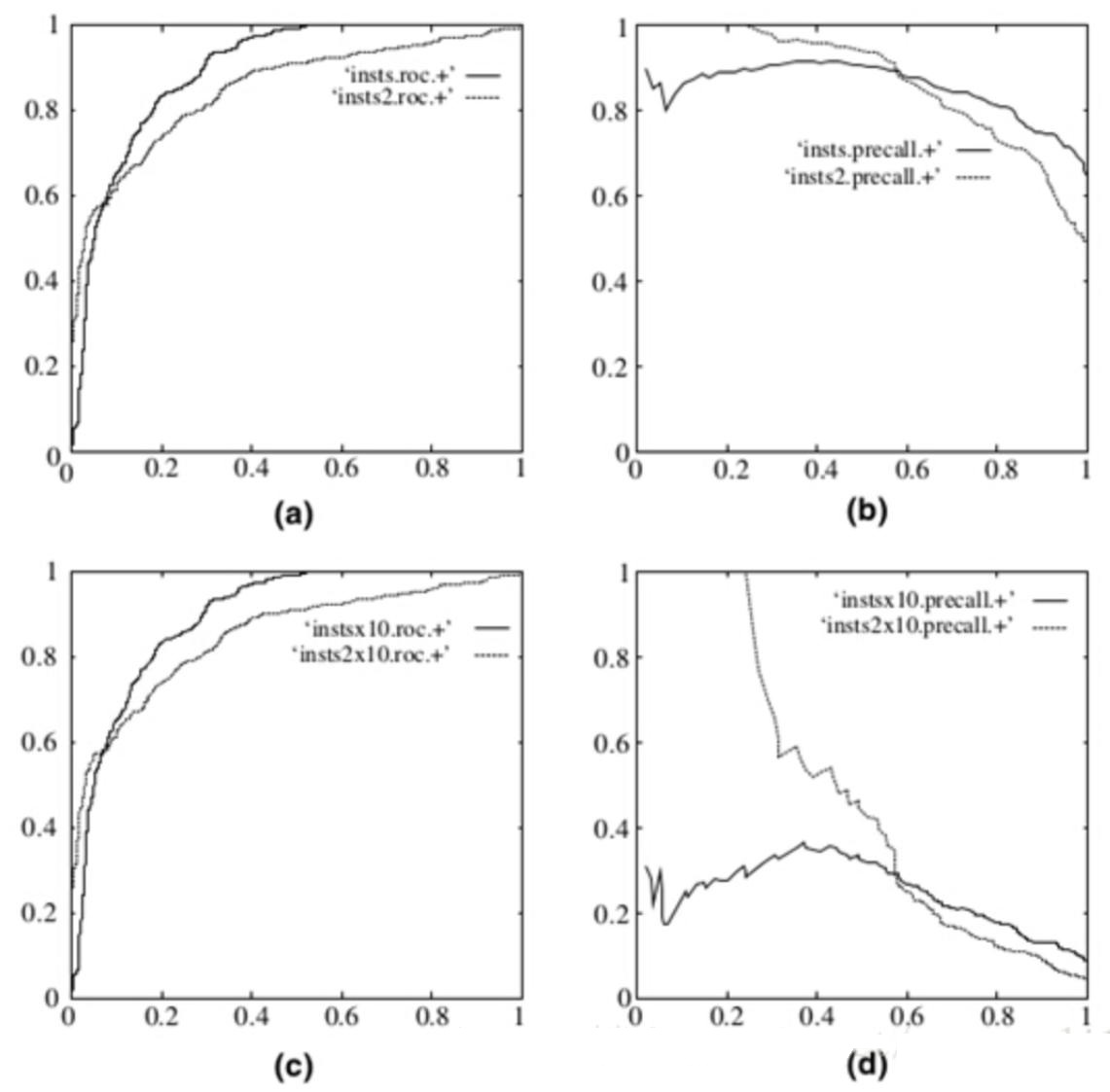
在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是 ROC 曲线和 PR 曲线的对比:
其中第一行(a)(b)均为原数据的图,左边为 ROC 曲线,右边为 PR 曲线。第二行(c)(d)为负样本增大 $10$ 倍后俩个曲线的图。可以看出,ROC 曲线基本没有变化,但 PR 曲线确剧烈震荡。因此,在面对正负样本数量不均衡的场景下,ROC 曲线(AUC 的值)会更加稳定。
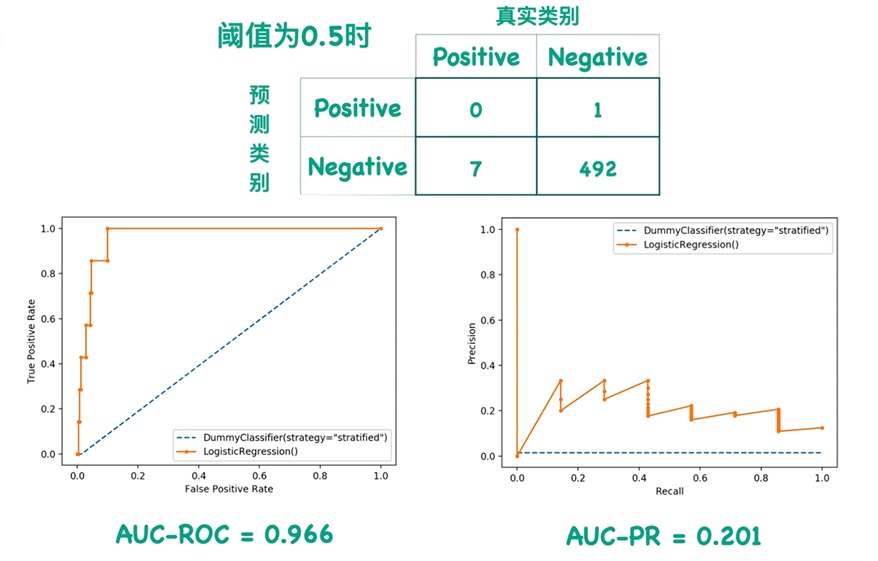
下面给一个具体的示例,在阈值 $0.5$ 时,几乎所有($500$ 中的 $493$ 个)样本为负例,网络(模型)对仅有的 $7$ 个正例都预测错误。此时绘制 ROC 曲线和 PR 曲线如下:
可以看出,虽然正例一个都没预测对,但ROC曲线看着依然很好,反观 PR 曲线会很差。因此,如果:
- 不关心负样本占比 / 性能(或数据均衡),优先选 ROC 曲线(AUC);
- 若关心负样本相关性能(如数据极度不平衡、重视正样本的精确性),优先选 PR 曲线(AUPR)。
1.3. 多分类问题
当我们的任务有 $K$ 个类别时,评估变得复杂。我们有两种主要的平均策略:宏平均 和 微平均。
首先,对于每个类别 $i$,我们都可以将其视为一个「二分类」问题(One-vs-Rest,OvR,类别 $i$ 为正类,其他所有类别为负类),计算出该类别下的 $TP_i$、$FP_i$、$FN_i$、$TN_i$。$K$ 个类别可以得到 $K$ 组二分类器的性能指标 $(TP_i$、$FP_i$、$FN_i$、$TN_i)$ 元组。
- 类别视角:为每个类别分别都构建一个二分类器。也即对于每一组二分类其的性能指标,可以计算查准率、查全率和 $F1$ 分数,然后求平均值,记为宏观指标:
- 样本视角:将每个样本在所有二分类任务中得到的性能指标元组分别相加,视为一个全局的二分类问题。然后计算一个统一的指标,记为微观指标:
最后通过表格来比较:
| 特性 | 宏观平均 | 微观平均 |
|---|---|---|
| 样本量影响 | 平等看待每个类。小类别的性能对最终指标有同等影响力。 | 受大类主导。大类别(样本多)的性能对指标影响大。 |
| 实质 | 衡量的是每个类别的平均性能。 | 衡量的是每个样本的分类是否正确。 |
| 在类别不平衡时的倾向 | 能更好反映小类别的性能。即使大类别全对,一个小类别全错也会拉低宏平均指标。 | 更接近大类别的性能。如果大类别分类得好,微观指标就高。 |
| 使用场景 | 1. 平等重视每一个类别 2. 存在严重类别不平衡且关心小类别 3. 想知道模型在所有类别上的平均表现 |
1. 关心整体模型性能,每个样本权重相同 2. 类别不平衡但小类别不重要 3. 只需要简单“准确率”概念 |
在通过表格来给出不同问题中的选择建议:
| 场景 | 推荐指标 | 理由 |
|---|---|---|
| 医疗诊断(罕见病检测) | 宏观平均 | 罕见病(小类别)的检测至关重要,需要平等关注每个疾病类别 |
| 新闻主题分类(政治类占80%) | 宏观平均 | 需要评估模型对小类别(如科技、体育)的分类能力,避免被政治类主导 |
| 客户流失预测(流失率5%) | 两者结合 | 宏观F1看对小类(流失客户)的识别能力,微观F1看整体准确率 |
| 垃圾邮件过滤(垃圾邮件占10%) | 微观平均 | 更关心整体过滤效果,每个邮件的处理都同等重要 |
| 图像分类(ImageNet) | 宏观平均 | 需要平等评估模型对1000个类别的识别能力,避免被大类主导 |
| 推荐系统CTR预测 | 微观平均 | 每个用户请求同等重要,关心整体预测准确性 |
1.4. 优势与挑战
与传统图像分类方法(手动设计特征+分类器)相比,CNN的端到端学习具有显著优势:
- 无需人工设计特征提取器,特征和分类器联合优化
- 能够自动学习任务相关的判别性特征
- 随着网络加深,可捕捉从低级到高级的多层次特征
- 对数据分布变化具有更好的适应性
图像分类面临的主要挑战包括:
- 类内差异:同一类别的图像在姿态、光照、尺度等方面存在差异
- 类间相似:不同类别的图像可能具有相似的视觉特征
- 背景干扰:复杂背景可能掩盖目标特征
- 样本不平衡:部分类别的样本数量远少于其他类别
- 遮挡(occlusion):目标被部分遮挡导致特征不完整
- 视角变化:同一目标从不同视角拍摄呈现不同外观
2. 典型CNN图像分类网络
2.1. LeNet-5
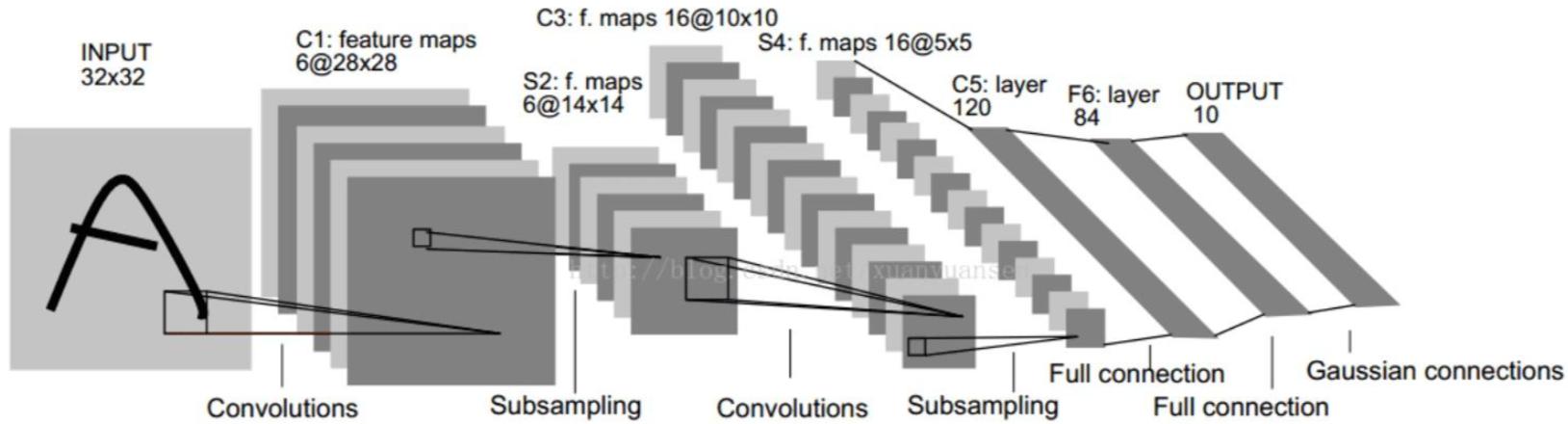
LeNet-5 是 Yann LeCun 于 1998 年提出的首个卷积神经网络,主要用于手写数字识别(MNIST 数据集)。
网络结构:
- 输入层:$32 \times 32 \times 1$(灰度图像,归一化)
- C1层:6个 $5 \times 5$ 卷积核,步长1,输出 $28 \times 28 \times 6$
- S2层:$2 \times 2$ 平均池化,步长2,输出 $14 \times 14 \times 6$
- C3层:16个 $5 \times 5$ 卷积核,步长1,输出 $10 \times 10 \times 16$
- S4层:$2 \times 2$ 平均池化,步长2,输出 $5 \times 5 \times 16$
- C5层:120个 $5 \times 5$ 卷积核,输出 $1 \times 1 \times 120$(等效全连接)
- F6层:84个神经元的全连接层
- 输出层:10个神经元(对应10个数字),使用softmax激活
特征图的大小与输入图像尺寸、卷积核尺寸、卷积核个数、移动步长均有关。假设输入图像尺寸为 $N\times N$,卷积核大小为 $F\times F$,卷积核个数为 $M$,移动步长(stride)为 $S$,则经过卷积操作后的特征图大小为
\[\lfloor\frac{N-F}{S}+1 \rfloor \times \lfloor\frac{N-F}{S}+1 \rfloor\times M\]其中 $\lfloor \cdot \rfloor$ 表示向下取整操作。
特点:
- 首次将卷积、池化、全连接结合形成完整网络
- 采用权值共享减少参数量
- 奠定了现代CNN的基本框架
2.2. AlexNet
AlexNet 由 Alex Krizhevsky 等人于 2012 年提出,在 ImageNet 竞赛中大幅超越传统方法,开创了深度学习在计算机视觉的新时代。
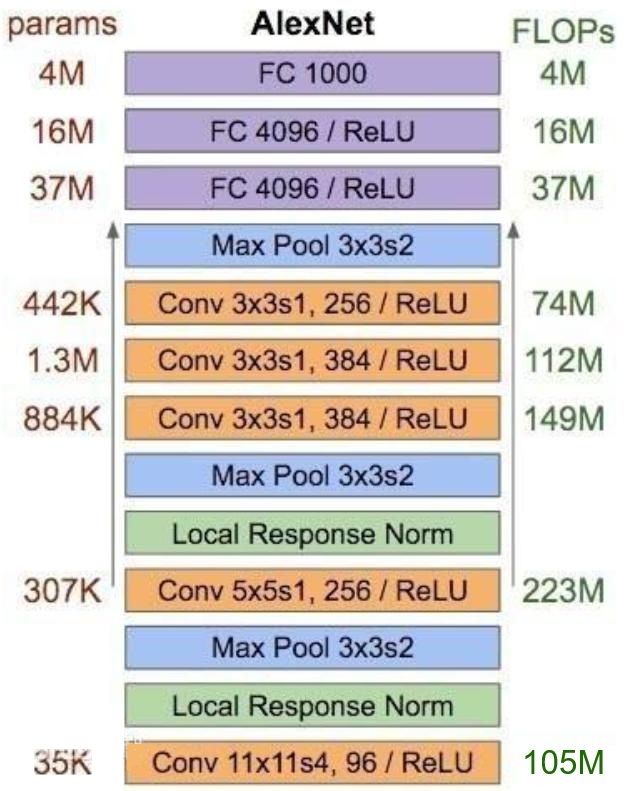
网络结构:
- 输入层:$227 \times 227 \times 3$(填充后的 RGB 图像)
- 5个卷积层 + 3个全连接层
- 关键配置:
- 第1层:96个 $11 \times 11$ 卷积核,步长4(卷积后特征图尺寸为 $55\times 55\times 96$,因为 $(227-11)/4+1=55$)
- 第2层:256个 $5 \times 5$ 卷积核,带填充
- 第3-5层:384、384、256个 $3 \times 3$ 卷积核
- 全连接层:4096 → 4096 → 1000(类别数)
考虑偏置加法运算的卷积计算量(FLOPs)如下:
\[FLOPs = H_{out}\times W_{out}\times C_{out}\times 2\times K^2\times C_{in}\]易知,标准卷积的参数量(param)为
\[C_{in}\times K^2\times C_{out}\]
验证计算,第一层参数量和计算量与图中是否一致:
- 参数量:$3\times 11^2\times 96 = 34848\approx 35 K$
- 计算量:$55\times 55\times 96\times 2\times 11^2\times 3 = 210830400\approx 210 M$
验证计算的结果正好是图中结果的两倍。因此,图中虽然标注是 FLOPs,但实际计算量采用的是 MACs(乘加)。
创新点:
- 采用 ReLU 激活函数,解决 sigmoid 的梯度消失问题
- 引入 Dropout(概率0.5)防止过拟合
- 使用重叠池化(步长 < 池化窗口)提升特征提取能力
- 采用数据增强(平移、翻转、裁剪)扩充训练集
- 首次使用 GPU 加速训练
2.3. VGGNet
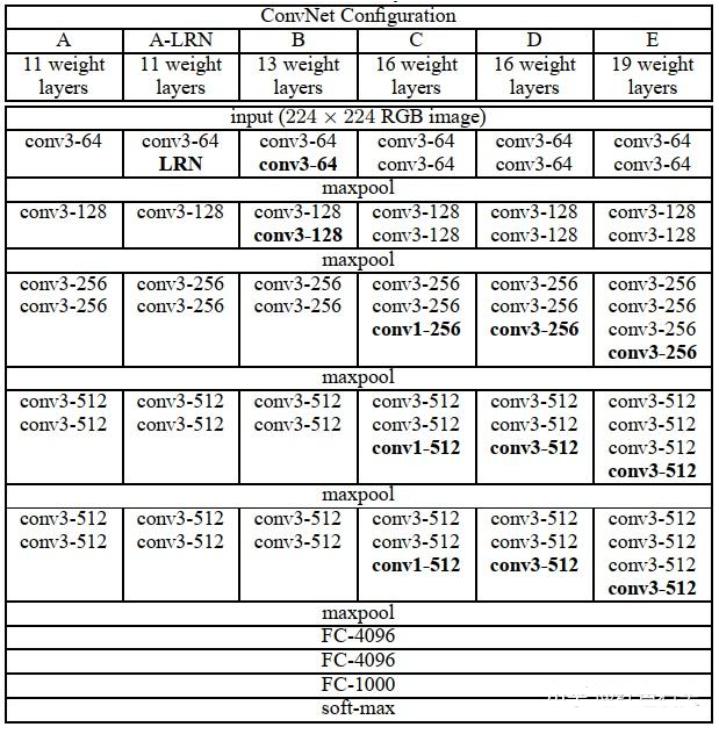
VGGNet 由牛津大学 VGG 团队于 2014 年提出,以其简洁统一的结构设计闻名。
网络特点:
- 仅使用 $3 \times 3$ 卷积核和 $2 \times 2$ 池化
- 通过增加卷积层数量加深网络(11、13、16、19层)
- 所有卷积层采用 same padding(填充 1),保持特征图尺寸
- 池化层采用 $2 \times 2$ 窗口,步长2,使特征图尺寸减半
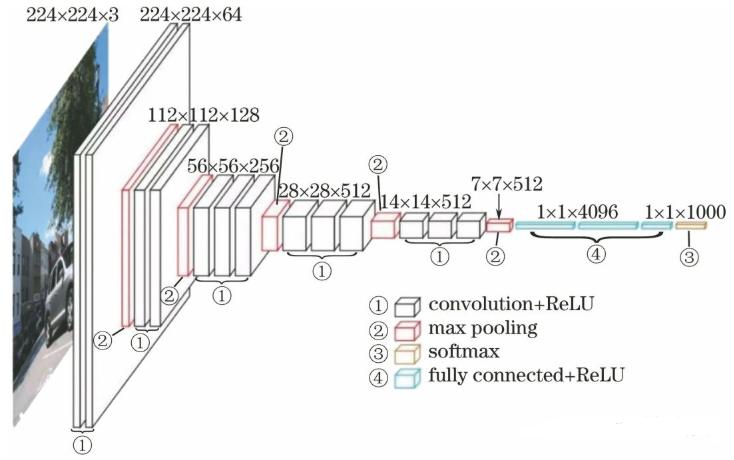
VGG-16(D系列)结构:
- 输入:$224 \times 224 \times 3$
思考:最后一层池化层后,到第一个全连接层,是如何连接的?
| 层(Layer) | 类型与参数 | 输出尺寸 (H×W×C) | 参数量(约) | MACs(约,单位 M) |
|---|---|---|---|---|
| Block 1 | Conv 3×3, 64 / ReLU | 224×224×64 | 1,792 | ~173 M |
| Conv 3×3, 64 / ReLU | 224×224×64 | 36,928 | ~173 M | |
| MaxPool 2×2 s2 | 112×112×64 | 0 | - | |
| Block 2 | Conv 3×3, 128 / ReLU | 112×112×128 | 73,856 | ~173 M |
| Conv 3×3, 128 / ReLU | 112×112×128 | 147,584 | ~173 M | |
| MaxPool 2×2 s2 | 56×56×128 | 0 | - | |
| Block 3 | Conv 3×3, 256 / ReLU | 56×56×256 | 295,168 | ~173 M |
| Conv 3×3, 256 / ReLU | 56×56×256 | 590,080 | ~173 M | |
| Conv 3×3, 256 / ReLU | 56×56×256 | 590,080 | ~173 M | |
| MaxPool 2×2 s2 | 28×28×256 | 0 | - | |
| Block 4 | Conv 3×3, 512 / ReLU | 28×28×512 | 1,180,160 | ~173 M |
| Conv 3×3, 512 / ReLU | 28×28×512 | 2,359,808 | ~173 M | |
| Conv 3×3, 512 / ReLU | 28×28×512 | 2,359,808 | ~173 M | |
| MaxPool 2×2 s2 | 14×14×512 | 0 | - | |
| Block 5 | Conv 3×3, 512 / ReLU | 14×14×512 | 2,359,808 | ~86 M |
| Conv 3×3, 512 / ReLU | 14×14×512 | 2,359,808 | ~86 M | |
| Conv 3×3, 512 / ReLU | 14×14×512 | 2,359,808 | ~86 M | |
| MaxPool 2×2 s2 | 7×7×512 | 0 | - | |
| FC 层 | Flatten | 25088 | 0 | - |
| FC 4096 / ReLU | 4096 | 102,764,544 | ~103 M | |
| FC 4096 / ReLU | 4096 | 16,781,312 | ~17 M | |
| FC 1000 (softmax) | 1000 | 4,097,000 | ~4 M | |
| 总计 | 13 Conv + 3 FC + 5 Pool | - | ~138M | ~15.5 G |
优势:
- 结构统一,易于理解和实现
- 小卷积核多次堆叠等效于大卷积核,但参数量更少。小卷积核是 VGG 的一个重要特点,VGG没有采用 AlexNet 中比较大的卷积核尺寸(如 $7\times 7$),而是通过降低卷积核的大小($3\times 3$),增加卷积子层数来达到同样的性能(VGG:从 1 到 4 卷积子层,AlexNet:1 子层)。
- 特征提取能力强,特征图保留更多细节信息
2.4. GoogLeNet
GoogLeNet 由 Google 团队于 2014 年提出。它在 ILSVRC 2014(ImageNet 大规模视觉识别挑战赛)中取得了第一名,表现优于当时的 AlexNet 和 VGGNet。GoogLeNet 的核心创新在于 Inception 结构,GoogLeNet 通过 Inception 结构 提高特征提取能力,采用更深但高效的网络,使用全局平均池化减少参数,引入辅助分类器促进训练,并以更少的计算量实现优越性能。
2.4.1. Inception 模块
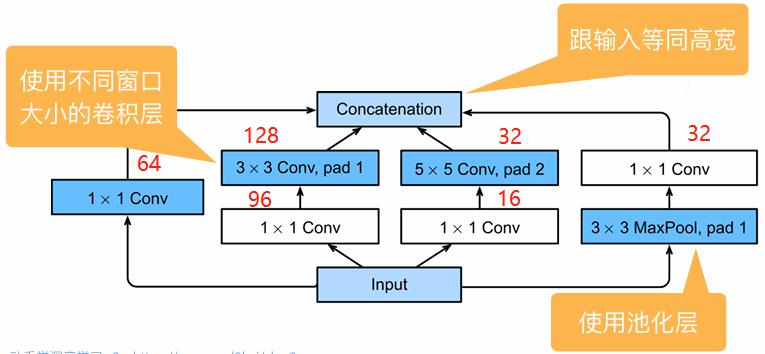
传统的卷积神经网络通常堆叠连续的卷积层。随着网络加深,参数量和计算量急剧增加,且难以确定最优的卷积核尺寸(应该用 $3\times 3$、$5\times 5$ 还是 $7\times 7$?)为此,谷歌提出:”为什么不让网络自己选择?” 至此设计了 Inception 模块,并行使用多种尺寸的卷积核,让网络自适应地学习最佳特征组合。
图中左侧(a)是初始的版本,并行使用不同尺寸的卷积核($1\times 1$、$3\times 3$、$5\times 5$)和池化操作,最后在通道维度进行拼接得到最终输出。
但是,上述改进依然存在问题,
- $5\times 5$ 卷积在深层特征图上计算量巨大
- 池化层输出通道数与输入相同,拼接后通道数爆炸性增长
- 总计算量仍然很高
针对上述问题,Google 设计了改进版本,引入 $1\times 1$ 卷积进行降维。如上图(b)所示。引入 $1\times 1$ 卷积的好处在于:
- 降维(Dimensionality Reduction):减少输入通道数,降低后续卷积的计算量
- 非线性增强:$1\times 1$ 卷积后接 ReLU 激活函数,增加了网络的非线性表达能力
- 跨通道信息整合:融合不同通道的特征信息
假设输入为 $28\times 28\times 256$,输出通道为 $64$,进行计算量对比
\[28\times 28\times 256 \times 5\times 5\times 64 \approx 321 M (MACs)\]
- 原始版本($5\times 5$ 卷积直接计算)
\[\begin{aligned} 1\times 1 \text{conv}:& 28\times 28\times 16 \times 1 \times 1 \times 256 \approx 3.2 M (MACs) \\ 5\times 5 \text{conv}:& 28\times 28\times 64 \times 5 \times 5 \times 16 \approx 20.0 M (MACs) \\ \end{aligned}\]
- 改进版本(16 通道 $1\times 1$ 卷积 + 64通道 $5\times 5$ 卷积)
总计算量降低约 $13.8$ 倍!
GoogLeNet 使用了 9 个 Inception 模块,是第一个达到上百层的网络,后续还有一系列改进。
2.4.2. 全局平均池化(GAP)
对于最后一个卷积层输出 $X \in \mathbb{R}^{H\times W\times C}$:
\[GAP(X)_C = \frac{1}{H\times W}\sum_{i=1}^{H}\sum_{j=1}^{W}X_{i,j,C}\]也即每个通道的所有空间位置取平均,直接得到 $C$ 维向量。
| 作用 | 说明 | 优势 |
|---|---|---|
| 1. 大幅减少参数量 | 消除全连接层 | AlexNet FC 层有 5800 万参数,GoogLeNet 仅用 GAP+FC(1000) ≈ 100 万参数 |
| 2. 降低过拟合风险 | 减少参数约 95% | 模型更小,泛化能力更强 |
| 3. 空间位置鲁棒性 | 对所有空间位置等权重平均 | 对输入物体的平移、小尺度变化更鲁棒 |
| 4. 强制特征映射与类别关联 | 每个通道对应一个类别特征 | 增加特征可解释性(类似 Class Activation Mapping) |
| 5. 输入尺寸灵活性 | 不依赖固定输入尺寸 | 可以处理不同分辨率的输入(自适应池化到1×1) |
2.4.3. 总结
总结 GoogleNet 的优势如下:
- 多尺度特征融合:不同尺寸卷积核捕捉不同尺度特征
- $1\times 1$ 卷积降维:减少参数量和计算量
- 增加网络宽度而非仅增加深度,提升特征多样性
2.5. ResNet
ResNet 由微软团队于 2015 年提出,通过残差连接(Residual Connection)解决了深层网络训练难题,可训练超过 $1000$ 层的网络。
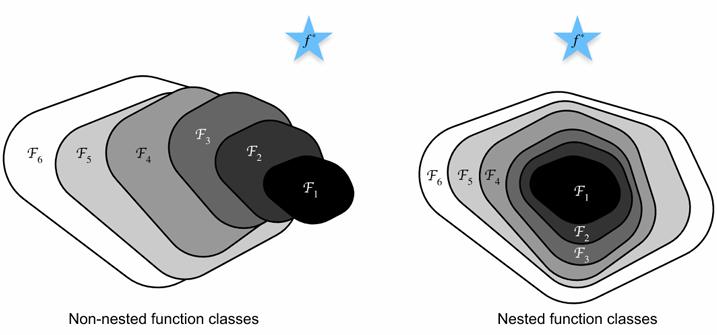
人们关于 CNN 网络有一个共同的问题:加更多的层数总是能改进精度么?观察如下图,在统计机器学习中,出现 “退化问题”(Degradation Problem)。即随着模型复杂度的增加,训练误差在更深网络上反而变高。反之,如果每次增加模型复杂度,都能完全包裹住原先简单的模型,那么至少能保证模型性能不会变差。
2.5.1. 残差块
核心创新:残差块(Residual Block)
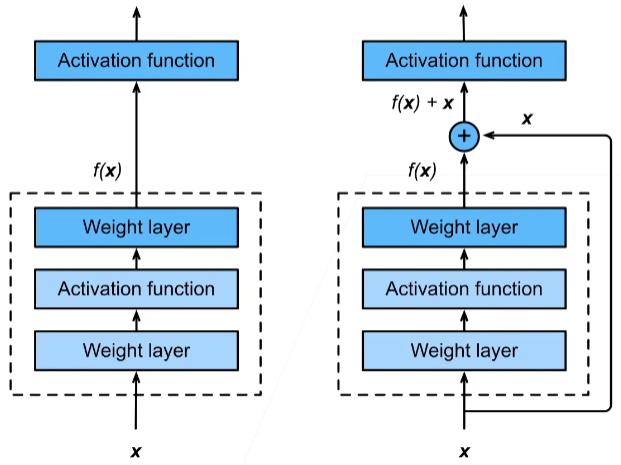
残差块通过跳跃连接(Skip Connection)使网络学习残差映射:
\[y = f(x, \{W_i\}) + x\]其中 $f(x)$ 是残差函数,$x$ 是输入,$y$ 是输出。当输入输出维度不同时,通过1×1卷积调整维度:
\[y = f(x, \{W_i\}) + W_s x\]通过残差块,即使网络结构中的 $f(x)$ 没有学到任何有用的东西,原始信息 $x$ 也可以通过残差链接得到保留,模型至少不会因为丢失信息变得更差。
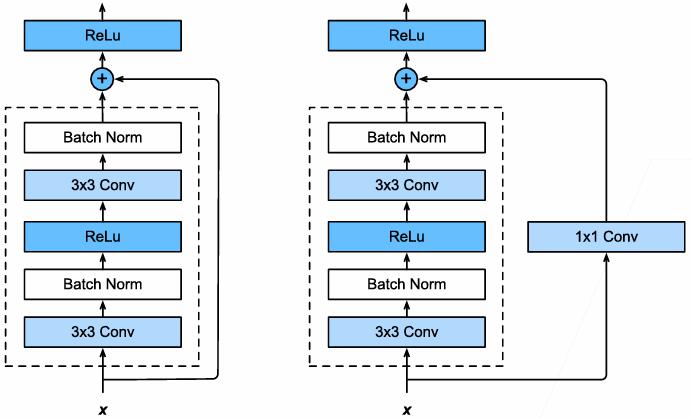
残差块中还存在一种变体,如果原本 $f(x)$ 中的卷积改变了输入的维度(如高度、宽度、通道数),那么可以在残差连接中加入一个 $1\times 1$ 卷积,将输入的维度调整回输出的维度,从而保证后续加法的维度一致,如下图所示:
思考:如何通过 1×1 卷积层改变特征图的长度和宽度?
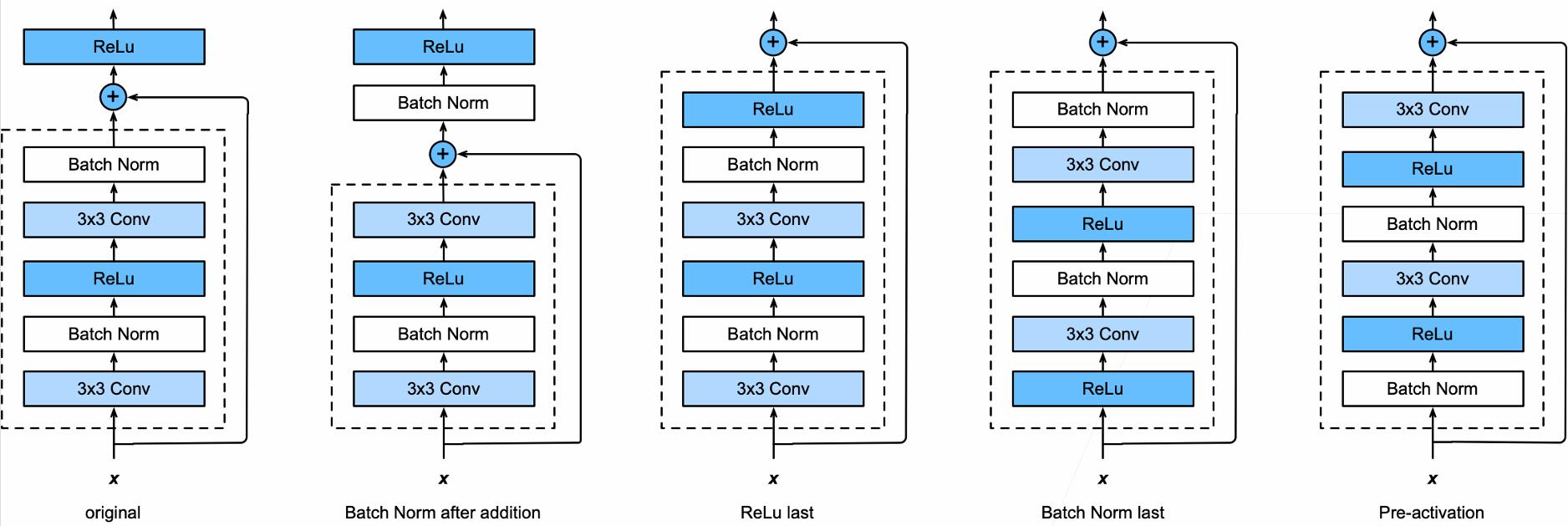
通过设置不同的 stride,比如 stride=2,可以把输入的宽度和高度缩小为原来的 1/2。实际上,ResNet 就是使用了两种 Residual 块:高宽减半的 ResNet 块和 宽高不变的 ResNet 块。有的人可能会问,为什么一定要在第二个卷积层和激活函数之间相加呢?当然可以尝试其他不同的组合,甚至更加多样的残差连接方式,如下图所示:
2.5.2. 反向传播
简单考虑残差块的梯度反向传播:
\[\frac{\partial y}{\partial x} = 1 + \frac{\partial f(x)}{\partial x}\]即使发生了梯度消失:
\[\frac{\partial f(x)}{\partial x}\to 0\quad \Rightarrow \quad \frac{\partial y}{\partial x} = 1\]这保证了梯度至少能无衰减地传递一层。
更一般的情况下,考虑第 $l$ 层的残差块结构:
\[\begin{aligned} y_l &= x_l + \mathcal{F}(x_l,W_l)\\ x_{l+1} &= f(y_l) \end{aligned}\]考虑从输出层 $L$ 层反向传播到第 $l$ 层,根据链式法则:
\[\frac{\partial \mathcal{l}}{\partial x_l} = \frac{\partial \mathcal{L}}{\partial x_L}\frac{\partial x_L}{\partial x_l}\]核心是第二项的展开。对于其中第 $k$ 层($l\leq k< L$)层:
\[\begin{aligned} x_{k+1} &= f(y_{k}) = f(x_k + \mathcal{F}(x_{k},W_{k})) \end{aligned}\]其雅可比矩阵为
\[\begin{aligned} \frac{\partial x_{k+1}}{\partial x_k} &= \frac{\partial f(y_k)}{\partial x_k}\cdot \frac{\partial y_k}{\partial x_k}\\ &=f^\prime (y_k)\cdot (I + \frac{\partial \mathcal{F}(x_{k},W_{k})}{\partial x_k}) \end{aligned}\]那么从 $l$ 到 $L$ 的累计雅可比为
\[\frac{\partial x_L}{\partial x_l} = \prod_{k=l}^{L-1} \frac{\partial x_{k+1}}{\partial x_k} = \prod_{k=l}^{L-1} \left [f^\prime (y_k)\cdot (I + \frac{\partial \mathcal{F}(x_{k},W_{k})}{\partial x_k})\right ]\]定义
\[J_k = \frac{\partial \mathcal{F}(x_k, W_k)}{\partial x_k}\]注意到,$\mathcal{F}$ 通常是几个卷积层,每个卷积层的雅可比模长通常小于 $1$,因此 $J_k$ 通常是一个小值。
使用新定义的 $J_k$ 重新表示累计雅可比,并将连乘展开为多项式形式,有:
\[\begin{aligned} \prod_{k=l}^{L-1} (I + J_k) &= I + \sum_{k=l}^{L-1} J_k + \sum_{l \leq i < j \leq L-1} J_i J_j + \cdots + \prod_{k=l}^{L-1} J_k \end{aligned}\]可以看出,无论多深,ResNet 至少有一个单位矩阵项,且第二项是各层贡献的线性叠加,不会指数衰减。这保证了梯度至少有稳定的回传通路。
如果观察普通的网络(Plain Network),其前后两层的映射关系如下:
\[x_{k+1} = f(\mathcal{F}(x_k,W_k))\]雅可比矩阵为
\[\frac{\partial x_L}{\partial x_l} = \prod_{k=l}^{L-1} \left [ f^\prime (\mathcal{F}(x_k,W_k))\cdot \frac{\partial \mathcal{F}(x_{k},W_{k})}{\partial x_k}\right ]\]其累计雅可比为纯连乘,容易发生梯度消失。
2.5.3. 网络结构
参考 VGGNet 和 GoogLeNet 的总体架构,将其中的结构替换为 ResNet 块,得到 ResNet 的基本框架如下图所示:
ResNet变体:
- ResNet-18:8个残差块(18 个卷积权重层)
- ResNet-34:16个残差块(34 个卷积权重层)
- ResNet-50/101/152:使用 bottleneck 结构(1×1-3×3-1×1)减少计算量
优势:
- 有效缓解深层网络的梯度消失问题
- 使极深网络的训练成为可能
- 残差连接提供了特征复用机制
2.6. 轻量化网络
为适应移动设备等资源受限场景,轻量化网络应运而生:
- MobileNet系列:
- 采用深度可分离卷积(Depthwise Separable Convolution)
- 将标准卷积分解为深度卷积和逐点卷积
- 参数量和计算量显著减少(约为标准卷积的1/8~1/9)
- EfficientNet:
- 提出复合缩放策略(Compound Scaling):统一缩放网络深度、宽度和分辨率
- 基于MobileNetV2的 inverted residual 结构
- 在相同计算资源下性能更优
- ShuffleNet:
- 引入通道混洗(Channel Shuffle)解决分组卷积的通道隔离问题
- 适合移动端部署的高效网络结构