模式识别(线性分类器)
本文介绍了模式识别的线性分类器,包括线性回归、最小二乘估计、Fisher 线性判别分析。
1. 引言
模式识别的目的是在特征空间中设法找到两类(或多类)之间的分界面。一方面,我们可以通过估计样本的概率模型,然后采用贝叶斯决策(最大后验估计)或者最大似然估计的策略来实现分类。但是很多情况下,建立样本的概率模型和准确估计样本的概率密度函数及其他模型参数并不是一件容易的事情。
实际上,估计概率密度函数也不是我们的目的。贝叶斯决策的策略分为两步,首先根据样本进行概率密度函数估计,然后再根据估计的概率密度函数求分类面。如果能直接根据样本求分类面,就可以省略对概率密度函数的估计。我们知道,当样本为正态分布且各类协方差矩阵相等的条件下,贝叶斯决策的最优分类面是线性的,二分类问题的判别函数形式为 $g(x) = \boldsymbol{w}^T\boldsymbol{x} + w_0$。那么如果我们知道判别函数的形式,可以设法从数据中直接估计这种判别函数的参数,这就是基于样本直接进行分类器设计的思想。进一步,即使不知道最优的判别函数是什么形式,仍然可以根据需要或对问题的理解设定判别函数类型,从数据直接求解判别函数。
线性分类器是一种基于样本直接设计的分类器。采用不同的准则及不同的寻优算法就得到不同的线性判别方法。
2. 线性回归与最小二乘估计
多元线性回归是通过 $(\boldsymbol{x},y), \boldsymbol{x}\in \mathbb{R}^d, y\in \mathbb{R}$ 的一系列观测样本,估计他们之间的线性关系
\[y=w_0+w_1x_1+w_2x_2+\cdots+w_dx_d = \sum_{i=0}^d w_ix_i = \boldsymbol{w}^T\boldsymbol{x}\]其中, $\boldsymbol{w} = [w_0, w_1, \cdots, w_d]^T$ 是待定参数。
从机器学习第角度分析线性回归估计,就是用训练样本集估计模型中第参数,使得模型在最小平方误差意义下能够最好地拟合训练样本。即
\[\begin{aligned} \text{sample batch:}\quad & {(\boldsymbol{x}_1, y_1),\cdots, (\boldsymbol{x}_N, y_N)}\\ \text{regression model:}\quad & f(\boldsymbol{x}) = w_0+w_1x_1+w_2x_2+\cdots+w_dx_d = \sum_{i=0}^d w_ix_i = \boldsymbol{w}^T\boldsymbol{x}\\ \text{MSE loss function:}\quad & \min_{\boldsymbol{w}} E = \frac{1}{N}\sum_{j=1}^N(f(\boldsymbol{x}_j)-y_j)^2 \end{aligned}\]目标函数可以写成以下矩阵形式
\[\begin{aligned} E(\boldsymbol{w}) &= \frac{1}{N}\sum_{j=1}^N(f(\boldsymbol{x}_j)-y_j)^2\\ &=\frac{1}{N}\Vert \boldsymbol{X}\boldsymbol{w}-\boldsymbol{y} \Vert^2\\ &=\frac{1}{N}( \boldsymbol{X}\boldsymbol{w}-\boldsymbol{y} )^T ( \boldsymbol{X}\boldsymbol{w}-\boldsymbol{y} ) \end{aligned}\]其中 $\boldsymbol{X}=[\boldsymbol{x}_1^T, \cdots, \boldsymbol{x}_N^T]^T\in \mathbb{R}^{d\times N}$ 是全部训练样本的特征变量组成的矩阵,$\boldsymbol{y}=[y_1, \cdots, y_N]^T$ 是全部训练样本的响应变量(分类标签)组成的向量。
使得上述目标函数最小化的参数 $\boldsymbol{w}$ 应满足
\[\frac{\partial{E(\boldsymbol{w})}}{\partial{\boldsymbol{w}}} = \frac{2}{N}\boldsymbol{X}^T(\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y})=0\]《The Matrix Cookbook》 \(\frac{\partial}{\partial\mathbf{s}}(\mathbf{x}-\mathbf{A}\mathbf{s})^T\mathbf{W}(\mathbf{x}-\mathbf{A}\mathbf{s})=-2\mathbf{A}^T\mathbf{W}(\mathbf{x}-\mathbf{A}\mathbf{s}) \tag{84}\)
那么有
\[\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{w}=\boldsymbol{X}^T\boldsymbol{y}\]当 $\boldsymbol{X}^T\boldsymbol{X}$ 可逆时,最优参数的解为
\[\boldsymbol{w}^{\star}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}\]该方法就是经典的 〖最小二乘法〗 线性回归,其中的矩阵 $(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T$ 被称作 $\boldsymbol{X}$ 的伪逆矩阵(加号逆),记作 $\boldsymbol{X}^+$。
采用上述算法,加入真实的样本是服从之前给出的线性关系的物理规律产生的,只是在观测中带有噪声或误差,则最小二乘线性回归就通过数据学习到了系统本来的模型,而在我们对数据背后的物理模型并不了解的情况下,线性回归给出了在最小平方误差意义下对解释变量与响应变量之间线性关系的最好估计。
3. Fisher 线性判别分析
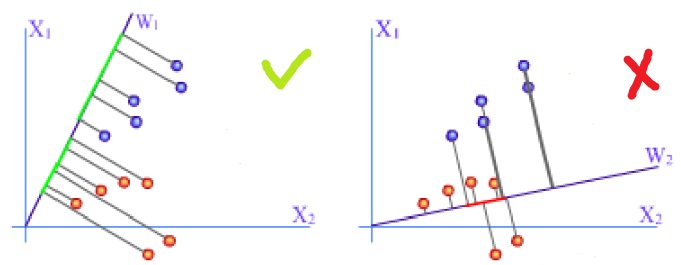
二分类线性判别问题可以看作是把所有样本都投影到一个方向上,然后在这个一维空间中确定一个分类的阈值。过这个阈值点且与投影方向垂直的超平面就是两类的分类面。我们可以从下图中看出,不同的投影方向会使得两类样本的影响该方向的分类结果,左图的投影方向可以使得两类样本较好分开,而按照右图的方向投影后则两类样本混在一起。Fisher 线性判别的思想就是,选择合适的投影方向,使得投影后两类的间隔尽可能远,同时每一类内部的样本又尽可能聚集。
3.1. 投影
假设二维空间的一个特征向量 $\boldsymbol{x}$,某个投影方向向量为 $\boldsymbol{w}$。假设 $\vert \boldsymbol{w} \vert = 1$(因为只关心投影的方向,不关心长度),那么投影向量为
\[\frac{\boldsymbol{w}^T\cdot \boldsymbol{x}}{\vert \boldsymbol{w} \vert} = \boldsymbol{w}^T\boldsymbol{x}\]3.2. Fisher 投影
假设两类样本集,其中第 $w_i$ 类样本集为 $\mathcal{X}i=[\boldsymbol{x}_1^i,\cdots, x{N_i}^i]\in \mathbb{R}^{d\times N_i}$,即特征维度为 $d$,样本个数为 $N_i$。
投影前,原始特征空间中第 $w_i$ 类样本的均值为
\[\boldsymbol{m}_i=\frac{1}{N_i}\sum_{\boldsymbol{x}_j\in \mathcal{X}_i}\boldsymbol{x}_j, \quad i=1,2\]为了度量两类的间隔和每一类内部的聚集程度,可以定义各类的类内离散度矩阵(within-class scatter matrix)为
\[\boldsymbol{S}_i=\sum_{\boldsymbol{x}_j\in \mathcal{X}_i}(\boldsymbol{x}_j-\boldsymbol{m}_i)(\boldsymbol{x}_j-\boldsymbol{m}_i)^T \in \mathbb{R}^{d\times d},\quad i=1,2\]那么总类内离散度矩阵(pooled within-class scatter matrix)为
\[\boldsymbol{S}_w = \boldsymbol{S}_1+\boldsymbol{S}_2\]类间离散度矩阵(between-class scatter matrix)为
\[\boldsymbol{S}_b = (\boldsymbol{m}_1-\boldsymbol{m}_2)(\boldsymbol{m}_1-\boldsymbol{m}_2)^T \in \mathbb{R}^{d\times d}\]将所有样本投影到一维空间,根据前一节的投影公式,投影后的特征向量为
\[y = \boldsymbol{w}^T\boldsymbol{x}\]投影后两类的均值(标量)分别为
\[\tilde{m}_i = \frac{1}{N_i}\sum_{y_j\in \mathcal{Y}_i}y_j=\frac{1}{N_i}\sum_{x_j\in \mathcal{X}_i}\boldsymbol{w}^T\boldsymbol{x}_i = \boldsymbol{w}^T\boldsymbol{m}_i, \quad i=1,2\]投影后的类内离散度和总类内离散度分别为
\[\begin{aligned} \tilde{S}_i &= \sum_{y_j\in \mathcal{Y}_i}(y_j-\tilde{m}_i)^2\\ \tilde{S}_w &= \tilde{S}_1+\tilde{S}_2\\ \end{aligned}\]投影后的类内离散度为
\[\tilde{S}_b = (\tilde{m}_1-\tilde{m}_2)^2\]根据前述 Fisher 投影准则的优化目标(即选择合适的投影方向,使得投影后类间离散度 $S_b$ 尽可能大,同时总类内离散度 $S_w$ 尽可能小)可以写出如下分式形式的优化目标函数:
\[J(\boldsymbol{w}) = \frac{\tilde{S}_b}{\tilde{S}_w}=\frac{(\tilde{m}_1-\tilde{m}_2)^2}{\tilde{S}_1+\tilde{S}_2}\]为了寻找最优投影方向 $\boldsymbol{w}$,需要讲优化目标函数进行改写。由于
\[\begin{aligned} \tilde{S}_b &= (\tilde{m}_1-\tilde{m}_2)^2 \\ &= (\boldsymbol{w}^T\boldsymbol{m}_1-\boldsymbol{w}^T\boldsymbol{m}_2)(\boldsymbol{w}^T\boldsymbol{m}_1-\boldsymbol{w}^T\boldsymbol{m}_2)^T\\ &= \boldsymbol{w}^T(\boldsymbol{m}_1-\boldsymbol{m}_2)(\boldsymbol{m}_1-\boldsymbol{m}_2)^T\boldsymbol{w}\\ &= \boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w} \end{aligned}\]而
\[\begin{aligned} \tilde{S}_w &= \tilde{S}_1+\tilde{S}_2\\ &=\sum_{y_1\in \mathcal{Y}_1}(y_1-\tilde{m}_1)^2+\sum_{y_2\in \mathcal{Y}_2}(y_2-\tilde{m}_2)^2\\ &=\sum_{x_1\in \mathcal{X}_1}(\boldsymbol{w}^T\boldsymbol{x}_1-\boldsymbol{w}^T\boldsymbol{m}_1)^2+\sum_{x_2\in \mathcal{X}_2}(\boldsymbol{w}^T\boldsymbol{x}_2-\boldsymbol{w}^T\boldsymbol{m}_2)^2\\ &=\boldsymbol{w}^T[\sum_{x_1\in \mathcal{X}_1}(\boldsymbol{x}_1-\boldsymbol{m}_1)(\boldsymbol{x}_1-\boldsymbol{m}_1)^T+\sum_{x_2\in \mathcal{X}_2}(\boldsymbol{x}_2-\boldsymbol{m}_2)(\boldsymbol{x}_2-\boldsymbol{m}_2)^T]\boldsymbol{w}\\ &= \boldsymbol{w}^T(\boldsymbol{S}_1+\boldsymbol{S}_2)\boldsymbol{w}\\ &= \boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w} \end{aligned}\]那么优化目标函数可以写成
\[J(\boldsymbol{w}) = \frac{\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}}{\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}}\]上式被称为广义 Rayleigh 商。
从优化目标来看,如果直接对上式(分子分母都是二次型)进行优化,有无穷个满足要求的解。为了解决多解问题,我们需要额外增加一个约束条件,限制解的个数。由于我们只关心投影的方向,对投影方向向量的模长不关心,并且上式分子分母的向量 $\boldsymbol{w}$ 数乘缩放不影响比值。
在我们求导之前,需要对分母进行归一化,因为不做归一的话,$\boldsymbol{w}$ 扩大任何倍,都成立,我们就无法确定 $\boldsymbol{w}$。这里 $\boldsymbol{w}$ 并不是唯一的,倘若 $\boldsymbol{w}$ 对应 $J(\boldsymbol{w})$ 的极大值点,则 $a\cdot \boldsymbol{w}$ 仍旧可以达到 $J(\boldsymbol{w})$ 的极大值点。
因此将优化问题更改如下
\[\begin{aligned} \max &\; \boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}\\ s.t. &\; \boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}=c\neq 0 \end{aligned}\]通过额外引入一个使得分子等于常数的等式约束来限制 $\boldsymbol{w}$ 的取值,然后通过拉格朗日乘子法求解极大值,定义拉格朗日函数如下
\[\begin{aligned} L(\boldsymbol{w},\lambda) &= \boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w} - \lambda (\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}-c)\\ \Rightarrow \frac{\partial L(\boldsymbol{w},\lambda)}{\partial \boldsymbol{w}} &= 2\boldsymbol{S}_b\boldsymbol{w} - 2\lambda \boldsymbol{S}_w\boldsymbol{w}\\ \end{aligned}\]《the Matrix Cookbook》
\[\frac{\partial \boldsymbol{x}^T\boldsymbol{B\boldsymbol{x}}}{\partial \boldsymbol{x}} = (\boldsymbol{B}+\boldsymbol{B}^T)\boldsymbol{x} \tag{81}\]而类间方差矩阵根据其定义,满足 $\boldsymbol{S}_b = \boldsymbol{S}_b^T$,此时有
\[\frac{\partial \boldsymbol{x}^T\boldsymbol{B\boldsymbol{x}}}{\partial \boldsymbol{x}} = 2\boldsymbol{B}\boldsymbol{x}\]
令上式等于零,取到极大值 $\boldsymbol{w}^{\star}$,即
\[\boldsymbol{S}_b\boldsymbol{w}^{\star} = \lambda \boldsymbol{S}_w\boldsymbol{w}^{\star}\]当样本数大于特征维度时,$\boldsymbol{S}_w$ 通常是非奇异矩阵,可求逆,因此有
\[\lambda \boldsymbol{w}^{\star} = \boldsymbol{S}_w^{-1}\boldsymbol{S}_b\boldsymbol{w}^{\star}\]即上述最优化问题倍转化为求矩阵 $\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$ 的特征值 $\lambda$ 和特征向量 $\boldsymbol{w}^{\star}$。
将 $\boldsymbol{S}_b$ 的定义式代入有
\[\lambda \boldsymbol{w}^{\star} = \boldsymbol{S}_w^{-1}(\boldsymbol{m}_1-\boldsymbol{m}_2)(\boldsymbol{m}_1-\boldsymbol{m}_2)^T\boldsymbol{w}^{\star}\]注意到,$(\boldsymbol{m}_1-\boldsymbol{m}_2)^{T}\cdot\boldsymbol{w}^\star$ 是标量,不会改变 $\boldsymbol{w}^ \star$ 的方向,因此可以得到 $\boldsymbol{w}^{\star} $ 是由 $\boldsymbol{S}_w^{-1}(\boldsymbol{m}_1-\boldsymbol{m}_2)$ 决定的,因此 Fisher 投影准则的最优投影方向为
\[\boldsymbol{w}^{\star} = \boldsymbol{S}_w^{-1}(\boldsymbol{m}_1-\boldsymbol{m}_2)\]至此,我们只需要求出原始样本的均值和方差(协方差矩阵?)就可以求出最佳的方向。
需要注意的是,Fisher 投影的最优解本身只给出了一个投影方向,并没有给出我们需要的分类面。要得到分类面,需要再投影后的方向(一维空间)上确定一个分类阈值 $w_0$ 并采取决策规则
\[g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x} + w_0 > 0 \Rightarrow \boldsymbol{x}\in y_1 \\ g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x} + w_0 < 0 \Rightarrow \boldsymbol{x}\in y_2\]