本文介绍了模式识别中特征的概念,包括颜色特征、形状特征、纹理特征、空间关系特征。然后介绍了常用的特征选择与特征提取方法,包括类别可分性准则、最优搜索、次优搜索、启发式搜索、线性特征提取、非线性特征提取等。
1. 特征
模式识别中把每个样本都量化为一组特征来描述,构建特征空间是解决模式识别问题的第一步。
- 「特征」:可以用来体现类别之间相互区别的某些数学测度,也称作属性,测度的值称为特征值。
- 「特征向量」:由被识别的对象(样本)确定一组基本特征,这组特征的取值按向量形式排布,称为该样本的特征向量。
- 「特征空间」:由样本的特征构成的空间,空间的维数就是特征的个数,每个维度就是一个特征,因此每一个样本就是特征空间中的一个点。
通过直接测量得到的特征称为原始特征。原始特征主要包括:物理特征、结构特征、数学特征
- 「物理和结构特征」:一般是由仪器直接测量出来的数值,这类特征易于为人的直觉感知,但是有时难以定量描述,因此不利于机器判别。
- 「数学特征」:则是对仪器所测量数据的进一步计算,比如根据图像中细胞的总光密度、大小、形状、核内纹理等统计特征来区分正常细胞和异常细胞,这类特征易于用机器判别和分析
原始特征是我们直接测量获得的,但往往不能直接用于模式识别中,因为:
- 原始特征不能反应对象的本质特征;
- 原始特征的维度可能很大,不利于分类器设计。
举例:一张大小 $160\times 120$ 的原始卫星图像,如果采用全部灰度值作为特征的话,原始特征即为 19200 维。但如果改为计算卫星的面积、周长、形状、纹理等有效特征,原始特征可能不超过 100 维。
为了设计出更好的分类器,需要对原始特征的测量值集合进行分析,经过选择和变换处理,组成有效的识别特征。处理方式主要包括:
- 特征选择:从原始特征中跳出一组最具有代表性、分类性能好的特征;
- 特征提取:通过映射(或变换)的方法将高维特征映射到低维空间,在低维空间表示样本。
特征选择和特征提取的相似之处在于,二者想要达到的效果一样,即试图去「减少特征数据集中的属性的数目(即特征降维)」。二者的不同在于:
- 特征提取是通过属性组合生成新属性,改变特征空间;
- 特征选择是从原始特征集中选取子集,不更改原特征空间。
1.1. 颜色特征
颜色特征是一种 全局特征,通常对图像或图像区域的方向、大小等变化不敏感,也就是说,颜色特征通常不能很好的描述图像中对象的局部特征。
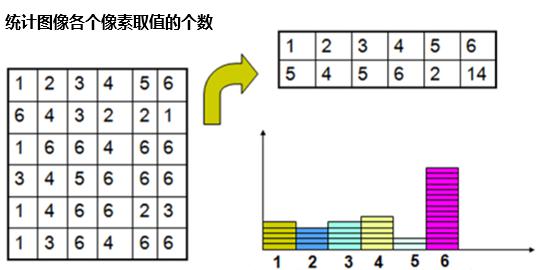
1.1.1. 颜色直方图
颜色直方图描述一幅图像中颜色的全局分布,无法描述图像中颜色的局部分布及每种色彩所处的空间位置,即无法描述图像中的某一具体的对象或物体,只是颜色全局分布的统计结果。因此,颜色直方图只能刻画该范围内像素值的点有多少个,但无法确定点的具体位置。
- 灰度直方图
灰度直方图是由图像中所有像素的灰度级别组成的直方图,它可以用来表示图像中每个灰度级别的像素数量。通常,灰度直方图是一个一维的向量,其长度等于图像的灰度级别数。
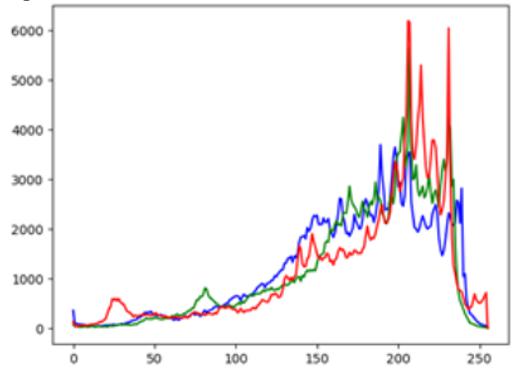
- RGB直方图
当图像为彩色图像时,图像包含 R、G、B 三个通道,可分别统计三个通道颜色取值绘制直方图。
1.1.2. 颜色矩
颜色矩是一种用来描述图像颜色分布的统计特征,主要通过计算图像的颜色一阶矩、二阶矩和三阶矩来反映图像的颜色特征。这些矩分别对应于颜色的「平均值」、「方差」、「偏斜度」、「峰度」,能够有效地表示图像中的颜色分布。由于颜色信息主要分布在低阶矩中,所以用一阶矩、二阶矩、三阶矩和四阶矩足以表达图像的颜色分布。该方法的优点是:不需要颜色空间量化,特征向量维数低;但是该方法的检索效率比较低,实际应用中常用来过滤图像,以缩小检索范围。
- 一阶矩(均值)
一阶矩为原点矩,反应图像的整体明暗程度,值越大越亮。设 $i$ 为图像通道数,$P_{ij}$ 为第 $j$ 个像素在第 $i$ 个通道上的颜色值,则第 $i$ 个通道的一阶矩为:
\[E_i = \frac{1}{N}\sum_{j=1}^{N}P_{ij}\]- 二阶矩(方差)
二阶矩反应图像颜色分布范围,值越大分布越广。第 $i$ 个通道的二阶矩为:
\[\sigma_i = \sqrt[2]{\frac{1}{N}\sum_{j=1}^{N}(P_{ij} - E_i)^2}\]- 三阶矩(偏斜度)
三阶矩反应图像颜色分布的形状(对称性),值为0️零表示图像的颜色分布是对称的,小于零则颜色分布左偏或负偏,大于零则颜色分布右偏或正偏。则第 $i$ 个通道的三阶矩定义为:
\[S_i = \sqrt[3]{\frac{1}{N}\sum_{j=1}^{N}(P_{ij} - E_i)^3}\]- 四阶矩(峰度)
用于描述图像纹理的非线性特性(如尖锐度、尾部权重等),通常与低阶矩结合使用,形成更全面的特征表示。第 $i$ 个通道的四阶矩定义为:
\[M_i = \sqrt[4]{\frac{1}{N}\sum_{i=1}^{N}(P_{ij} - E_i)^4}\]四阶矩常与标准差(二阶矩)结合计算「峰度」(Kurtosis),用于衡量分布尖锐程度:
\[\kappa_i = \frac{M_i - 3}{\sigma_i}\]其中,减 3 是为了使正态分布峰度为 0。峰度量化特性如下:
- 峰度值越小,分布更平坦(轻尾,像素值集中)
- 峰度值越大,分布比正态分布更尖锐(重尾,可能存在异常值)
- 高阶矩能捕捉纹理的微观变化。四阶矩值越高,表明局部像素值变化越剧烈(如高频边缘或复杂纹理)。
- 对抗攻击常导致像素值分布异常,四阶矩可辅助识别人为扰动(相比正常图像,对抗样本的峰度值显著偏离)。
1.2. 形状特征
形状特征描述图像的形状,通常对图像的形状变化敏感,因此,形状特征可以很好的描述图像中对象的 局部特征。
- 轮廓特征:图像形状的外边界;
- 区域特征:面积、周长、半径、长度、宽度、高度。
需要注意的是,形状区域的几何参数提取依赖于图像处理和分割效果,分割质量差可能导致参数无法提取。
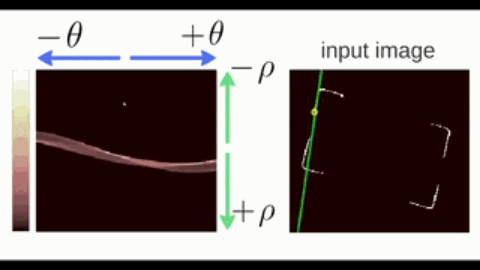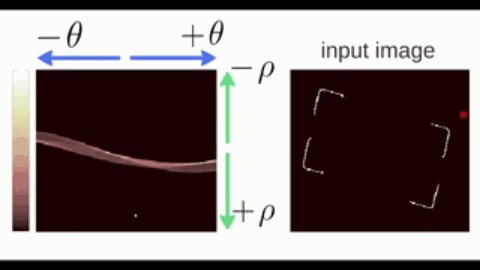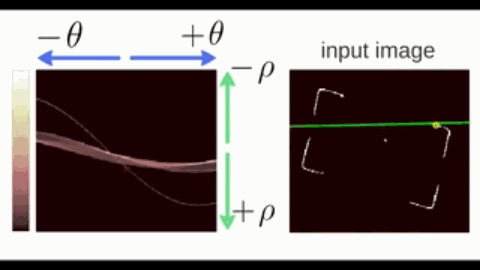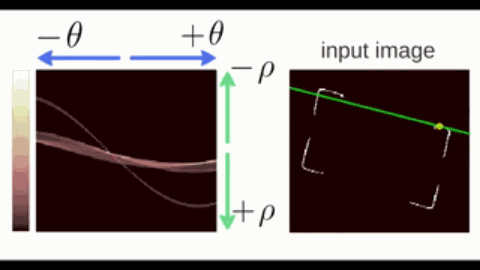
1.2.1. 霍夫变换(Hough)
霍夫变换(Hough Transform)是一种用于检测图像中特定几何形状(如直线、圆、椭圆等)的参数空间投票算法,其核心思想是将图像空间的几何形状映射到参数空间进行累积统计。以直线为例:
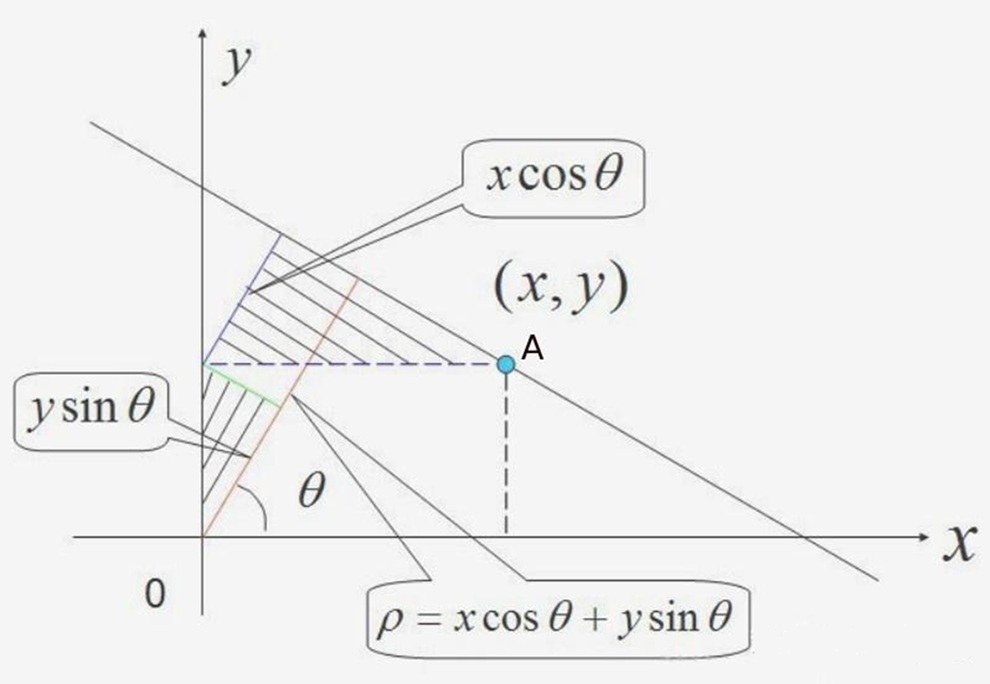
- 在直角坐标系中,直线可以表示为 $y = kx + b$,其中 $a$ 为斜率,$b$ 为截距。但垂直直线($k\to\infty$)会导致参数空间无限大。因此改用极坐标参数化;
- 在极坐标系中,直线可以表示为 $\rho = x \cos \theta + y \sin \theta$,其中 $\theta\in[0,\pi)$ 为直线法线与 $x$ 轴的夹角,$\rho$ 为直线到原点的距离。
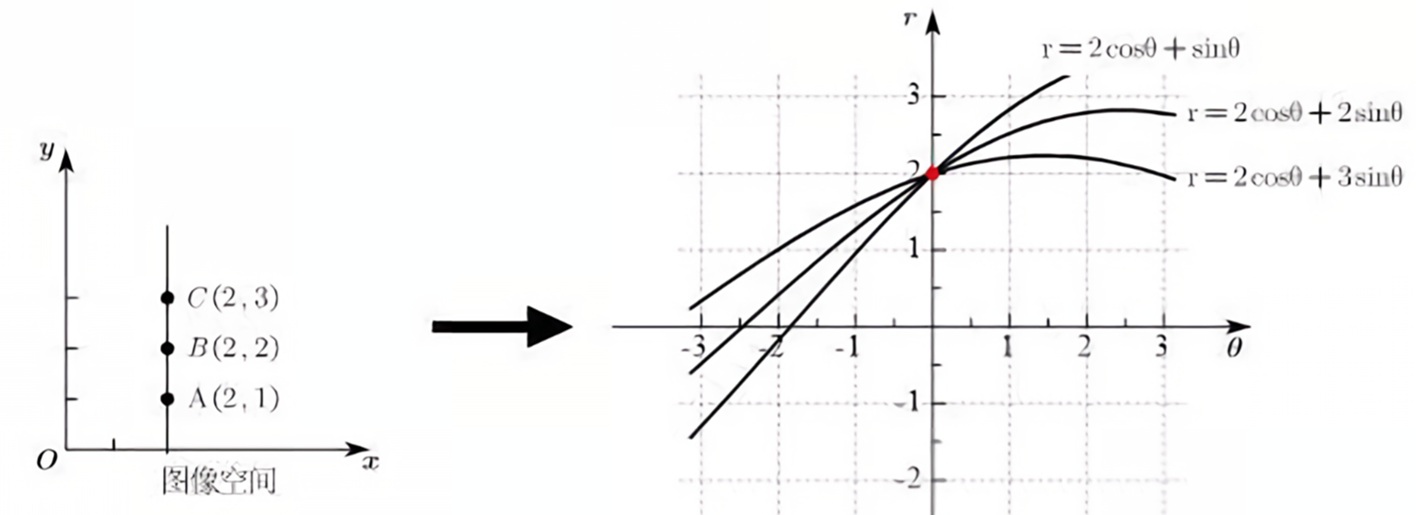
按照极坐标表示,过一个点的所有直线可以在参数空间中绘制出一条 正弦线。
因此,使用 Hough 变换的步骤为:
- 将 $\rho,\theta$ 离散化为若干区间,形成二维累加器数组 $A(\rho,\theta)$ 作为投票矩阵,初始值为0。
- 将图像转为灰度图像,然后使用使用Canny、Sobel等边缘检测算法提取图像中的边缘像素点(得到二值边缘图,边缘点为1,非边缘点为0)
- 对每个边缘点像素使用 Hough 变换,遍历所有可能的 $\theta$ 值,计算对应的 $\rho$ 值;
- 将计算得到的 $(\rho, \theta)$ 四舍五入到最近的离散区间,并在累加器投票矩阵 $A(\rho,\theta)$ 中投票($+1$)。
- 共线的边缘点会在相同的 $(\rho, \theta)$ 处反复投票,形成局部峰值(下图颜色偏白的交点);
- 最后,通过阈值筛选和非极大值抑制,找出若干峰值点,每个峰值点对应图像空间的一条直线。
可参考视频 Hough 变换
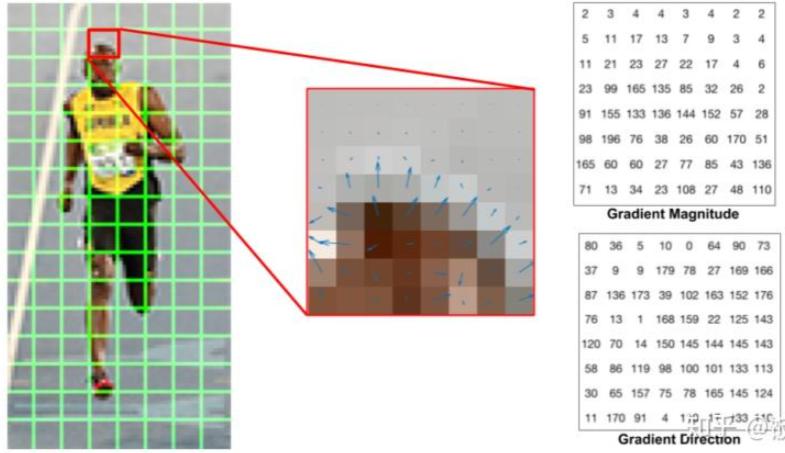
1.2.2. 方向梯度直方图(HOG)
方向梯度直方图(Histogram of Oriented Gradients,HOG)是一种用于图像识别和目标检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来描述图像的边缘特征,特别适用于检测具有明显边缘的目标,如人体、车辆等。HOG 描述子的核心思想是:局部目标的外观和形状可以通过其边缘的方向密度分布来描述。具体步骤如下:
- 对图像进行预处理,将宽高比降低到 $1:2$,如 $64\times 128$;
- 裁剪出若干格子,如 $8\times 8$ 小格,对每个格子的 64 个像素;
- 对于格子中的每个像素,计算其水平梯度$g_x$(右侧像素值-左侧像素值)和垂直梯度 $g_y$(下方像素值-上方像素值);
- 一般采用 Soble 算子卷积,得到 $g_x$ 和 $g_y$;
- 计算该像素的梯度大小 $g = \sqrt{g_x^2 + g_y^2}$;
- 计算该像素的梯度方向 $\theta = \arctan(g_y/g_x)$;
- 按照下面的规则统计格子的梯度直方图:
- 将梯度方向划分为若干区间,如 $0^{\circ},20^{\circ},40^{\circ},\cdots,160^{\circ}$ 共 9 个区间;
- 根据格子中每个像素的梯度方向,将梯度幅值计入对应区间,如梯度方向 $34.3^{\circ}$,幅值 $13.6$:
- 对于 $20^{\circ}$ 区间,累加 $(34.3-20)/20\times 13.6$;
- 对于 $40^{\circ}$ 区间,累加 $(40-34.3)/20\times 13.6$;
- 最终每个小格子得到 9 维向量。
- 通过滑动窗口的形式,将 4 个 $8\times 8$ 格子组成一个块,对块内的直方图进行归一化,以减少光照和阴影的影响。
- 滑动步长为 8 像素,即每次移动 1 个格子,相邻块存在 50% 重叠;
- 每一个块大小为 $16\times 16$,将会得到一个 36 维归一化特征向量。
- 将所有块的归一化直方图特征向量拼接,形成最终的 HOG 特征向量。
- 对于尺寸为 $64\times 128$ 的原始图片,被划分 $(8-1)\times (16-1)=105$ 个块;
- 最终得到 $105 \times 36 = 3780$ 维特征向量,相比原始图片的 $64 \times 128 = 8192$ 维特征向量,HOG 特征向量维度缩小了一半左右。
下面给出了原始图像和其对应 HOG 特征图像的对比,详细计算过程可参考链接 图像特征工程:HOG 特征描述符的介绍。
1.2.3. 傅里叶描述子(Fourier Descriptors)
傅里叶描述子(Fourier Descriptors)是一种用于描述图像形状的特征提取方法,它基于傅立叶变换的原理。傅立叶描述子通过分析形状的轮廓在频域中的表示,能够有效地捕捉形状的特征,并且对形状的平移、旋转和缩放具有一定的不变性。这使得傅立叶描述子在图像识别、目标检测和模式识别等领域中得到了广泛应用。
傅立叶描述子的核心思想是将形状的轮廓表示为一个复数序列,然后对该序列进行傅立叶变换。具体步骤如下:
- 从图像中提取目标的轮廓。轮廓可以表示为一系列的点 $(x_k,y_k)$,其中 $k$ 是点的索引;
- 将轮廓点 $(x_i,y_i)$ 转换为复数序列 $z_k = x_k + iy_k$,其中 $j$ 为虚数单位;
- 对复数序列进行傅立叶变换,得到其频谱 $Z_n=\sum_{k=0}^{N-1}z_k\exp(-i2\pi nk/N)$,其中 $n$ 为频率索引;
- 保留前 $M=10$ 个傅里叶系数,并进行归一化,得到特征向量称为傅里叶描述子。
1.3. 纹理特征
纹理特征也是一种全局特征,指图像中像素的某种空间排列规律,它反映了图像中局部区域的重复性模式或结构。但是,纹理特征不能完全反映出物体的本质属性,仅仅利用纹理特征是无法获得高层次图像内容的。
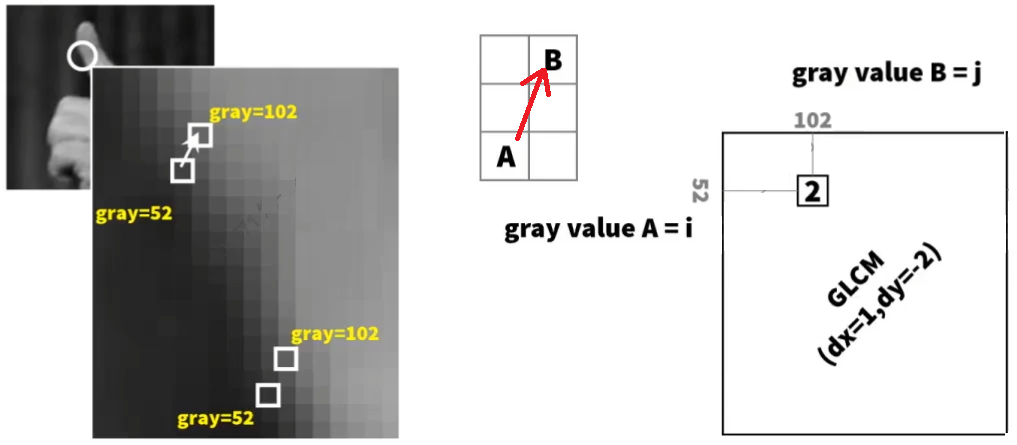
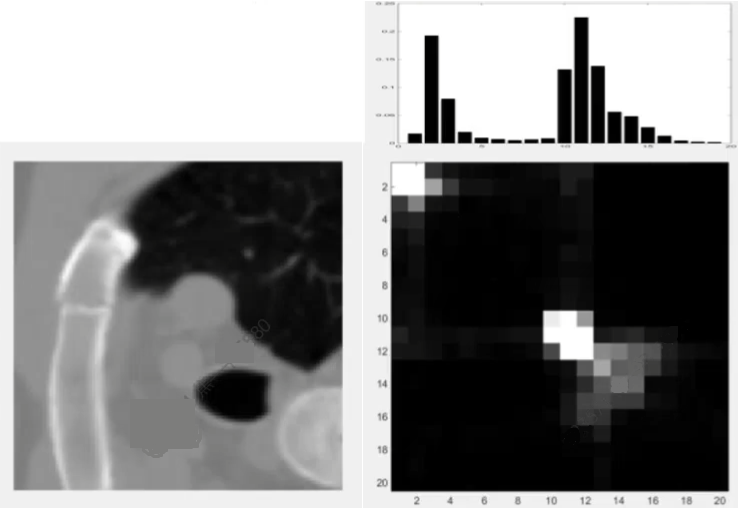
1.3.1. 灰度共生矩阵(GLCM)
灰度共生矩阵(Gray-Level Co-occurrence Matrix, GLCM)是一种用于描述图像中像素对之间灰度值关系的统计方法。它通过计算图像中每对像素在特定方向和距离上的灰度值组合的频率,来提取图像的纹理特征。 GLCM 的计算步骤如下:
- 定义方向和距离
- 选择一个方向 $\theta$(如 $0^{\circ},45^{\circ},90^{\circ},135^{\circ}$)和一个距离 $d$(如 $1,2,3$ 等);
- 方向表示像素对之间的相对位置,距离表示像素对之间的间隔。
- 初始化 GLCM 矩阵
- 创建一个 $N\times N$ 的矩阵,其中 $N$ 是灰度值的数量,用于存储每对像素的灰度值组合的概率 $P(i,j\vert \theta,d)$;
- 将矩阵的每个元素初始化为 0;
- 计算像素对的频率
- 遍历图像中的每个像素,对于每个像素,找到其在指定方向和距离上的邻域像素;
- 增加 GLCM 中对应于当前像素和邻域像素灰度值的元素的值。
- 归一化 GLCM
- 将 GLCM 中的每个元素除以像素对的总数,得到归一化的 GLCM。
- 归一化后的 GLCM 表示了不同灰度值组合的概率分布。
注意,定义方向时一般包含双向信息,比如 $0^{\circ}$ 与 $180^{\circ}$ 是同一方向,而 $45^{\circ}$ 与 $-135^{\circ}$ 是同一方向,因此统计概率时要考虑两种方向的组合。且注意到,灰度共生矩阵在双向定义下一定是一个对称矩阵。
思考:有必要针对原始灰度图像计算灰度共生矩阵么?
- 两不同的灰度像素组合 $51\to 165$ 和 $48\to173$ 几乎无区别!
- 8 位灰度图像的GLCM 尺寸为 $256\times 256 = 65536$ 太大!
- 大量灰度像素组合不存在,概率为 0,GLCM 特别稀疏!
因此,我们可以降低灰度的级别,将其拆成若干区间,如取 $N=8$ 以降低 GLCM 的大小,且有效降低矩阵的稀疏性。
虽然我们从 GLCM 中已经能反映出原图的某些特征,我们一般会将其进一步计算某些统计学特性。
- 对比度
对比度是衡量图像纹理清晰度和纹理粗细程度的指标,反映了图像中像素对之间的灰度差异程度。其计算公式为
\[\text{Contrast} = \sum_{i=1}^{N}\sum_{j=1}^{N}P(i,j\vert \theta,d)|i-j|^2\]对比度值越大,表示图像纹理越清晰,纹理变化越明显,图像中像素对之间的灰度差异越大;对比度值越小,表示图像纹理越模糊,纹理变化越不明显。
- 能量
能量是衡量图像纹理能量和纹理分布均匀度的指标,反映图像纹理的均匀程度。其计算公式为
\[\text{Energy} = \sum_{i=1}^{N}\sum_{j=1}^{N}P(i,j\vert \theta,d)^2\]能量值越大,表示图像纹理分布越均匀,纹理变化越规则(如黑白棋盘);能量值越小,表示图像纹理变化越丰富(如噪声图)。
- 熵
熵是衡量图像纹理混乱程度的指标,反映图像纹理的随机性。其计算公式为
\[\text{Entropy} = -\sum_{i=1}^{N}\sum_{j=1}^{N}P(i,j\vert \theta,d)\log P(i,j\vert \theta,d)\]熵值越大,表示图像纹理分布不均匀,纹理变化越随机;熵值越小,表示图像纹理分布均匀,纹理变化越规则。
越杂乱无序,能量越小,熵越大(熵增、热力学第二定律的体现)。
- 相关性
相关性用于衡量图像中像素对之间的线性相关程度,反映了图像纹理的规则性。其计算公式为
\[\text{Correlation} = \frac{\sum_{i=1}^{N}\sum_{j=1}^{N}(i-\mu_i)(j-\mu_j)P(i,j\vert \theta,d)}{\sigma_i\sigma_j}\]其中
\[\begin{aligned} \mu_i &= \sum_{i=1}^{N}\sum_{j=1}^{N}iP(i,j\vert \theta,d) \\ \mu_j &= \sum_{i=1}^{N}\sum_{j=1}^{N}jP(i,j\vert \theta,d)\\ \sigma_i &= \sqrt{\sum_{i=1}^{N}\sum_{j=1}^{N}(i-\mu_i)^2P(i,j\vert \theta,d)}\\ \sigma_j &= \sqrt{\sum_{i=1}^{N}\sum_{j=1}^{N}(j-\mu_j)^2P(i,j\vert \theta,d)} \end{aligned}\]相关性值通常在 $[−1,1]$ 之间。
- $1$ 表示完全正相关;
- $-1$ 表示完全负相关;
- $0$ 表示无相关性。
高相关性表示图像纹理在指定方向上变化缓慢,低相关性表示纹理变化剧烈。
- 一致性
一致性是用于衡量图像纹理局部变化的大小,即灰度相似的像素对在图像中出现的频率。其计算公式为
\[\text{Homogeneity} = \sum_{i=1}^{N}\sum_{j=1}^{N}\frac{P(i,j\vert \theta,d)}{1+\vert i-j\vert^2}\]一致性值越大,表示图像中灰度相似的像素对越多,图像纹理越均匀;一致性值越小,表示图像中灰度差异较大的像素对越多,图像纹理变化越复杂。
1.3.2. 局部二值模式(LBP)
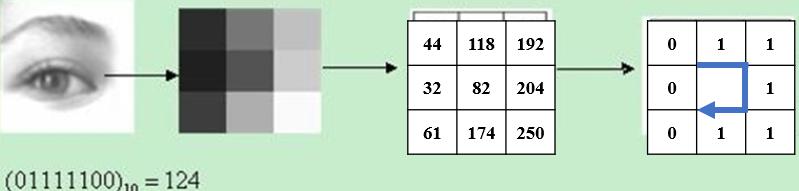
局部二值模式(Local Binary Pattern,LBP)是一种用于描述图像中像素邻域的纹理特征。它通过将图像中每个像素的灰度值与相邻像素的灰度值进行比较,生成一个二进制编码,以表示像素的灰度分布特征。它利用相邻像素间的关系,将0-255灰度级的像素值映射到重新定义的灰度级,然后通过统计直方图来反映图像的全局纹理信息。
如下图所示,在 $3\times 3$ 窗口内,以窗口中心像素为阈值,将相邻 8 个像素的灰度值与其阈值进行比较,得到一个二进制编码。若周围像素值大于中心像素值,则该像素点的位置被标记为 1,否则为 0。$3\times 3$ 邻域内的 8 个点经比较可产生 8 位二进制数(通常转换为十进制数即LBP码,共256种),即得到该窗口中心像素点的LBP值,并用这个值来反映该区域的纹理信息。
经过 LBP 提取后的图像依然是一副图,图片中每个像素记录的就是改像素的 LBP 值(如下图右侧子图所示)。应用中,如纹理分类、人脸分析等,一般都不将 LBP 图谱作为特征向量用于分类识别,而是采用 LBP 特征谱的统计直方图作为特征向量用于分类识别。
LBP 的优点是简单、快速、易于计算、具有灰度不变性,缺点是计算量较大,需要考虑邻域内的像素值,且需要考虑像素的灰度值范围、且不具有旋转不变性。
1.4. 空间关系特征
空间关系是指图像中分割出来的多个目标之间的相互空间位置,或者相对方向关系。包括
- 相对空间位置信息:目标之间的相对情况,如上下左右关系等;
- 绝对空间位置信息:目标之间的距离大小以及方位。
基于空间关系可定义常见的特征如下:
- 连接/邻接关系。
- 交叠/重叠关系。
- 包含/包容关系。
详细介绍略。
2. 特征选择
特征选择的定义为:已知给定的 $M$ 个原始特征。从中优选出 $m$ 个特征($m<M$)。即:从给定的 $M$ 个原始特征中搜索到最优的特征组合。其包含两个方面:
- 选择的标准:定义不同的类别可分离性准则(判据)$J_{ij}$,用来衡量在一组特征下第 $i$ 类和第 $j$ 类之间的可分程度。
- 搜索算法:在允许的时间内找出最优的那组特征。
可分离性准则(判据)应该与错误率(或错误率的上界)有单调关系,这样才能较好地反映分类目标。
当特征独立时,判据对特征应该具有「可加性」。设特征变量为 $x_k,\;k=1,2,\cdots,d$,有
\[J_{ij}(x_1, x_2,\cdots, x_d) = \sum_{k=1}^k J_{ij}(x_k)\]判据应该对特征具有「单调性」,即加入新的特征不会使判据减小
\[J_{ij}(x_1,x_2,\cdots, x_d) \leq J_{ij}(x_1,x_2,\cdots, x_{k-1}, x_{k+1},\cdots, x_d,\textcolor{blue}{x_{d+1}})\]判据还应该具有「以下特性」:
\[J_{ij}\geq 0,\; i\neq j;\quad J_{ij} = 0,\; i=j;\quad J_{ij} = J_{ji}\]2.1. 类别可分性准则
2.1.1. 基于类内类间距离的可分性判据
各类样本可以分开是因为它们位于特征空间中的不同区域,显然这些区域之间距离越大,类别可分性就越大。距离度量有多种,如欧氏距离、各种平均平方距离。假设 $w_i, w_j$ 两个类别中的某两个样本特征向量间的距离定义为:$\delta(\boldsymbol{x}^{(i)}_k,\boldsymbol{x}^{(j)}_l)$,那么基于类内类间距离的可分性判据定义为
\[J_d(\boldsymbol{x}) = \frac{1}{2}\sum_{i=1}^cP_i\sum_{j=1}^cP_j\frac{1}{n_in_j}\sum_{k=1}^{n_i}\sum_{l=1}^{n_j}\delta(\boldsymbol{x}^{(i)}_k,\boldsymbol{x}^{(j)}_l)\]其中,$c$ 为类别数;$n_i,n_j$ 为类 $i$ 和 $j$ 的样本数;$P_i,P_j$ 为类 $i$ 和类 $j$ 的先验概率。
如果我们采用欧氏距离作为距离度量,定义第 $i$ 类的均值为 $\boldsymbol{m}^{(i)}$,则
\[\boldsymbol{m}^{(i)} = \frac{1}{n_i}\sum_{k=1}^{n_i}\boldsymbol{x}^{(i)}_k\]则欧式距离可写为
\[\begin{aligned} \delta(\boldsymbol{x}^{(i)}_k,\boldsymbol{x}^{(j)}_l) =& \Vert\boldsymbol{x}^{(i)}_k-\boldsymbol{x}^{(j)}_l\Vert^2\\ =&\Vert \textcolor{red}{\boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)}}+\textcolor{blue}{\boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)}}+\textcolor{green}{\boldsymbol{m}^{(j)}-\boldsymbol{x}^{(j)}_l}\Vert^2\\ =&\textcolor{red}{\Vert\boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)}}\Vert^2+ \Vert\textcolor{blue}{\boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)}}\Vert^2 + \Vert\textcolor{green}{\boldsymbol{x}^{(j)}_l-\boldsymbol{m}^{(j)}}\Vert^2\\ +& 2(\textcolor{red}{\boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)}})^\top(\textcolor{blue}{\boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)}})\\ +& 2(\textcolor{blue}{\boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)}})^\top(\textcolor{green}{\boldsymbol{x}^{(j)}_l-\boldsymbol{m}^{(j)}})\\ +& 2(\textcolor{red}{\boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)}})^\top(\textcolor{green}{\boldsymbol{x}^{(j)}_l-\boldsymbol{m}^{(j)}}) \end{aligned}\]将上述欧式距离表达式代回可分离性判据定义式,交叉性会相互抵消
对于第一个平方项 $\Vert \boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)} \Vert^2$,代入分离判据后,发现其与 $j,l$ 无关,因此
\[\begin{aligned} &\frac{1}{2}\sum_{i=1}^cP_i\sum_{j=1}^cP_j\frac{1}{n_in_j}\sum_{k=1}^{n_i}\sum_{l=1}^{n_j}\Vert \boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)} \Vert^2\\ = &\frac{1}{2}\sum_{i=1}^cP_i\underbrace{\left(\sum_{j=1}^cP_j\right)}_1\frac{1}{n_in_j}\sum_{k=1}^{n_i}\underbrace{\left(\sum_{l=1}^{n_j}1\right)}_{n_j}\Vert \boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)} \Vert^2\\ = &\frac{1}{2}\sum_{i=1}^cP_i\frac{1}{n_i}\sum_{k=1}^{n_i}\Vert \boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)} \Vert^2\\ \end{aligned}\]对于第三个平方和项 $\Vert \boldsymbol{x}^{(j)}_l-\boldsymbol{m}^{(j)} \Vert^2$,与 $i,k$ 无关,与前述类似
\[\begin{aligned} &\frac{1}{2}\sum_{i=1}^cP_i\sum_{j=1}^cP_j\frac{1}{n_in_j}\sum_{k=1}^{n_i}\sum_{l=1}^{n_j}\Vert \boldsymbol{x}^{(j)}_l-\boldsymbol{m}^{(j)} \Vert^2\\ = &\frac{1}{2}\sum_{j=1}^cP_j\frac{1}{n_j}\sum_{k=1}^{n_i}\Vert \boldsymbol{x}^{(j)}_l-\boldsymbol{m}^{(j)} \Vert^2\\ \end{aligned}\]注意到,上述两项实际上是相同的(只是上下标不同),因此可以合并。
对均值平方和项 $\Vert \boldsymbol{m}^{(i)}_k-\boldsymbol{m}^{(j)} \Vert^2$,其余 $k,l$ 无关,简化后得到
\[\frac{1}{2}\sum_{i=1}^cP_i\sum_{j=1}^cP_j\Vert \boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)} \Vert^2\]对于交叉项,以
\[2(\boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)})^\top(\boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)})\]为例,由于 $\sum_{k=1}^{n_i}(\boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)})=0$(因为所有样本减去其均值的和为零),所以该项为零。同理其它两个交叉项也会因为上述对称性而取零。
可分离性判据进行简化后得到
\[J_d(\boldsymbol{x}) = \sum_{i=1}^cP_i\frac{1}{n_i}\sum_{k=1}^{n_i}\Vert \boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)} \Vert^2 + \frac{1}{2}\sum_{i=1}^cP_i\sum_{j=1}^cP_j\Vert \boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)} \Vert^2\]定义总体均值向量为 $\boldsymbol{m}$,即
\[\boldsymbol{m} = \frac{1}{n}\sum_{i=1}^cP_i\boldsymbol{m}_i\]可以证明,对于第二项(类间散布)有如下两种等价表示
\[\frac{1}{2}\sum_{i=1}^cP_i\sum_{j=1}^cP_j\Vert \boldsymbol{m}^{(i)}-\boldsymbol{m}^{(j)} \Vert^2 = \sum_{i=1}^cP_i\Vert \boldsymbol{m}^{(i)}-\boldsymbol{m} \Vert^2\]可以将左右两边分别展开证明。这个等式在模式识别中非常重要,因为它将全局类间距离(所有类别两两比较)转换为中心距离(各类别与总体均值的距离),简化了计算。
因此最终得到
\[J_d(\boldsymbol{x}) = \sum_{i=1}^cP_i\left[\frac{1}{n_i}\sum_{k=1}^{n_i}\Vert \boldsymbol{x}^{(i)}_k-\boldsymbol{m}^{(i)} \Vert^2 + \Vert \boldsymbol{m}^{(i)}-\boldsymbol{m} \Vert^2\right]\]最终的可分离性判据衡量了类内紧致性和类间分离性的平衡。我们希望选择某些特征 $\boldsymbol{x}^\star$ 使得判据最大,即
\[J(\boldsymbol{x}^\star) = \max_{\boldsymbol{x}} J_d(\boldsymbol{x})\]2.1.2. 基于信息熵的可分性判据
把类别 $w_i,i=1,\cdots,c$ 看作一系列随机事件,它的发生依赖于随机向量𝒙,给定 $x$ 的后验概率 $P(w_i\vert x)$。如果根据 $x$ 能完全确定 $w$,则 $w$ 就没有不确定性,对其本身的观察就不会再提供信息量,此时熵为 0,特征最有利于分类;如果 $x$ 完全不能确定 $w$ ,则𝜔不确定性最大,对本身的观察所提供信息量最大,此时熵为最大,特征最不利于分类。
此时香浓熵定义为
\[H = -\sum_{i=1}^cP(w_i\vert x)\log_2 P(w_i\vert x)\]平方熵(基尼系数)定义为
\[H = 2[1-\sum_{i=1}^cP(w_i\vert x)^2]\]在熵的基础上,对特征的所有取值积分,就得到基于信息熵的可分性判据
\[J_E = \int H(\boldsymbol{x})p(\boldsymbol{x})\text{d}x\]最后希望最小化该判据,判据越小可分性越好。
2.2. 最优搜索
理想的特征选择方法可以从给定的 $M$ 个原始特征中根据前述最优性判据,选出 $m\leq M$ 个特征,使得判据最小。如果使用全局搜索,搜索次数为
\[C_M^m = \frac{M!}{(M-m)!m!}\]为了减小搜索次数,采用分支定界算法(Branch and Bound,B&B),算法将所有可能的组合构成一个树状结构,按照特定的规则对树进行搜索和回溯,尽早达到最优解,而不必遍历树的所有分支。
注意,分支定界法使用的前提是最优性判据必须满足单调性。
分支定界法常在运筹学的整数线性规划中被介绍。
2.3. 次优搜索
即使采用 B&B 方法的计算量在有些情况下仍然难以接受。此时,一般会放弃最优搜索,转而使用计算量更小的次优搜索。
2.3.1. 单独最优特征组合
对所有 $M$ 个特征分别单独计算类别可分性判据,然后对单个特征的判据取值进行排序,选择其中前 $m$ 个单独最优的特征进行组合。
这个方法有个前提,即假设单独使用时性能最优的特征,组合起来也是性能最优的。显然,在实际情况中这种假设不一定成立,即使特征是相互独立的,单独最优的特征组合也不一定是最优的。只有当判据是每个特征的判据的和或者积时,才能得到最优特征。
2.3.2. 顺序后向搜索
顺序后向搜索(Sequential Backward Selection, SBS)是一种贪心搜索算法,属于封装式(Wrapper)特征选择方法,通过逐步剔除最不重要的特征来优化模型性能。与顺序前向搜索(SFS)相反,SBS从完整特征集开始,每次删除一个对模型贡献最小的特征,直到达到目标特征数。
显然,上述过程也是一个次优搜索过程,因为最终得到的最优特征组合,其上一步的来源并不一定是最优的特征组合。
案例:基于SBS的乳腺癌分类(Wisconsin数据集)
- 数据:30个特征,目标预测肿瘤良恶性。
- 模型:SVM分类器,评估函数为5折交叉验证准确率。
- SBS过程:
- 初始:30个特征,准确率 $95\%$;
- 迭代剔除最不重要特征,每次保留使准确率下降最少的子集(此时判据直接选用分类准确率);
- 终止:10个特征,准确率 $94.5\%$(几乎无损失,但特征数减少2/3)。
2.3.3. 顺序前向搜索
顺序前向搜索(Sequential Forward Selection, SFS)是一种贪心搜索算法,属于封装式(Wrapper)特征选择方法。它从空特征集开始,逐步添加对模型性能提升最大的单个特征,直到达到目标特征数或性能不再显著提高。与后向搜索(SBS)相反,SFS适用于特征数较多的场景,计算效率更高。
案例:基于SFS的文本分类(TF-IDF特征)
- 数据:10,000 个 TF-IDF 特征(词汇表),目标为新闻分类。
- 模型:逻辑回归,评估函数为 5 折交叉验证 $F1$ 分数。
- SFS过程:
- 初始:0 个特征,$F1=0$。
- 迭代添加使 $F1$ 提升最大的词。
- 终止:100 个特征,$F1=0.89$(接近全特征集的 $0.90$,但特征数减少 $99\%$)。
2.3.4. 浮动搜索
不论是顺序后向搜索还是顺序前向搜索,它们都存在一个弊端:
- 对于顺序后向搜索,某一个特征一旦被去掉就不会再被选中;
- 对于顺序前向搜索,某一个特征一旦被选中就不会再被去掉。
他们都是根据局部最优准则来选取或去除特征的,很可能无法得到最优的特征组合。一种简单的改进思路就是将这两种方法结合起来,在去除或者选择过程中引入一个回溯步骤,允许被选择或者去除的特征正可以被重新选择或去除,这种技术被称为浮动搜索技术。
- 对于顺序后向搜索,若剔除某特征后性能下降过大,可在后续迭代中重新加入;
- 对于顺序前向搜索,若选择某特征后性能下降,可在后续迭代中重新去除。
2.4. 启发式搜索
2.4.1. 遗传算法
遗传算法(Genetic Algorithm,GA)把候选对象编码为一条染色体(chromesome),在特征选择中,如果目标是从 $D$ 个特征中选择 $d$ 个,则把所有特征描述为一条由 $D$ 个二进制数($0/1$)组成的字符串,$0$ 代表该特征没有被选中,$1$ 代表该特征被选中,这个字符串就叫做染色体,记作 $m$。显然,要求的是一条有且仅有 $d$ 个 $1$ 的染色体,这样的染色体共有 $C_8^4$ 种。 优化的目标被描述成适应度(fitness)函数,每一条染色体对应一个适应 度值 $f(m)$。可以用前面定义的两种类别可分性判据为适应度。
使用遗传算法寻找最优特征组合的具体步骤如下:
- 初始化:
- $t=0$
- 设定种群规模 $k$,随机初始化 $k$ 条染色体 $m_1, m_2, …, m_k$,形成初代种群 $M(t)$;
- 初始化交叉率、变异率、迭代次数;
- 遗传操作:
- 计算各个染色体的适应度 $f(m_i),\;i = 1, 2, …, k$;
- 选择
- $t = t + 1$
- 根据适应度值,选择一部分染色体作为父染色体,组成初始的下一代种群 $M(t)$;
- 按照染色体的适应度值逐个累加形成一个区间,然后从 $[0,1]$ 区间随机选择一个数,该数落在那个区间就取哪条染色体;
- 这样保证适应度高的父染色体被选择的概率高;
- 交叉
- 遍历每两个随机染色体,根据交叉率判断是否进行交叉;
- 若是,从第一个父染色体中随机选取一个长度为 $l$ 的片段,记录其中值为 $1$ 的基因个数;
- 从第二个父染色体中寻找长度相同且与前述基因值为 $1$ 的个数相同的片段,若找到则进行交叉操作,反之则再选择一个父染色体直到遍历整个父代种群;
- 变异
- 遍历每一个染色体,按变异率确定是否进行变异操作;
- 若是,随机地选择一个基因进行反转,若该基因由 $1$ 变为了 $0$, 则再随机选一个 $0$ 变成 $1$。
- 迭代:
- 得到最终的下一代种群 $M(t)$;
- 若满足迭代次数则停止迭代,输出种群中适应度最大的染色体作为特征选择结果;
- 否则返回遗传操作,继续迭代。
2.4.2. 模拟退火算法
模拟退火算法(Simulated Annealing,SA)来源于固体退火原理,是一种基于概率的算法。算法思想为:先从一个较高的初始温度出发,逐渐降低温度,直到温度降低到满足热平衡条件为止。在每个温度下,进行 $n$ 轮搜索,每轮搜索时对旧解添加随机扰动生成新解,并按一定规则接受新解。
使用模拟退火算法寻找最优特征组合的具体步骤如下:
- 初始化:
- $t=0$
- 随机产生一个解 $m(t) = [0 1 1 0 0 1 0 \cdots]$;
- 设定初始温度 $T = 1000$,设定退火系数 $\alpha = 0.9$,设定退火迭代次数 $N = 1000$;
- 在当前温度迭代:
- 计算当前温度 $T = T \times \alpha$;
- 遍历 $N$ 次:
- 计算解 $m(t)$ 的适应度 $f(m(t))$;
- 对解进行随机扰动,如选取相异的某两位翻转 $m(t^\prime) = [0 \textcolor{red}{0} 1 0 0 1 \textcolor{red}{1} \cdots]$;
- 计算扰动后解 $m(t^\prime)$ 的适应度 $f(m(t^\prime))$;
- 计算扰动前后评价函数的差值 $\Delta = f(m(t^\prime)) - f(m(t))$,假设要求评价函数越小越好;
- 若 $\Delta < 0$,则接受扰动后的解 $m(t^\prime)$ 作为新解;
- 若 $\Delta \geq 0$,则根据一定概率接受扰动后的解 $m(t^\prime)$ 作为新解;
- 概率函数为:$P=\exp(\frac{-\Delta}{T})$,此处参考多磁体系统或合金中多原子系统达到最低能量的退火方法;
- $t = t^\prime$
3. 特征提取
3.1. 线性特征提取
3.1.1. 线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis,LDA)是一类有监督的线性特征提取算法,它的目的是选取一组最优投影方向,是的投影之后的同类样本尽可能靠近,不同类样本尽可能远离。
LDA 已经在 前述章节 (模式识别 - LDA&PCA - 线性判别分析)中进行了详细介绍,此处不再赘述。
3.1.2. 主成分分析(PCA)
主成分分析(Principal Component Analysis,PCA)是常用的特征提取数据分析方法。PCA是通过线性变换,将原始数据变换为一组各维度线性无关的数据表示方法,可用于提取数据的主要特征分量,常用于高维数据的降维。
PCA 已经在 前述章节 (模式识别 - LDA&PCA - 主成分分析)中进行了详细介绍,此处不再赘述。
3.2. 非线性特征提取
3.2.1. 核方法
核方法(Kernel Method)是机器学习中一种非线性特征提取方法,它利用核函数将原始数据映射到高维空间,从而实现非线性特征提取。
常用的核函数有线性核、多项式核、高斯核、拉普拉斯核以及 Sigmoid 核等。常见的用于非线性特征提取的核方法有核 Fisher 线性判别分析(KFDA)、核主成分分析(KPCA)等。
关于核的详细介绍请参考 前述章节(模式识别 - 非线性分类器 - 核技巧)。
3.2.2. 流形学习
由于传统的线性特征提取算法(PCA、LDA)以及核方法都是试图发现数据的全局结构,对于原始空间中数据可能存在的局部信息或者低维流形结构没有给予关注,而流行学习(Manifold Learning)是基于局部性质的,旨在发现高维数据的分布规律,揭示其内在几何结构。
- 流形与流形学习
流形是局部具有欧几里得空间性质的拓扑空间。换句话说,流形是一个可以在局部范围内近似为欧几里得空间的空间。换言之,它在局部空间有欧式空间的性质,能用欧式空间来进行距离计算。因此,很容易地在局部建立降维映射关系,然后再设法将局部关系推广到全局,进而进行可视化展示。
更加严谨地说,流形是在局部与欧氏空间同胚的空间。换言之,它在局部具有欧氏空间的性质,能用欧氏距离来进行距离计算。流形是欧几里得空间中的曲线、曲面等概念的推广。
例:地球表面就是一个二维流形的例子。尽管地球表面是一个三维空间的曲面,但是在局部范围内,地球表面看起来是平坦的(三维$\to$二维)。意味着在小的区域内,我们可以使用二维坐标系(如纬度和经度)来描述地球表面上的点。
流形学习认为,我们所能观察到的数据实际上是由一个低维流形映射到高维空间的。由于数据内部特征的限制,一些高维中的数据会产生维度上的冗余,实际上这些数据只要比较低的维度就能唯一的表示。
若低维流形嵌入到高维空间中,则数据样本在高维空间的分布虽然看上去非常复杂,但在局部上仍具有欧氏空间的性质,因此,可以容易地在局部建立降维映射关系,然后再设法将局部映射关系推广到全局。
当维数被降至二维或三维时,能对数据进行可视化展示,因此流形学习也可被用于可视化。
流形学习在处理非线性数据结构时特别有效,它能够揭示数据背后的复杂关系,而不仅仅是通过线性变换来简化数据。
流形学习的基本表述如下:
设 $\boldsymbol{Y} \in \mathbb{R}^d$ 是一个低维流形,映射 $f:\boldsymbol{Y}\to \mathbb{R}^D$ 是一个光滑嵌入,其中 $D>d$ 是高维空间。假设经过 $f$ 映射为观察空间的数据为 $\boldsymbol{x}_i=f(\boldsymbol{y_i})$,流形学习就是在给定 $\boldsymbol{x}_i$ 的条件下,重构 $f$ 和 $\boldsymbol{y}_i$。
- 多维多尺度变换(Multi-Dimensional Scaling,MDS)
该方法的核心思想:找到一个低维空间使得样本间的距离在高维空间和低维空间基本一致,即约简后低维空间中任意两点间的距离应该与它们在原高维空间中的距离相同。所以 MDS 算法是利用样本间的相似性来保持降维后的使用效果与降维前一致。
一般情况下,在低维空间可以使用欧氏距离度量样本间的相似关系,MDS 方法将其推广到高维空间,在高维空间中也采用欧氏距离度量样本间的距离。但是,直接在高维空间中计算欧式距离具有误导性,因为高维空间中的直线距离在低维嵌入流形上不可达。而低维嵌入流形上两点间的本真距离是 测地距离(geodesic distance)。
两点之间的测地距离的计算,可以利用流形在局部上与欧式空间同胚这个性质,对于每个点基于欧式距离找出其最近邻点,然后就能建立一个近邻连接图,于是计算两点之间的测地距离的问题,就转变成为计算近邻连接图上两点之间的最短路径问题(Dijkstra算法)。
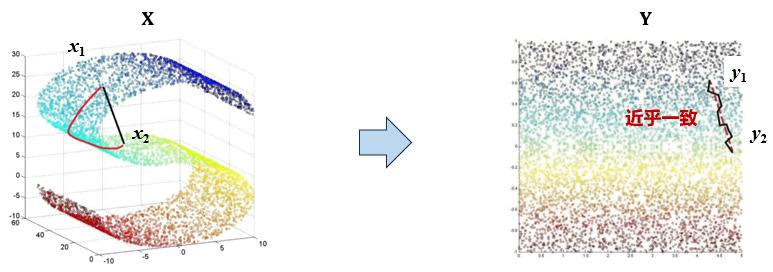
- 等度量映射(Isometric Mapping,Isomap)
Isomap 方法对 MDS 方法进行了改进,通过保持数据点之间的测地距离来保留流形结构。它利用数据点之间的近邻关系建立一个连接图,并计算出数据点在流形上的近似测地距离,然后将数据映射到一个更低维空间,在此低维空间中的欧式距离和高维空间近似测地距离保持近乎一致。
Isomap 的算法伪代码如下:
以 Isomap 论文(A Global GEometric Framework for Nonlinear Dimensionality Reduction)中的原始例子为例,给出的数据集是 698 个 $64\times 64$ 的同一个人的脸部图像,那么每一个图像就相当于 4096 空间中的一个坐标点,实际上这些人脸照片也是嵌入在一个流行体内,根据主观判断,我们可以得出影响人脸的因素有三个:光照方向、是否上下抬头、是否左右偏头。使用 Isomap 将数据降维到二维空间可得
- 横坐标:人左右偏头的程度;
- 纵坐标:人上下偏头的程度
- 滑动条:光照的方向。
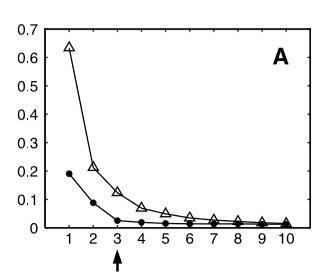
下图给出了 Isomap 和 PCA 降维后的残差对比。图中纵轴是残差方差,其值越小表示和原始数据越相近。横轴表示降维之后的特征维度。
其中空心三角是PCA对人脸图片降维的残差方差,实心圆圈是 Isomap 对人脸图片进行降维的残差方差。可以看出 Isomap 效果要优于 PCA。观察代表isomap的曲线,当维度等于 3 的时候,方差残差下降非常快,同时在维度高于 3 之后,残差方差值变化很小。我们可以断定流行体是三维的数据点嵌入到了高维空间。
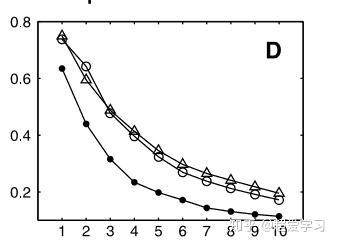
另一个例子是 MNIST 手写数字识别的案例,数据集一共有 1000 个数据项,每个数据项是 $28\times 28$ 大小的图片。将数据降维至 2 维,我们通过观察低维空间数据点代表的图像,发现有两个明显的特征:
- 横坐标表示数字 2 底部是否有一个环形;
- 纵坐标表示数字 2 顶部的歪曲角度的大小。
与 PCA 方法的残差对比曲线如下图所示。
- 局部线性嵌入(Local Linear Embedding,LLE)
lsomap 算法是全局的,它要找到所有样本的全局最优解,当数据量很大时或者样本维度很高时,计算量非常大。因此更常用的算法是局部线性嵌入,LLE 放弃所有样本全局最优的降维,只是通过保证局部最优来降维。LLE 算法的两个基本假设是:
- 一个流形的局部可以近似于一个欧式空间;
- 每个样本都可以利用其邻居进行线性重构。
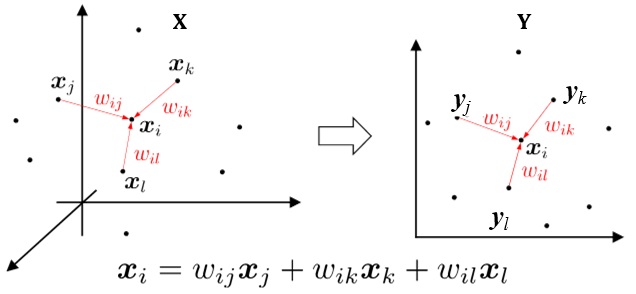
因此,LLE 算法通过构造样本点和它的邻域点之间的权向量,并在低维空间保持每个邻域中的权值不变来实现降维。如下图所示
LLE 算法的过程如下:
- 设高维空间 $\mathbb{R}^D$ 中给定样本集 $\boldsymbol{X}=[\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_N],\boldsymbol{x}_i\in\mathbb{R}^{D\times 1}$,投影之后的低维流形 中的特征样本集为 $\boldsymbol{Y} = [\boldsymbol{y}_1,\boldsymbol{y}_2,\dots,\boldsymbol{y}_N]$;
-
求取每个特征样本的 $k$ 个邻域点,构成邻域集 $\boldsymbol{X}_i$
\[\boldsymbol{X}_i = [\boldsymbol{x}_{i}^{(1)},\boldsymbol{x}_{i}^{(2)},\dots,\boldsymbol{x}_{i}^{(k)}]\in\mathbb{R}^{D\times k}\] -
求取该特征样本与它的各个邻域点之间的权向量 $w_{ij}$,使得该特征样本用它的近邻点线性表示的「均方误差」最小。
为了保证解的唯一性,对权向量添加一个正则化约束,则基于均方误差来优化权向量的优化问题可表示为
\[\min_{\boldsymbol{w}_i} \frac{1}{2}\Vert \boldsymbol{x}_i - \sum_{j=1}^k w_{ij} \boldsymbol{x}_{i}^{(j)} \Vert^2\quad s.t. \sum_{j=1}^k w_{ij} = 1\]注意到,权重的优化求解是逐点独立进行的,而不是对所有样本的权重联合优化。这是LLE的核心思想之一:局部线性重构。
令
\[\boldsymbol{w}_i = [w_{i1},w_{i2},\dots,w_{ik}]^\top\in\mathbb{R}^{k\times 1}\]对目标函数变形如下
\[\begin{aligned} J(\boldsymbol{w}_i) &= \frac{1}{2} \Vert \boldsymbol{x}_i - \sum_{j=1}^k w_{ij} \boldsymbol{x}_{i}^{(j)} \Vert^2\\ &=\frac{1}{2} \Vert \boldsymbol{x}_i - \boldsymbol{X}_{i}\boldsymbol{w}_i \Vert^2\\ &= \frac{1}{2} (\boldsymbol{x}_i - \boldsymbol{X}_{i}\boldsymbol{w}_i)^\top (\boldsymbol{x}_i - \boldsymbol{X}_{i}\boldsymbol{w}_i)\\ &= \frac{1}{2} (\boldsymbol{x}_i^\top\boldsymbol{x}_i-\boldsymbol{x}_i^\top\boldsymbol{X}_{i}\boldsymbol{w}_i -\boldsymbol{w}_i^\top\boldsymbol{X}_i^\top\boldsymbol{x}_i + \boldsymbol{w}_i^\top\boldsymbol{X}_{i}^\top\boldsymbol{X}_{i}\boldsymbol{w}_i)\\ \end{aligned}\]考虑到目标函数中,第一项是常数项,不影响优化,可忽略;第二项和第三项都是标量,转置等于自身,可合并。最终有
\[J(\boldsymbol{w}_i) = \frac{1}{2} \boldsymbol{w}_i^\top\boldsymbol{X}_{i}^\top\boldsymbol{X}_{i}\boldsymbol{w}_i - \boldsymbol{w}_i^\top\boldsymbol{X}_{i}^\top\boldsymbol{x}_i\]对约束条件同样进行矩阵化,有
\[\sum_{j=1}^k w_{ij} = 1 \Rightarrow \boldsymbol{w}_i^\top\cdot \boldsymbol{1}_{k\times 1}=1\]上述问题可采用拉格朗日乘子法求解
\[L(\boldsymbol{w}_i) =\frac{1}{2} \boldsymbol{w}_i^\top\boldsymbol{X}_{i}^\top\boldsymbol{X}_{i}\boldsymbol{w}_i - \boldsymbol{w}_i^\top\boldsymbol{X}_{i}^\top\boldsymbol{x}_i + \lambda \left(\boldsymbol{w}_i^\top\cdot \boldsymbol{1}_{k\times 1}-1\right)\]对 $\boldsymbol{w}_i,\lambda$ 求导并令导数等于零可得到
\[\begin{cases} \boldsymbol{X}_i^\top \boldsymbol{X}_i \boldsymbol{w}_{i} - \boldsymbol{X}_i^\top\boldsymbol{x}_i + \lambda \boldsymbol{1}_{k\times 1} = 0\\ \boldsymbol{w}_i^\top \cdot \boldsymbol{1}_{k\times 1} - 1 = 0 \end{cases}\]解方程组,令 $\boldsymbol{C}=\boldsymbol{X}_i^\top \boldsymbol{X}_i$,有
\[\boldsymbol{w}_i^\star = \frac{\boldsymbol{C}^{-1}\boldsymbol{1}_{k\times 1}}{\boldsymbol{1}_{k\times 1}^\top \boldsymbol{C}^{-1}\boldsymbol{1}_{k\times 1}}\] -
映射到低维流形 $\mathbb{R}^d$ 后,保持权向量不变,求 $\boldsymbol{x}_i$ 在低维空间的映射 $\boldsymbol{y}_i\in\mathbb{R}^{d\times 1}$,使得低维重构误差最小。
同时,上述优化问题还需要满足,低维特征的每个维度均值为 0, 方差为 1。因此,针对低维映射的优化问题可表示为
\[\begin{aligned} \min_Y& \sum_{i=1}^N \Vert \boldsymbol{y}_i - \sum_{j=1}^k w_{ij} \boldsymbol{y}_i^{(j)} \Vert_2^2\\ s.t.& \sum_{i=1}^N \boldsymbol{y}_i = 0, \frac{1}{N}\sum_{i=1}^N \boldsymbol{y}_{i}\boldsymbol{y}_{i}^\top = \boldsymbol{I} \end{aligned}\]其中 $\boldsymbol{y}_i^{(j)}$ 是 $\boldsymbol{y}_i$ 的近邻点,对应高维空间中 $\boldsymbol{x}_i^{(j)}$ 的低维映射。
将目标函数改写为矩阵形式,有
\[\begin{aligned} J(Y) &= \Vert \boldsymbol{Y}-\boldsymbol{Y}\boldsymbol{w}_i^\star \Vert^2_F\\ &= \text{tr}[(\boldsymbol{Y}-\boldsymbol{Y}\boldsymbol{w}_i^\star)^\top(\boldsymbol{Y}-\boldsymbol{Y}\boldsymbol{w}_i^\star)]\\ &=\text{tr}[\boldsymbol{Y}^\top(\boldsymbol{I}-\boldsymbol{w}_i^\star)^\top(\boldsymbol{I}-\boldsymbol{w}_i^\star)\boldsymbol{Y}] \end{aligned}\]定义矩阵 $\boldsymbol{M} = (\boldsymbol{I}-\boldsymbol{w}_i^\star)^\top(\boldsymbol{I}-\boldsymbol{w}_i^\star)$,则问题转化为
\[\min_Y \;\text{tr}(\boldsymbol{Y}^\top\boldsymbol{M}\boldsymbol{Y})\quad s.t. \quad\boldsymbol{Y}\boldsymbol{Y}^\top = N\boldsymbol{I},\quad \sum_{i=1}^N \boldsymbol{y}_i = 0\]优化问题等价于求解矩阵 $\boldsymbol{M}$ 的最小的 $d$ 个特征值对应的特征向量(需要排除零特征值),这可以通过拉格朗日乘子法进行求解展开得到验证。需要对 $\boldsymbol{M}$ 进行特征分解。
4. 参考文献
- Cat food. 形象理解拉格朗日乘子法