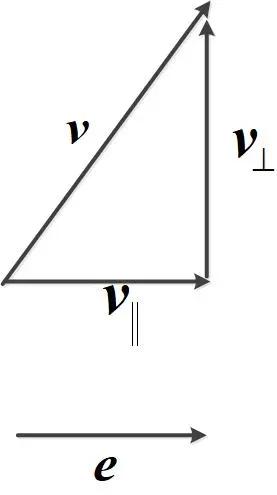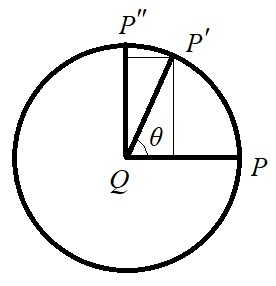本文介绍了航天器姿态描述、姿态变换和姿态运动学中涉及的四元数表示法。
1. 基础
1.1. 矢量的正交分解
对一个矢量 $\boldsymbol{v}$ 进行沿单位参考轴 $\boldsymbol{e}$ 正交分解为两个分量,分别为平行于 $\boldsymbol{e}$ 的轴向分量和垂直于 $\boldsymbol{e}$ 的垂直分量。如下图所示。
有
\[\begin{aligned} \boldsymbol{v}_{\parallel} &= (\boldsymbol{e}^\top\boldsymbol{v})\boldsymbol{e} = \boldsymbol{e}\boldsymbol{e}^\top\boldsymbol{v}\\ \boldsymbol{v}_{\perp} &= \boldsymbol{v} - \boldsymbol{v}_{\parallel} = (\boldsymbol{I} - \boldsymbol{e}\boldsymbol{e}^\top)\boldsymbol{v}\\ \end{aligned}\]若平面 $\boldsymbol{\pi}$ 的法向量为 $\boldsymbol{e}$,那么矢量 $\boldsymbol{v}$ 在平面上的投影矢量 $\boldsymbol{v}^\prime$ 即为
\[\boldsymbol{v}^\prime = \boldsymbol{v}_{\perp} = (\boldsymbol{I} - \boldsymbol{e}\boldsymbol{e}^\top)\boldsymbol{v}\]从而正交投影变化矩阵为
\[\boldsymbol{R} = \boldsymbol{I}-\boldsymbol{e}\boldsymbol{e}^\top\]1.2. 叉乘矩阵
设 $\boldsymbol{a} = [a_1,a_2,a_3]^\top\in\mathbb{R}^3,\; \boldsymbol{b} = [b_1,b_2,b_3]^\top\in\mathbb{R}^3$,那么向量 $\boldsymbol{a}$ 叉乘向量 $\boldsymbol{b}$ 可表示为
\[\boldsymbol{a}\times\boldsymbol{b} = \boldsymbol{a}^\times\boldsymbol{b}\]其中叉乘矩阵满足
\[\boldsymbol{a}^\times = \frac{\partial(\boldsymbol{a}\times\boldsymbol{b})}{\partial \boldsymbol{b}} = \begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{bmatrix}\]七绝一首,速求法向量 向量横着写两遍, 掐头去尾留中间, 交叉相乘再相减, 求得向量再化简。 或者写成行列式方便记忆 \(\left | \begin{matrix} i & j & k\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ \end{matrix} \right |\)
1.3. 坐标系定义
在航天器相对位姿跟踪任务中,需要明确各个坐标系,并以此来描述刚体的位姿和受力情况。通常会涉及到以下几个相关坐标系。
- 地心惯性坐标系 $I$;
- 追踪航天器本体坐标系 $B$;
- 目标航天器本体坐标系 $T$;
- 期望坐标系 $D$。
2. 轴角旋转
欧拉(Euler)转动定理:刚体绕定点的有限转动可以合成为绕经过该定点的某一直线的一次转动。因此,刚体的简单转动可以由旋转轴和旋转角唯一确定。
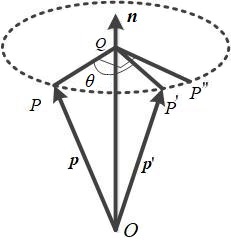
旋转矩阵 $\boldsymbol{R}$ 可以由旋转轴和旋转角唯一确定。假设位置矢量 $\boldsymbol{p}$ 绕定点旋转到位置矢量 $\boldsymbol{p}^\prime$,旋转轴为 $\boldsymbol{n}$,旋转角为 $\theta$,如下图所示。可以证明,$\boldsymbol{R}$ 可由 $\boldsymbol{n},\theta$ 显示表示。
从图中可以看出
\[\boldsymbol{p}^\prime = \vec{OQ} + \vec{QP^\prime}\]其中 $\vec{OQ}$ 是 $\boldsymbol{p}$ 平行于轴 $\boldsymbol{n}$ 的轴向分量,由正交分解有
\[\begin{aligned} \vec{OQ} &= \boldsymbol{n}\boldsymbol{n}^\top\boldsymbol{p}\\ \vec{QP^\prime} &= (\cos\theta)\vec{QP} + (\sin\theta)\vec{QP^{\prime\prime}} \end{aligned}\]又因为 $\vec{QP}$ 是 $\boldsymbol{p}$ 与垂直于轴 $\boldsymbol{n}$ 的垂向分量,由正交分解有
\[\vec{QP} = (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}^\top)\boldsymbol{p}\]根据矢量叉乘运算的几何意义,有
\[\vec{QP^{\prime\prime}} = \boldsymbol{n}\times\boldsymbol{p} = \boldsymbol{n}^\times\boldsymbol{p}\]带入可得
\[\vec{QP^\prime} = \cos{\theta}(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}^\top)\boldsymbol{p}+\sin{\theta}\boldsymbol{n}^\times\boldsymbol{p}\]综上
\[\boldsymbol{p}^\prime = \boldsymbol{n}\boldsymbol{n}^\top\boldsymbol{p}+\cos{\theta}(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}^\top)\boldsymbol{p}+\sin{\theta}\boldsymbol{n}^\times\boldsymbol{p} = \boldsymbol{R}\boldsymbol{p}\]则旋转矩阵为
\[\boldsymbol{R} = \boldsymbol{n}\boldsymbol{n}^\top+\cos{\theta}(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}^\top)+\sin{\theta}\boldsymbol{n}^\times\]3. 姿态四元数
3.1. 四元数定义
四元数由Hamilton在1843年提出,它可以看做是复数向 $\mathbb{R}^4$ 的推广。一个四元数定义为 \(\mathbb{H}=\{q:q=q_0+q_1i+q_2j+q_3k,\; q_0,q_1,q_2,q_3\in\mathbb{R}\}\)
四元数还可以表示为 $q=(q_0,\bar{q})$,其中 $q_0\in\mathbb{R}$ 是标量部分,$\bar{q} = [q_1, q_2, q_3]^\top\in\mathbb{R}^3$ 是矢量部分。
四元数的基本运算定义如下:
共轭:$q^* = (q_0,-\bar{q})\in\mathbb{H}$
范数(的平方):$\Vert q\Vert^2 = qq^* = q^*q=q\cdot q=(q_0^2+\bar{q}\cdot \bar{q},\bar{0})$
当四元数的范数限制为 1 时,就叫单位四元数,即
\[\mathbb{H}^u=\{q\in \mathbb{H}: q\cdot q=(1,0,0,0)\}\]3.2. 四元数表示旋转
三维空间中的旋转可以被认为是一个函数 $\phi$ ,从 $\mathbb{R}^3$ 到自身的映射。函数 $\phi$ 要想表示一个旋转,必须在旋转过程中保持向量长度(lengths)、向量夹角(angles)和 handedness 不变。handedness 和左右手坐标系有关,例如左手坐标系中向量旋转后,仍要符合左手坐标系规则。
3.3. 姿态四元数
单位四元数可以用来表示两个坐标系之间的相对姿态,此时又可称其为旋转四元数。若本体坐标系 $B$ 相对于惯性系 $I$ 的姿态用欧拉旋转轴角表示为 $(\bar{n},\theta)$,即本体坐标系 $B$ 绕着单位轴 $\bar{n}$ 旋转角度 $\theta$ 到达惯性坐标系 $I$。那么本体坐标系 $B$ 相对于惯性坐标系 $I$ 的姿态四元数为
\[q_{B/I}=(cos(\frac{\theta}{2}),\ sin(\frac{\theta}{2})\bar{n})\]如果旋转角度被限制在 $-180^{\circ}< \theta < 180^{\circ}$,那么四元数标量部分可以由下式计算
\[q_0 = \sqrt{(1-\vert\vert \bar{q} \vert\vert ^2)}\]注意,相对姿态轴角表示中, $(-\bar{n},-\theta)$ 和 $(\bar{n},\theta)$ 起到的旋转效果相同。带入姿态四元数定义式,可以得到惯性系相对于本体系的姿态四元数
\[q_{I/B} = q_{B/I}^*\]即姿态四元数(单位四元数)本身与其共轭四元数互为逆变换。
4. 向量的坐标变换
【定理1】假设坐标系 $Y$ 相对于坐标系 $X$ 的姿态四元数为 $q_{Y/X}$,矢量 $\bar{v}$ 再两个坐标系内的表示分别为 $\bar{v}^Y$ 和 $\bar{v}^X$,则有如下转换关系成立
\[v^Y = q^*_{Y/X}\cdot v^X \cdot q_{Y/X},\quad v^X = q^*_{X/Y}\cdot v^Y \cdot q_{X/Y}\]其中 $v^Y = [0,\bar{v}^Y],\ v^X = [0,\bar{v}^X]$。上式等价为
\[v^Y = R_X^Y\cdot v^X,\quad v^X = R_Y^X\cdot v^Y\]其中,坐标系 $Y$ 到坐标系 $X$ 的坐标旋转矩阵为
\[R_Y^X = \bar{n}\bar{n}^\top+\cos\theta(I_3-\bar{n}\bar{n}^\top)+\sin\theta \bar{n}^{\times}\]5. 姿态变换与四元数乘法
假设坐标系 $A$ 相对于坐标系 $B$ 的四元数为 $q_{A/B}$,坐标系 $B$ 相对于坐标系 $C$ 的四元数为 $q_{B/C}$,那么坐标系 $A$ 相对于坐标系 $C$ 的四元数为
\[q_{A/C} = q_{A/B} \otimes q_{B/C}\]6. 参考文献
[1] 皮皮夏. 【知乎】刚体的转动和旋转变换
[2] 皮皮夏. 【知乎】四元数代数以及姿态动力学建模
[3] lxycg. 【知乎】四元数和旋转(Quaternion & rotation)