强化学习（马尔可夫决策过程）

本文介绍了强化学习的基本概念和模型，主要包括马尔可夫过程、马尔可夫奖励过程和马尔可夫决策过程。

1. 强化学习
2. 马尔可夫过程（MP）
- 2.1. 基本概念
- 2.2. 环境
3. 马尔可夫奖励过程（MRP）
4. 马尔可夫决策过程（MDP）
5. 参考文献

1. 强化学习

强化学习是机器学习领域之一，受到行为心理学的启发，主要关注智能体如何在环境中采取不同的行动，以最大限度地提高累积奖励。强化学习是除了监督学习和非监督学习之外的第三种基本的机器学习方法。与监督学习不同的是，强化学习不需要带标签的输入输出对，同时也无需对非最优解的精确地纠正。

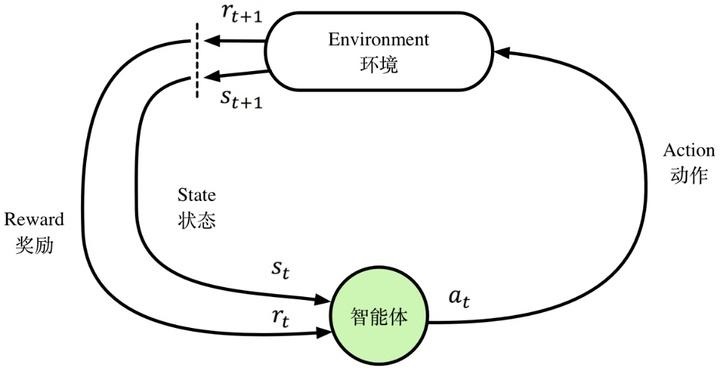
强化学习主要由智能体（Agent）、环境（Environment）、状态（State）、动作（Action）、奖励（Reward）组成。智能体执行了某个动作后，环境将会转换到一个新的状态，对于该新的状态环境会给出奖励信号（正奖励或者负奖励）。随后，智能体根据新的状态和环境反馈的奖励，按照一定的策略执行新的动作。上述过程为智能体和环境通过状态、动作、奖励进行交互的方式。

在每个时刻 $t$，智能体观察到所在的环境状态记为 $s_t$，，并再次基础上选择一个动作 $a_t$。作为动作的结果，智能体接收到一个数值化的奖励 $r_{t+1}$，并转移到一个新的状态 $s_{t+1}$ 。

如此反复迭代交互，可以得到一个序列或轨迹（trajectory）。

强化学习的朴素目标：训练智能体尽可能多的收集奖励。

1.1. 状态空间

1.1.1. 状态

「状态」$s$ 是对环境当前所处环境的完整描述，对于状态来说环境的所有信息都是可知的。在数学上，状态空间是一系列状态组成的集合 $\mathcal{S}$，其中 $s \in \mathcal{S}$。

在深度强化学习中，我们通常会使用实值向量vector、矩阵 matrix 或者高维张量 tensor 来表示状态。比如，视觉的状态可以表示为像素值构成的 RGB 矩阵，机器人的状态则可以表示为其关节角度和速度。

1.1.2. 观测

「观测」$o$ 则是一个状态的部分描述，可能会忽略一些信息，其同样可用实值向量vector、矩阵 matrix 或者高维张量 tensor 来表示。

当智能体能够观测到环境的全部状态时，这样的环境是可完全观测的 fully observed；当智能体只能观测到部分状态时，这样的环境称为可部分观测 partially observed。

「注」：在强化学习的公式中我们经常会看到表示状态的符号 $s$，但是实际上更准确的用法应该是使用表示观测的符号 $o$。比如，当我们探讨智能体如果进行动作决策时，公式中通常会说动作是基于状态的，但是「实际上动作是基于观测的」，因为智能体是无法直接感知到状态的。为了遵循惯例，之后的公式仍然会使用符号 $s$。

1.2. 动作空间

「给定的环境中有效的动作集合称为动作空间」。动作是对状态而言的，不同的状态可能有不同的动作空间，因此动作空间是一个与状态有关的集合。动作可以表示为 $\mathcal{A}(s),\; \forall s\in \mathcal{S}$。

「动作空间是离散的还是连续的」在强化学习问题中非常重要，有些方法只适合用于其中一个场景，所以这点需要特别关注。有些环境中（比如 Atari 和 Go），「动作空间是离散的」discrete，也就是说智能体的动作数量是有限的；而有些环境中（比如机器人控制），「动作空间是连续的」continuous，这些空间中动作通常用实值向量表示。

1.3. 策略

强化学习是从环境状态到动作的映射学习，称该映射关系为策略。通俗的理解，即智能体如何选择动作的思考过程称为策略。

最简单的策略可以是固定策略，如不管什么情况都执行特定动作。也可以采用规则策略，即满足什么条件下执行什么动作。也可以采用随机策略，即按照某个概率采样来选取动作。

2. 马尔可夫过程（MP）

2.1. 基本概念

几个基本概念定义如下：

马尔可夫性（Markov property）：在一个时序过程中，如果 $t＋1$ 时刻的状态仅取决于 $t$ 时刻的状态 $s_t$ 而与 $t$ 时刻之前的任何状态都无关时，则认为 $t$ 时刻的状态 $s_t$ 具有马尔可夫性，数学表述为 $p(s_{t+1}\vert s_{t},\cdots, s_1 ) = p( s_{t+1} \vert s_t)$
马尔科夫过程（Markov Process）：若过程中的每一个状态都具有马尔科夫性，则这个过程具备马尔科夫性。具备了马尔科夫性的随机过程称为马尔科夫过程，
马尔可夫链（Markov chain）：离散状态空间的马尔可夫过程称为马尔科夫链（Markov chain）。

马尔可夫过程中的三个概念：

采样（sample）或抽样：从符合马尔科夫过程给定的状态转移概率矩阵生成一个轨迹或回合的过程
轨迹（trajectory）或序列：采样得到的一条无限长的状态序列,如：$s_1-s_2-s_3-…$
回合（episode）或情节：采样直至一个终止状态，形成一条完整的状态序列。如：$s_1-s_2-s_3-\cdots-s_T$

2.2. 环境

环境是智能体交互的对象，是智能体在某状态下采取某动作后转移到新状态的最终参与者。以自动驾驶为例，在某个雨天的行驶状态下，智驾决定在 $120$ km/h 车速下（状态 $s_1$）向左打方向盘（动作）变向超车，期望状态是变到左侧相邻车道，但由于雨天湿滑（环境）导致车子最终滑到路边（新状态 $s_2$）。但是如果换一个干燥的晴天，大概率车子会正常变到左侧相邻车道（新状态 $s_3$）。

上述例子比较直观体现了环境在状态转移中的作用，即在状态 $s_1$ 下动作 $a_1$ 的结果并不一定是某个确定的新状态，而是与实际环境有关。一般情况下，环境可以建模为一个状态转移概率矩阵 $P$。

在马尔可夫过程中，我们暂时还不用考虑动作的作用，因此可以假设雨天环境大概率滑到路边（$s_2$），状态转移矩阵的元素为：

\[\begin{aligned} P(s_2\vert s_1) &= 0.85\\ P(s_3\vert s_1) &= 0.15 \end{aligned}\]

用二元组 $<S,P>$ 表述马尔可夫过程。其中，$S$ 为状态，$P$ 为不同状态间的转移概率，如状态 $s$ 到 $s^\prime$ 的状态转移概率

\[P_{s s^\prime}=P_{s s^\prime}=\mathbb{P}[S_{t+1}=s^\prime \vert S_t = s]\]

从上式也可以看到，下一时刻的状态$S_{t+1}$ 仅与当前时刻的状态 $S_t$ 有关，而与 $S_1,\cdots,S_{t-1}$ 无关。注意：这里的记号非常严谨， $S_{t}, S_{t+1}$ 代表某一时刻的状态，而 $s,s^\prime$ 代表某一种具体的状态类型。而在实际情况下，人们会将其简写多种不同的形式，需要特别注意

\[P_{s s^\prime}=P=p(S_{t+1}=s^\prime \vert S_{t}=s)=p(s^\prime \vert s) = p(s_{t+1} \vert s_{t})\]

对于离散的状态空间，为了描述整个状态空间中不同类型状态之间的关系，自然用矩阵表示，即：

\[P= \begin{bmatrix} p(s_1\vert s_1) & p(s_2\vert s_1) &\dots & p(s_n\vert s_1)\\ p(s_1\vert s_2) & p(s_2\vert s_2) &\dots & p(s_n\vert s_2)\\ \vdots & \vdots & \ddots &\vdots\\ p(s_1\vert s_n) & p(s_2\vert s_n)&\dots & p(s_n\vert s_n)\\ \end{bmatrix}\]

显然状态转移概率矩阵 $P$ 的规模是所有状态类型数 $n$ 的平方。且从一个状态转移到所有可能状态的概率之和为 $1$。

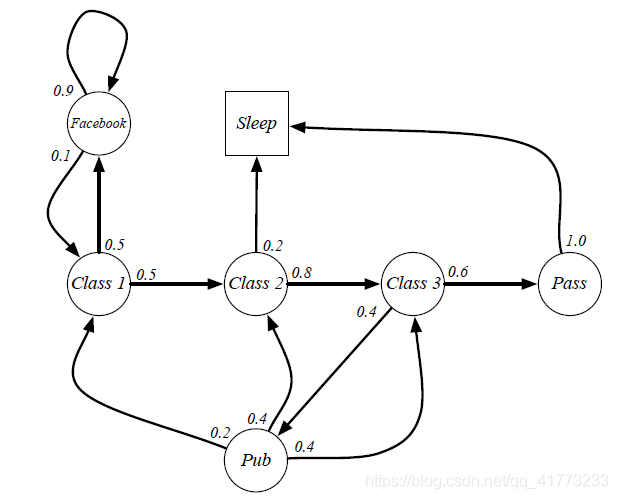
以下图为例：

不难写出状态转移概率矩阵：

\[\begin{aligned} &\quad C1\;\;\;C2\;\;\;C3\;\;\;Pass\;Pub\;FB\;\;Sleep\\ P= \begin{array}{r} C1\\ C2\\ C3\\ Pass\\ Pub \\ FB\\ Sleep \end{array} &\begin{bmatrix} 0& 0.5 &0&0&0&0.5&0\\ 0&0&0.8&0&0&0&0.2\\ 0&0&0&0.6&0.4&0&0\\ 0&0&0&0&0&0&1\\ 0.2&0.4&0.4&0&0&0&0\\ 0.1&0&0&0&0&0.9&0\\ 0&0&0&0&0&0&1\\ \end{bmatrix} \end{aligned}\]

3. 马尔可夫奖励过程（MRP）

马尔可夫奖励过程（Markov Reward Process，MRP）就是在马尔可夫过程中增加了奖励（收益） $R$ 项和奖励因子 $\gamma$。

表述一个马尔可夫奖励过程需要四元组 $<S,P,R,\gamma>$，其中：

$S$ 是一个有限状态集；
$P$ 是集合中状态转移概率矩阵：$P_{s s^\prime}=\mathbb{P}[S_{t+1}=s^\prime \vert S_t = s]$
$R$ 是奖励（收益）函数：$R_t = \mathbb{E}[R_{t+1}\vert S_t=s]$
$\gamma$ 是折扣因子：$\gamma \in [0,1)$

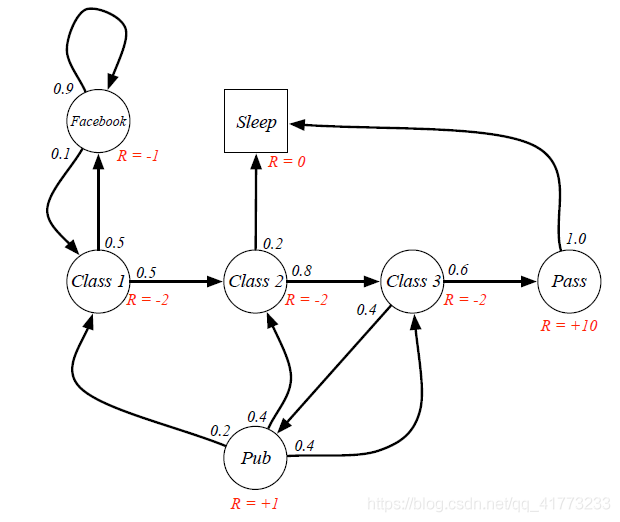
如下图所示

3.1. 奖励（Reward）

3.1.1. 奖励的定义

某时刻 $t$ 的即时奖励（immediate reward） $R_t$ 定义为从该时刻所处状态转移到下一时刻状态后从环境获得的标量数值。它是环境直接返回的反馈值，这个值可以是确定的，也可以是随机的（从某个概率分布中采样得到），具体取决于环境的定义。如果环境是随机的，即时奖励可能是一个随机变量，但从单次交互的角度来看，它是一个具体的标量值。

\[r_{t+1} = r(s_t)\]

关于下标为何为 $t+1$ 而不是 $t$，是因为通常约定奖励是离开当前状态后在下一时刻才获得的。

在后续马尔可夫决策过程中，其是与下一时刻状态 $s_{t+1}$ 一同被环境所返回的。

3.1.2. 与动作的关系

即时奖励与动作有关，因此在后续马尔可夫决策过程中，奖励可以表述为

\[r_{t+1} = r(s_t,a_t)\]

3.1.3. 与下一时刻状态的关系

奖励是环境赋予的，其与下一时刻是否有关取决于环境的定义。从正常的思维来讲，奖励当然与下一时刻的状态有关系的（比如状态转移后进入终点导致获得正奖励，或者进入陷阱导致获得负奖励）。这种情况下，奖励应表述为

\[r_{t+1} = r(s_t,a_t,s_{t+1})\]

但我们通常约定，奖励函数只依赖于当前状态和动作，与下一时刻无关。

在后续马尔可夫决策过程中，强调下一时刻的奖励和下一时刻的状态是被环境一起决定的。这导致离开当前状态获得的奖励是概率性的，我们需要求解它的期望
\[r_{t+1} = \mathbb{E}[r\vert s_t,a_t] = r\cdot p(r\vert s_t,a_t) = r\cdot \sum_{s_{t+1}}p(r\vert s_t,a_t,s_{t+1})p(s_{t+1}\vert s_t,a_t)\]
可以发现，即使奖励和下一时刻状态有关，这种相关性也可以通过状态转移概率来体现。

此时，强化学习的目标：使得智能体收到的累计奖励最大化。

对于无限长度的采样轨迹，奖励的期望是无限大的，所以需要做出一个折扣，以便在远期奖励的期望值有较好的收敛性。这就引入了回报和折扣因子的必要性。

3.2. 回报（Return）

某时刻 $t$ 的回报（收益）定义为从时刻 $t$ 开始的采样一条状态序列得到的所有奖励的折扣和：

\[G_t\doteq r_{t+1}+\gamma r_{t+2}+...=\sum_{k=0}^\infty \gamma^k r_{t+k+1}\]

其中 $\gamma \in [0,1)$ 被称为折扣因子，通常取值为 $0.9$。设置折扣因子的原因如下：

数学表达的方便，这也是最重要的
保证奖励的收敛性，避免陷入无限循环
远期利益具有一定的不确定性
符合人类更看重眼前利益的性格

折扣因子可以作为强化学习的一个超参数来进行调整，折扣因子不同就会得到不同行为的智能体：

折扣因子接近 $0$ 则表明趋向于“近视”性评估；
折扣因子接近 $1$ 则表明偏重考虑远期的利益。

前述例子中，假设从 $Class 1$ 状态开始到 $Sleep$ 状态终止，折扣因子 $\gamma = 0.5$，采样两条序列计算回报如下：

episode 1: C1 - C2 - C3 - Pass - Sleep
G_1 = -2 + 1/2 × (-2) + 1/4 × (-2) + 1/8 × (+10) = -2.25
episode 2: C1 - FB - FB - C1 - C2 - Sleep
G_2 = -2 + 1/2 × (-1) + 1/4 × (-1) + 1/8 × (-2) + 1/16 ×(-2) = -3.125

此时，强化学习的目标：使得智能体收到的回报最大化。

回报值是针对一次完整的采样序列的结果，存在很大的样本偏差。即 $G(s)$ 是从 $t$ 时刻的状态到终止状态的一条状态转移序列的回报值，但从 $t$ 时刻的状态到终止状态的马尔可夫链不止一条，每一条都有对应的采样概率和回报。对于复杂问题而言，要想精确的计算出 $G(s)$ 是几乎不可能的，因为无法穷举所有序列。

为了能够评估状态的好坏，引入新概念：价值函数。

3.3. 价值函数

价值函数（Value Function）：从某个状态 $s_t$ 开始的回报的期望，也即从某个状态 $s_t$ 开始采样无数条完整状态序列的回报的平均值，即

\[V(s_t) = \mathbb{E}[G_t \vert S_t=s_t]\]

对于马尔可夫奖励过程，价值函数即为状态价值函数。

以前面的例子，如果仅观测到两个序列，那么在状态 Class 1 处的学生的值函数就是 2 个回报值除以 2 即可。

v(Class1) = (G_1 + G_2) / 2 = ( (-2.25) + (-3.125)) / 2 = -2.6875

状态值函数的引入，从数学上解决了回报 $G(s)$ 计算时依赖大量采样，难以实际应用的问题。

但状态价值函数也不好算，因为在计算某个状态时候需要使用到将来所有状态的 $G(s)$。为了便于计算，对价值函数进行展开

\[\begin{aligned} V(s_t) &= \mathbb{E}[G_t \vert S_t=s_t]\\ &=\mathbb{E}[r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+...\vert S_t=s_t]\\ &=\mathbb{E}[r_{t+1}+\gamma (r_{t+2}+\gamma r_{t+3}+...)\vert S_t=s_t]\\ &=\mathbb{E}[r_{t+1}+\gamma G_{t+1}\vert S_t=s_t]\\ &=\mathbb{E}[r_{t+1}\vert S_t=s]+\gamma \mathbb{E}[G_{t+1}\vert S_t=s_t]\\ &=R_{s}+\gamma \mathbb{E}[G_{t+1}\vert S_t=s_t] \end{aligned}\]

上式中，第一项 $R_s$ 对应即时奖励的期望

\[R_s = \sum_{a}\pi(a\vert s)\sum_r(p(r\vert s,a)\cdot r)\]

第二项则代表了长期的潜在奖励。可以看出，长期潜在奖励的计算需要获取下一时刻状态对应回报的期望。然而，未来时刻的状态及其回报是不确定的，即

\[\mathbb{E}[G_{t+1}\vert S_t=s_t]\]

依然是一个很难求解的期望形式。因此直接计算价值函数是不现实的。下面介绍贝尔曼方程来计算价值函数。

3.4. 贝尔曼方程

[ 推导 1 ]：

定义：如果 $X$ 和 $Y$ 都是离散型随机变量，则条件期望（Conditional Expectation）定义为 $\mathbb{E}[Y\vert X=x]=\sum_y yP(Y=y\vert X=x)$

定义：如果 $X$ 是随机变量，其期望为 $\mathbb{E}[X]$，$Y$ 为相同概率空间上的任意随机变量，则有全期望（Total Expectation）公式 $\mathbb{E}[X] = \mathbb{E}[\mathbb{E}[X\vert Y]]$

现证明（主要证明第一个等式）

\[\mathbb{E}[G_{t+1}\vert S_t=s_t] = \mathbb{E}[\mathbb{E}[G_{t+1}\vert S_{t+1}]\vert S_t=s_t] = \mathbb{E}[V(s_{t+1})\vert S_t=s_t]\]

为了推导简便，另 $s_{t+1} = s^\prime$，$s_t=s$，有

\[\begin{aligned} \mathbb{E}[\mathbb{E}[G_{t+1}\vert S_{t+1}]\vert S_t=s] &= \mathbb{E}\left[\sum_{g^\prime}g^{\prime}P(G(s^\prime)=g^{\prime}\vert S_{t+1})\vert s\right]\quad (条件期望)\\ &=\sum_{s^\prime} \sum_{g^\prime}g^{\prime}P(G(s^\prime)=g^{\prime}\vert S_{t+1}=s^\prime, s)P(S_{t+1}=s^\prime\vert s)\\ &=\sum_{s^\prime} \sum_{g^\prime}g^{\prime} \frac{P(G(s^\prime)=g^{\prime}\vert S_{t+1}=s^\prime, s)P(S_{t+1}=s^\prime\vert s)\cdot P(s)}{P(s)} \\ &=\sum_{s^\prime} \sum_{g^\prime}g^{\prime} \frac{P(G(s^\prime)=g^{\prime}\vert S_{t+1}=s^\prime, s)P(S_{t+1}=s^\prime, s)}{P(s)} \\ &=\sum_{s^\prime} \sum_{g^\prime}g^{\prime} \frac{P(G(s^\prime)=g^{\prime}, S_{t+1}=s^\prime, s)}{P(s)} \\ &=\sum_{s^\prime} \sum_{g^\prime}g^{\prime} P(G(s^\prime)=g^{\prime}, S_{t+1}=s^\prime \vert s) \\ &=\sum_{g^\prime} \sum_{s^\prime}g^{\prime} P(G(s^\prime)=g^{\prime}, S_{t+1}=s^\prime \vert s) \\ &=\sum_{g^\prime}g^{\prime} P(G(s^\prime)=g^{\prime} \vert s) \\ &=\mathbb{E}[G(s^\prime)\vert s]=\mathbb{E}[G_{t+1}\vert s_t] \end{aligned}\]

得证。则当前时刻的状态价值函数

\[\begin{aligned} V(s_t)&=R_{s}+\gamma \mathbb{E}[G_{t+1}\vert S_t=s_t]\\ &=R_{s}+\gamma \mathbb{E}[V(s_{t+1})\vert S_t=s_t]\\ &=R_{s}+\gamma \sum_{s_{t+1}\in S} V(s_{t+1})P(s_{t+1}\vert s_t) \end{aligned}\]

上式即为马尔可夫奖励过程的贝尔曼方程。

[ 推导 2 ]：

对后项进行全概率展开

\[\begin{aligned} \gamma \mathbb{E}[G_{t+1}\vert S_t=s_t] &= \gamma \sum_{s_{t+1}\in S}\mathbb{E}[G_{t+1}\vert S_{t+1}=s_{t+1}]P(s_{t+1}\vert s_t)\\ &= \gamma \sum_{s_{t+1}\in S} V(s_{t+1})P(s_{t+1}\vert s_t) \end{aligned}\]

上面第二步是因为（根据价值的定义）

\[V(s_{t+1}) = \mathbb{E}[G_{t+1} \vert S_{t+1} = s_{t+1}]\]

最终得到

\[V(s_t) = r_{s}+\gamma \sum_{s_{t+1}\in S} V(s_{t+1})P(s_{t+1}\vert s_t)\]

即为马尔可夫奖励过程的贝尔曼方程。

贝尔曼方程刻画了当前状态 $s_t$ 和下一个状态 $s_{t+1}$ 之间的关系。可以看出，当前状态的价值函数可以通过下一个状态的价值函数来迭代计算。

若将马尔可夫奖励过程的状态构成 $n$ 维状态空间，贝尔曼方程可以写成矩阵形式

\[\begin{aligned} \begin{bmatrix} V(s_1)\\ V(s_2)\\ \vdots\\ V(s_n) \end{bmatrix} &= \begin{bmatrix} R(s_1)\\ R(s_2)\\ \vdots\\ R(s_n) \end{bmatrix} +\gamma \begin{bmatrix} P(s_1\vert s_1) & P(s_2\vert s_1)& \cdots & P(s_n\vert s_1)\\ P(s_1\vert s_2) & P(s_2\vert s_2)& \cdots & P(s_n\vert s_2)\\ \vdots & \vdots & \ddots & \vdots\\ P(s_1\vert s_n) & P(s_2\vert s_n)& \cdots & P(s_n\vert s_n)\\ \end{bmatrix} \begin{bmatrix} V(s_1)\\ V(s_2)\\ \vdots\\ V(s_n) \end{bmatrix}\\ \boldsymbol{V} &= \boldsymbol{R}+\gamma \boldsymbol{P} \boldsymbol{V}\\ \end{aligned}\]

上述是个线性方程组，可直接得到闭式解

\[\boldsymbol{V} = (\boldsymbol{I}-\gamma\boldsymbol{P})^{-1}\boldsymbol{R}\]

需要注意的是，矩阵求逆的复杂度为 $O(n^3)$，因此直接求解仅适用于状态空间规模小的问题。状态空间规模大的问题的求解通常使用迭代法，在后续介绍马尔可夫决策过程时进行详细介绍。

注意到，只有当 $P$ 已知的情况下，也就是模型已知时，才可以得到解析形式的闭式解。

4. 马尔可夫决策过程（MDP）

马尔可夫决策过程是在马尔可夫奖励过程的基础上加入了决策，即增加了动作。其定义为：

马尔科夫决策过程是一个五元组 $<S,A,P,R,\gamma>$，其中

$S$ 是有限数量的状态集
$A$ 是有限数量的动作集
$P$ 是状态转移概率，$P_{ss^\prime}^a=\mathbb{P}[S_{t+1} = s^\prime \vert S_t = s, A_t=a]$
$R$ 是一个奖励函数，$R_{s}^a=\mathbb{E}[R_{t+1} \vert S_t = s, A_t=a]$
$\gamma$ 是一个折扣因子，$\gamma \in [0,1)$

从上面定义可以看出，马尔可夫决策过程的状态转移概率和奖励函数不仅取决于智能体当前状体，还取决于智能体选取的动作。而马尔可夫奖励过程仅取决于当前状态。

4.1. 动作（Action）

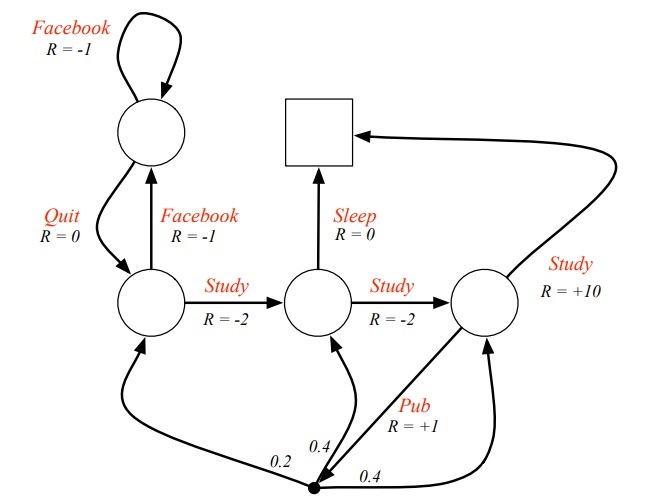
以下图为例：

图中红色的文字表示学生采取的动作，而不是 MRP 时的状态名。对比之前的学生 MRP 示例可以发现，即时奖励与动作有关了，同一个状态下采取不同的动作得到的即时奖励是不一样的。

由于引入了动作，容易与状态名称混淆，因此此图没有给出各状态的名称；此图还把 Pass 和 Sleep 状态合并成一个终止状态；另外当选择”去查阅文献（Pub）”这个动作时，主动进入了一个临时状态（图中用黑色小实点表示），随后被动的被环境按照其动力学分配到另外三个状态，也就是说此时智能体没有选择权决定去哪一个状态。

可以看出，状态转移概率 $P_{ss^\prime}^a$ 和奖励函数 $R_{s}^a$ 均与当前状态 $s$ 下采取的动作 $a$ 有关。由于动作的选取不是固定的，因此引入新概念：策略。

4.2. 策略（Policy）

策略 $\pi(a\vert s)$ 是从状态 $s$ 到每个动作 $a$ 的选择概率之间的映射，即

\[\pi(a\vert s) = \mathbb{P}[A_t=a \vert S_t=s]\]

一个策略完整地定义了智能体的行为方式，即策略定义了智能体在各种状态下可能采取的动作，以及在各种状态下采取各种动作的概率。MDP的策略仅与当前的状态有关，与历史信息无关；同时某一确定的策略是静态的，与时间无关；但是个体可以随着时间更新策略。

给定一个马尔可夫决策过程 $<S,A,P,R,\gamma>$ 和一个策略 $\pi$ 后，相应的状态转移概率 $P_{ss^\prime}^\pi$ 和奖励函数 $R_{s}^\pi$ 可更新描述如下

\[\begin{aligned} P_{ss^\prime}^\pi &= \sum_{a\in A}\pi(a\vert s)P_{ss^\prime}^a\\ R_{s}^\pi &= \sum_{a\in A}\pi(a\vert s)R_{s}^a \end{aligned}\]

对应的 $<S,P^\pi,R^\pi,\gamma>$ 是一个马尔可夫奖励过程， $<S,P^\pi>$ 是一个马尔可夫过程。

4.3. 动态特性

在有限 MDP 中，状态、动作和奖励的集合（$S, A, R$）都只有有限个元素。在这种情况下，随机变量 $R_t$ 和 $S_t$ 具有定义明确的离散概率分布，并且之依赖于前一时刻的状态和动作。也就是说，给定前一时刻的状态和动作的值时，这些随机变量的特定值 $s^\prime \in S, r^\prime \in R$ 在 $t$ 时刻出现的概率为

\[p(s^\prime,r \vert s,a) \doteq \mathbb{P}\{S_t=s^\prime, R_t=r \vert S_{t-1}=s, A_{t-1}=a\}\]

函数 $p$ 定义了 MDP 的动态特性。动态特性函数是一个描述 $t-1$ 和 $t$ 前后两个相邻时刻的随机变量间动态关系的条件概率。

在 MDP 中，由 $p$ 给出的概率完全刻画了环境的动态特性，即$S_t,R_t$ 的每个可能的值出现的概率只取决于前一个状态 $S_{t-1}$ 和动作 $A_{t-1}$，且与更早时刻的状态和动作无关（马尔可夫性）。

4.3.1. 状态转移概率

从四参数动态函数 $p$ 中，可以计算出关于环境的任何其它信息。比如，想表达MDP的状态转移过程，可以将随机变量 $R$ 求积分得到 状态转移概率

\[P_{ss^\prime}^a = p(s^\prime \vert s,a) \doteq \mathbb{P}\{ S_t=s^\prime \vert S_{t-1}=s, A_{t-1}=a \} = \sum_{r\in R}p(s^\prime,r \vert s,a)\]

所以，整个马尔可夫决策过程的全部信息包含在状态变量集合 $A$，$S$，$R$ 和函数空间 $P$ 中，每个时刻都有一个 $A_t$，$S_t$，$R_t$，每两个相邻时刻之间都有一个 $p_t$。

4.3.2. 奖励概率

类似地，状态动作 $s,a$ 对的期望奖励可以写作两个参数的函数

\[r(s,a) = \mathbb{E}_\pi [R_{t+1} \vert S_t = s] = \sum_{r\in R} r \sum_{s^\prime \in S} p(s^\prime, r \vert s,a)\]

想表达 MDP 的即时奖励获取过程，可以将对 $s^\prime$ 求积分得到 奖励概率

\[P_{ss^\prime}^r = p(r \vert s,a) = \sum_{s^\prime \in S}p(s^\prime, r \vert s,a)\]

4.4. 价值函数

马尔可夫决策过程中，价值函数分为状态价值函数和动作价值函数。

4.4.1. 状态价值函数

状态价值函数（state-value Function）是从某个状态 $s$ 开始，执行策略 $\pi$ 所获得的回报的期望；也即在执行当前策略时，衡量智能体处在状态 $s$ 时的价值大小。即

\[v_\pi(s) \doteq \mathbb{E}_\pi[G_t \vert S_t=s]\]

注意，终止状态的价值始终为零。我们把函数 $v_{\pi}(s)$ 称为策略 $\pi$ 的状态价值函数。

状态价值函数衡量了一个状态的好坏，好的状态拥有较大的状态价值函数，表明从这个状态出发，预期能获得更高的回报。

4.4.2. 动作价值函数

类似地，我们把策略 $\pi$ 下在状态 $s$ 时采取动作 $a$ 的价值即为 $q_\pi(s,a)$。即根据策略 $\pi$，从状态 $s$ 开始，执行动作 $a$ 之后，所有可能的决策序列的期望回报

\[q_\pi(s,a) \doteq \mathbb{E}_\pi[G_t \vert S_t=s, A_t=a]\]

状态-动作价值函数衡量了某个状态下不同动作的好坏，好的状态-动作拥有较大的状态-动作价值函数，表明从这个状态出发选择这个动作，预期能获得更高的回报。

4.4.3. 二者的意义

如何理解强化学习中的Q值和V值？ https://zhuanlan.zhihu.com/p/109498587

强化学习-1-Q_Table based Method https://zhuanlan.zhihu.com/p/138291295

状态价值函数是对状态的价值的衡量。从某个状态出发，依据特定策略 $\pi$ 采用不同动作，在环境的影响下进行状态转移。

动作价值函数是对某状态下特定动作的价值的衡量。从某个状态出发，采取特定的动作 $a$，在环境的影响下进行状态转移；后续依据特定策略 $\pi$ 采用不同动作，在环境的影响下进行状态转移。

强化学习模型的好坏，主要取决于在当前状态下，是否能选择出收益最大的动作，因此 $q(s,a)$ 的精准预估显得十分重要。

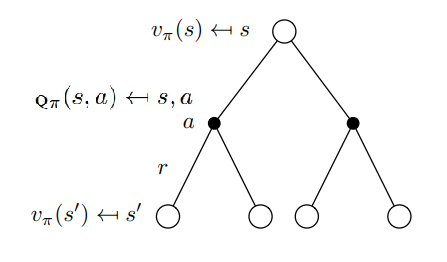
4.4.4. 回溯图与回溯操作

回溯操作就是将后继状态（或“状态-动作”二元组）的价值信息回传给当前时刻的状态（或”状态-动作“二元组），可以用回溯图来表示，这是强化学习的核心内容。

典型的回溯图如下

严谨地说，$q_\pi$ 和 $v_\pi$ 的作用是评估给定策略 $\pi$ 的价值，也就是一直使用这个策略来选取动作能得到的期望回报。不同之处是，$v_\pi$ 评估的对象是状态，考虑从状态 $s$ 出发，遵循策略 $\pi$ 得到的期望回报；$q_\pi$ 评估的对象是一个状态-动作对，考虑从状态 $s$ 出发，执行动作 $a$ 之后，遵循策略 $\pi$ 得到的期望回报。

因此，$v_\pi$ 可以写成 $q_\pi$ 关于策略 $\pi$（执行不同动作）的期望，$q_\pi$ 可以写成 $v_\pi$ 关于状态转移 $P_{ss^\prime}^a=p(s^\prime \vert s,a)$（执行动作 $a$ 后转移到不同状态）的期望。然后它们相互套娃，就得到了下面的两条等式，这两个等式也可以通过回溯图来直观理解。

[ 等式1 ]：

\[v_\pi(s) = \mathbb{E}_aq_\pi(s,a) = \sum_{a\in A}\pi(a\vert s)q_\pi(s,a)\]

上面回溯图的上半部分对应上述等式，描述了处于特定状态 $s$ 的价值。即在状态 $s$ 时，遵循策略 $\pi$ 后，状态 $s$ 的价值体表示为在该状态下采取所有可能动作的动作价值（$q$ 值）按该状态下动作发生概率（策略 $\pi$）的乘积求和。

从状态 $s$ 来看，我们有可能采取两种行动（图中黑点），每个动作都有一个 $q$ 值（状态-动作值函数）。对 $q$ 值进行平均，这个均值告诉我们在特定状态下有多好，也即 $v_\pi(s)$。

上述等式可以通过 $v_\pi(s)$ 的贝尔曼方程推导得到，即

\[\begin{aligned} v_\pi(s) &= \sum_{a, s^\prime, r}\pi(a\vert s)p(s^\prime,r \vert s,a)\cdot [ r+\gamma v_\pi(s^\prime) ]\\ &= \sum_{a}\pi(a\vert s)\cdot \sum_{s^\prime, r}p(s^\prime,r \vert s,a)\cdot [ r+\gamma v_\pi(s^\prime) ]\\ &=\sum_{a}\pi(a\vert s)\cdot \sum_{s^\prime, r}p(s^\prime,r \vert s,a)\cdot [r+\gamma r+\gamma^2 r+...\vert s,a]\\ &=\sum_{a}\pi(a\vert s)\cdot \mathbb{E}_\pi[G_t\vert s,a]\\ &=\sum_{a}\pi(a\vert s)\cdot q_\pi(s,a) \end{aligned}\]

[ 等式2 ]：

\[q_\pi(s,a) = \sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma v_\pi(s^\prime) \right]\]

证明如下

\[\begin{aligned} q_\pi(s,a) &= \mathbb{E}_\pi\left[ G_t \vert S_t=s, A_t=a \right]\\ &=\mathbb{E}_\pi\left[R_{t+1}+\gamma G_{t+1}\vert S_t=s, A_t=a \right]\\ &=\sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma \sum_{a^\prime} \pi(a^\prime \vert s^\prime) \mathbb{E}_\pi [G_{t+1} \vert S_{t+1}=s^\prime, A_{t+1}=a^\prime] \right]\\ &=\sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma \sum_{a^\prime} \pi(a^\prime \vert s^\prime) q_\pi(s^\prime, a^\prime) \right]\\ &=\sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma v_\pi(s^\prime) \right] \end{aligned}\]

上式也可以从回溯图中推导得出。

4.5. 贝尔曼方程

4.5.1. 状态价值函数的贝尔曼方程

与马尔可夫奖励过程中的价值函数类似，状态价值函数也有如下贝尔曼方程成立

\[\begin{aligned} v_\pi(s) &= \mathbb{E}_\pi[R_{t+1} + \gamma G_{t+1} \vert S_t = s]\\ &= \sum_a \pi(a\vert s) \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a) [ r+\gamma v_\pi(s^\prime) ],\; \forall s\in \mathcal{S} \end{aligned}\]

方程推导过程如下，首先易知第一项为即时奖励的期望

\[\begin{aligned} \mathbb{E}_\pi[R_{t+1}\vert S_t=s] &= \sum_a \pi(a\vert s)\mathbb{E} [R_{t+1}\vert S_t=s, A_t=a]\\ &= \sum_a \pi(a\vert s)\sum_{s^\prime} p(r \vert s,a) r\\ &=\sum_a\pi(a\vert s)\sum_{s^\prime}\sum_r p(s^\prime, r \vert s,a) r\\ \end{aligned}\]

第二项为未来奖励的折扣期望（推导中暂不关注折扣因子）

\[\begin{aligned} \mathbb{E}_\pi[G_{t+1}\vert S_{t}=s] &= \sum_{s^\prime}\mathbb{E}_\pi[G_{t+1}\vert S_{t}=s, S_{t+1}=s^\prime]p(s^\prime\vert s)\\ &= \sum_{s^\prime}\mathbb{E}_\pi[G_{t+1}\vert S_{t+1}=s^\prime]p(s^\prime\vert s)\quad (\text{Markov Property})\\ &=\sum_{s^\prime}v_\pi(s^\prime)p(s^\prime\vert s)\\ &= \sum_{s^\prime}v_\pi(s^\prime) \sum_a p(s^\prime \vert s,a) \pi(a\vert s)\\ &= \sum_{s^\prime} v_\pi(s^\prime)\sum_a\sum_r p(s^\prime,r \vert s,a) \pi(a\vert s) \\ &= \sum_a \pi(a\vert s) \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a) v_\pi(s^\prime) \end{aligned}\]

将上述两项推导加和，则有贝尔曼（期望）方程推导如下

\[\begin{aligned} v_\pi(s) &= \mathbb{E}_\pi[G_t \vert S_t=s]\\ &=\mathbb{E}_\pi[R_{t+1}+ \gamma G_{t+1}\vert S_t=s]\\ &=\sum_a \pi(a\vert s) \left[ \sum_{r} p(r \vert s,a) r+\gamma \sum_{s^\prime} p(s^\prime \vert s,a) v_\pi(s^\prime) \right]\\ &=\sum_a \pi(a\vert s) \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a) [ r+\gamma v_\pi(s^\prime) ] \\ &=\sum_{a, s^\prime, r}\pi(a\vert s)p(s^\prime,r \vert s,a)\cdot [ r+\gamma v_\pi(s^\prime) ] \end{aligned}\]

最后一行，通过将求和符号合并后，我们可以看出，上述状等式描述了一个关于三参数 $a\in A, s^\prime \in S, r\in R$ 在所有可能性上的求和。对于每一个三元组，我们计算出其概率 $\pi(a\vert s)p(s^\prime,r \vert s,a)$ 然后乘以方括号内的值作为权值，最后加权求和得到状态价值函数的期望。参考回溯图可以更好理解。

4.5.2. 矩阵化表述与迭代求解

与马尔可夫奖励过程类似，将状态价值函数的贝尔曼方程矩阵化，首先列写贝尔曼方程如下

\[v_\pi(s) =\sum_a \pi(a\vert s) \left[ \sum_{r} p(r \vert s,a) r+\gamma \sum_{s^\prime} p(s^\prime \vert s,a) v_\pi(s^\prime) \right]\]

令

\[\begin{aligned} r_\pi(s) &= \sum_a \pi(a\vert s)\sum_{r} p(r \vert s,a) r\\ p_\pi(s^\prime\vert s) &= \sum_a \pi(a\vert s)\sum_{r} p(s^\prime \vert s, a) \end{aligned}\]

则对于任意状态 $s_i \in \mathcal{S}\in \mathbb{R}^n$ 和其后续状态 $s_j \in \mathcal{S}\in \mathbb{R}^n$，有

\[v_\pi(s_i) = r_\pi(s) + \gamma \sum_{s_j}p_\pi(s_j\vert s_i)v_\pi(s_j)\]

将所有状态写成矩阵形式，有

\[\boldsymbol{V}_\pi = \boldsymbol{R}_\pi + \gamma \boldsymbol{P}_\pi \boldsymbol{V}_\pi\]

其中

\[\begin{aligned} \boldsymbol{V}_\pi &= [v_\pi(s_1),\cdots, v_\pi(s_n)]^\top \in \mathbb{R}^n\\ \boldsymbol{R}_\pi &= [r_\pi(s_1),\cdots, r_\pi(s_n)]^\top \in \mathbb{R}^n\\ \boldsymbol{P}_\pi &= [p_\pi(s_1\vert s_1),\cdots, p_\pi(s_1\vert s_n); \cdots; p_\pi(s_n\vert s_1),\cdots, p_\pi(s_n\vert s_n)] \in \mathbb{R}^{n\times n} \end{aligned}\]

则闭式解为

\[\boldsymbol{V}_\pi^* = (\boldsymbol{I}-\gamma \boldsymbol{P}_\pi)^{-1}\boldsymbol{R}_\pi\]

可通过迭代求解的方法规避矩阵求逆操作，即

\[\boldsymbol{V}_\pi^{(k+1)} = \boldsymbol{R}_\pi + \gamma \boldsymbol{P}_\pi \boldsymbol{V}_\pi^{(k)}\]

可证明，当 $k\rightarrow \infty$ 时，$V_\pi^{(k)}\rightarrow V_\pi^*$，证明如下：

定义误差

\[\delta^k = \boldsymbol{V}_\pi^{(k)} - \boldsymbol{V}_\pi^*\]

我们需要证明

\[\delta^k \rightarrow 0\]

有

\[\begin{aligned} \boldsymbol{V}_\pi^{(k)} &= \delta^k + \boldsymbol{V}_\pi^*\\ \boldsymbol{V}_\pi^{(k+1)} &= \delta^{k+1} + \boldsymbol{V}_\pi^*\\ \end{aligned}\]

代入迭代形式的贝尔曼方程，有

\[\begin{aligned} \delta^{k+1} + \boldsymbol{V}_\pi^* &= \boldsymbol{R}_\pi + \gamma \boldsymbol{P}_\pi (\delta^k + \boldsymbol{V}_\pi^*)\\ \delta^{k+1} &= -\boldsymbol{V}_\pi^* + \boldsymbol{R}_\pi + \gamma \boldsymbol{P}_\pi \delta^k + \gamma \boldsymbol{P}_\pi \boldsymbol{V}_\pi^*\\ \end{aligned}\]

注意到 $\boldsymbol{V}_\pi^*$ 同样也满足贝尔曼方程，因此

\[\begin{aligned} \delta^{k+1} &= -\boldsymbol{V}_\pi^* + (\boldsymbol{R}_\pi + \gamma \boldsymbol{P}_\pi \boldsymbol{V}_\pi^*) + \gamma \boldsymbol{P}_\pi \delta^k\\ &= \gamma \boldsymbol{P}_\pi \delta^k \end{aligned}\]

因此

\[\delta^{k+1} = \gamma \boldsymbol{P}_\pi \delta^k = \gamma^2 \boldsymbol{P}_\pi^2 \delta^{k-1} = \cdots = \gamma^{k+1} \boldsymbol{P}_\pi^{k+1} \delta^0\]

由于 $\gamma < 1,\; \gamma^{k+1}\rightarrow 0$，且 $0\leq \boldsymbol{P}_\pi^{k} < 1$（其每一行之和等于 $1$），所以当 $k\rightarrow \infty$ 时，$\delta^k \rightarrow 0$，证毕。

4.5.3. 状态-动作价值函数的贝尔曼方程

类似地，动作价值函数也有如下贝尔曼方程成立

\[\begin{aligned} q_\pi(s,a) &= \mathbb{E}_\pi[R_{t+1} + \gamma G_{t+1} \vert S_t = s, A_t = a]\\ &=\sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma \sum_{a^\prime} \pi(a^\prime \vert s^\prime) q_\pi(s^\prime, a^\prime) \right] \end{aligned}\]

4.6. 贝尔曼最优方程

4.6.1. 最优策略

强化学习的最终目标是寻找最优策略，最优策略是使得价值函数最大的策略

\[\pi^* \; \text{is optimal if}\; v_{\pi^*}(s)\geq v_\pi(s),\; \forall s\in\mathcal{S},\forall\pi\in\mathcal{\Pi}\]

这个定义引出了许多问题：

最优策略是否存在？因为定义里的最优策略非常理想，它比其他所有策略都要好，并且在所有状态上都能打败其它策略，那么是否存在这样的情况，最优策略在某些状态上能打败其它的策略，但是在某些状态上没法打败。

最优策略是否唯一？（分别使状态价值函数最大，和使状态-动作价值函数最大，这两个策略等价么？如果等价那么唯一么？）

最优策略是随机的还是确定的？

如何获得最优策略？

由于价值函数有两种，因此可分别定义如下两种最优策略：

\[\begin{aligned} \pi^* &= \mathop{\text{argmax}}\limits_\pi \;v_\pi(s)\\ \pi^o &= \mathop{\text{argmax}}\limits_\pi \;q_\pi(s,a)\\ \end{aligned}\]

其中最大状态价值函数可定义为

\[\begin{aligned} v_*(s) &\doteq \mathop{\text{max}}\limits_\pi \;v_\pi(s) = v_{\pi^*}(s)\geq v_\pi(s)\quad\forall s\in\mathcal{S},\forall\pi\in\mathcal{\Pi}\\ q_*(s,a) &\doteq \mathop{\text{max}}\limits_\pi \;q_\pi(s,a) = q_{\pi^o}(s,a)\geq q_\pi(s,a)\quad\forall s\in\mathcal{S},\forall\pi\in\mathcal{\Pi}\\ \end{aligned}\]

首先证明，对于不同的价值函数（即 $v_\pi(s)$ 和 $q_\pi(s,a)$），上述两种最优策略是等价的。

根据两个价值函数的关系有

\[v_\pi(s) = \sum_{a}\pi(a\vert s)\cdot q_\pi(s,a) = \mathbb{E}[q_\pi(s,a)]\]

对上式的策略统一取到令状态价值函数最大的最优策略，有

\[\begin{aligned} v_{\pi^*}(s) &= \max_a\sum_{a}\pi^*(a\vert s)\cdot q_\pi(s,a)\\ &=\max_a[\pi(a_1\vert s)q_\pi(s,a_1)+\cdots+\pi(a_n\vert s)q_\pi(s,a_n)]\\ \end{aligned}\]

等式右边可以看作对所有状态-动作价值函数的加权和求最大值，若其中某个状态-动作价值函数最大，其权重必然为 $1$，才能保证上式取到最大值。此时对应的策略可以写为

\[\pi^*(a\vert s) = \left\{ \begin{aligned} 1& \quad \text{if}\quad a=\text{argmax}_a q_{\pi^*}(s,a)\\ 0& \quad \text{otherwise} \end{aligned} \right.\]

我们发现，这个策略就是一个 $0-1$ 策略，对于不同的价值函数而言，最优策略是等价的

\[\pi^* = \mathop{\text{argmax}}\limits_\pi \;q_\pi(s,a) = \pi^o\]

4.6.2. 最优价值函数

已知状态价值函数是动作价值函数的期望（加权平均）

\[v_\pi(s) = \mathbb{E}_aq_\pi(s,a)\]

那么当取最优策略时，其必然取到最大值，即

\[v_*(s) = \mathop{\text{max}}\limits_a \; q_*(s,a)\]

将最优状态价值函数代入前述【等式2】，得到最优状态-动作价值函数的表达式

\[q_*(s,a) = \sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma v_*(s^\prime) \right]\]

4.6.3. 贝尔曼最优方程

将最优状态价值函数的代入改写贝尔曼方程，得到贝尔曼最优方程为

\[v_*(s) = \mathop{\text{max}}\limits_a \sum_{s^\prime}\sum_r p(s^\prime,r \vert s,a) [ r+\gamma v_*(s^\prime) ]\]

矩阵形式为

\[\boldsymbol{V} = \max_\pi(\boldsymbol{R}_\pi + \gamma\boldsymbol{P}_\pi\boldsymbol{V})\]

类似地，最优状态-动作价值函数对应的贝尔曼最优方程为

\[q_*(s,a) = \sum_{s^\prime,r}p(s^\prime,r \vert s,a) \left[r+\gamma \mathop{\text{max}}\limits_a \; q_*(s^\prime,a^\prime) \right]\]

贝尔曼最优方程给出了最优价值函数和最优策略的关系，即二者通过贝尔曼最优方程约束彼此，相互共同达到最优。但关于方程解的存在性和唯一性还有待进一步证明。

以状态价值函数的贝尔曼最优方程为例，定义贝尔曼算子：

\[\mathcal{B}(\boldsymbol{V}) = \max_\pi(\boldsymbol{R}_\pi + \gamma\boldsymbol{P}_\pi\boldsymbol{V})\]

其解（也即最优状态价值函数）是存在且唯一的，可通过不动点定理来证明。

不动点（fix point）：若 $x\in X$ 满足 $f(x)=x$，其中 $f:X\rightarrow X$，则 $x$ 为一个不动点

压缩映射（contraction mapping）：若 $f:X\rightarrow X$ 满足 $\Vert f(x)-f(y)\Vert\leq \lambda\Vert y-x\Vert$，其中 $\lambda<1$，则 $f$ 为一个压缩映射，其中 $d=\Vert \cdot \Vert$ 可以是任意向量范数

不动点定理：对于完备度量空间 $(X,d)$ 中任何形式的 $x=f(x)$ 方程，如果 $f$ 是压缩映射，那么满足：

存在性：存在一个不动点 $x^$ 使得 $f(x^)=x^*$

唯一性：不动点是唯一存在的

求解方法：考虑一个序列 $x_k$ 满足 $x_{k+1}=f(x_k)$，则 $x_k\rightarrow x^*, k\rightarrow \infty$，且收敛过程是呈指数级的

对于度量空间，我们使用 $L_\infty$ 范数

\[\Vert \boldsymbol{V}\Vert_{\infty} = \max_i \vert V_i \vert\]

根据此度量空间范数的定义，两个值函数之间的距离等于两个值函数向量各方向绝对值之差的最大值。同样，对于有限奖励的有限MDP，值函数将始终在实数空间中。因此，此有限空间是完备的。

定理：贝尔曼算子 $\mathcal{B}$ 是有限空间 $(X, L_\infty)$ 上的压缩映射。证明过程略，可参考《Mathematical Foundation of Reinforcement Learning》第 3.3.4 节。

上述定理保证了贝尔曼最优方程解的存在性和唯一性，并且保证可以通过迭代的形式求解得到最优价值函数（也即后文中的价值迭代（value iteration））。

4.6.4. 最优策略的求解

通过迭代求解得到最优价值函数后，如何确定最优策略？我们根据迭代求解的价值函数的类别分别讨论：

已知 $v_{*}$

为了求解最优策略，只需要做一步搜索就行。也就是对于不同的 $a\in A$，计算

\[\pi_*(a\vert s) \leftarrow \mathop{\text{argmax}}\limits_a \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma v_*(s^\prime)]\]

就是我们的最优策略。为什么只需要一步搜索就行呢？因为 $v_*$ 已经考虑未来可能行为的回报。

已知 $q_{*}$

已知 $q_*$ 就更直接了，只要取其中最大值对应的动作就是最优动作（策略）

\[\pi_*(a\vert s) \leftarrow \mathop{\text{argmax}}\limits_a\; q_*(s,a)\]

可以看到，如果已经得到了所有状态（或状态-动作）的最优价值函数，那么最优策略是很容易得到的。经过前面的分析我们指导，最优的状态（或状态-动作）价值函数可以通过对贝尔曼最优方程迭代来求解。具体来说，我们需要将强化学习分为两步，第一步解决一个预测问题，即给定状态、动作、奖励、状态转移概率，策略，预测出所有状态（或状态-动作）价值函数；第二步解决一个控制问题，即在预测问题的基础上，如何更新策略使得策略逐渐变得更优。

当状态转移概率（也即环境 $p$）已知时，预测问题可以通过 策略迭代（policy iteration） 或者 值迭代（value iteration） 的方式来先进行价值预测，再求解最优策略。这就是 动态规划方法（Dynamic Programming，DP）。

当状态转移概率（也即环境 $p$）未知时，可以通过 蒙特卡洛方法（Monte Carlo，MC） 进行价值预测。

4.7. 贝尔曼期望方程

从状态价值函数的定义出发

\[v_\pi(s) = \mathbb{E}[R+\gamma G\vert S=s] = \mathbb{E}[R\vert S=s] + \gamma \mathbb{E}[G\vert S=s], \;s\in S\]

其中

\[\mathbb{E}[G\vert S=s] = \sum_a\pi(a\vert s)\sum_{s^\prime}p(s^\prime\vert s,a)v_\pi(s^\prime) = \mathbb{E}[v_\pi(s^\prime)\vert S=s]\]

带回状态价值函数定义式，有

\[v_\pi(s) = \mathbb{E}[R+\gamma v_\pi(s^\prime)\vert S=s], \;\forall s\]

类似地，针对状态-动作价值函数，也有

\[q_\pi(s,a) = \mathbb{E}[R+\gamma q_\pi(s^\prime,a^\prime)\vert S=s,A=a],\; \forall s,a\]

上述两个公式合称为贝尔曼期望方程。

5. 参考文献

[1] 知乎. 强化学习（Reinforcement Learning）.

[2] ReEchooo. 强化学习知识要点与编程实践（1）——马尔可夫决策过程

[3] ReEchooo. 强化学习笔记（2）——马尔可夫决策过程

[4] Ping2021. 第二讲马尔可夫决策过程

[5] 木头人puppet. 强化学习：贝尔曼方程和最优性

[6] koch. 强化学习-贝尔曼方程和贝尔曼最优方程的推导

[7] Alvin. 知乎：3.6 最优策略和最优值函数