本文介绍了强化学习的 model-free 方法——蒙特卡洛法。
1. 引言
在前面介绍的动态规划方法中,我们假设已知模型的动态特性 $p(s^\prime,r \vert s,a)$,此时可以对下一步的状态和回报做出预测。而在很多实际案例中,我们无法得知模型的动态特性,此时动态规划方法就不适用了。注意到动态规划方法中的核心是对两类最优价值函数的估计,而当模型的动态特性未知时,我们不能通过迭代的形式计算最优价值函数,只能回归至价值函数原本的定义(期望),那么有什么办法对期望进行估计呢?这就是本章介绍的蒙特卡洛法,其通过大数定律保证在经过足够次数的采样后,可以通过求取价值函数的均值来逼近其期望。
2. 蒙特卡洛法
2.1. 大数定律与蒙特卡洛思想
大数定律:对于随机样本 $X$,假设 ${x_j}_{j=1}^N$ 是独立同分布(independent and identically distributed, iid)随机变量样本集,定义
\[\bar{x} = \frac{1}{N}\sum_{j=1}^N x_j\]为样本集的均值,那么
\[\begin{aligned} \mathbb{E}[\bar{x}] &= \mathbb{E}[X]\\ Var[\bar{x}] &= \frac{1}{N}Var[X] \end{aligned}\]当 $N\rightarrow \infty$ 时,方差趋于零,此时样本均值收敛至期望值。
大数定律表明,当随机事件发生的次数足够多时,随机事件发生的频率趋近于预期的概率。可以简单理解为样本数量越多,其平概率越接近于期望值。大数定律生效的前提条件是:1、独立重复事件;2、重复次数足够多。
蒙特卡洛法(Monte Carlo)方法,又称随机抽样或统计试验方法,思想是“当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。是一种基于大数定律的统计方法。
这一方法诞生于上世纪40年代美国的”曼哈顿计划”,名字来源于赌城蒙特卡罗(Monte Carlo)——位于法国的国中之国摩纳哥的一个以赌博业闻名的城市。而赌博象征概率;蒙特卡罗方法正是以概率为基础的方法,属于非确定性算法。
蒙特卡洛方法解决强化问题的本质,是基于通过采样大量数据来进行学习的经验方法实现的,因此,即便是在环境模型 $p(s^\prime,r \vert s,a)$ 未知/未完全可知的情况下,采用时间步骤有限的、完整序列(episode)中进行采样,并通过平均采样回报来解决强化学习问题。
2.2. 蒙特卡洛基础算法
2.2.1. 蒙特卡洛采样
在一次交互过程中,从特定的状态-动作($s_0, a_0$)出发,可采样得到一条序列
\[s_0, a_0, r_1, s_1, a_1, r_2, s_2,\cdots\]计算对应的回报
\[G_t = \sum_{k=0} \gamma^k R^{t+k+1}\]2.2.2. 蒙特卡洛价值估计
采集 $N$ 条序列,对于其中每条序列都算出回报后,对于首次或每次命中给定状态 $s_0$ 的轨迹,根据大数定律计算状态价值函数为
\[v_\pi(s_0) \doteq \mathbb{E}_\pi[G_t \vert S_t = s] =\frac{1}{N}\sum_{i=1}^N G_t^{(i)}\]同理,对于首次或每次命中($s_0,a_0$)的轨迹,根据大数定律计算状态-动作价值函数为
\[q_\pi(s_0, a_0) \doteq \mathbb{E}_\pi[G_t \vert S_t = s_0, A_t = a_0] =\frac{1}{N}\sum_{i=1}^N G_t^{(i)}\]在实际中,计算状态-动作价值函数的意义更大,方便策略改进。但注意,状态序列采样时需要同时命中 $S_t=s,A_t = a$ 条件时才能采集对应的 $G_t$,这对样本量需求更大,操作难度更高。
2.2.3. 算法流程
在策略迭代的基础上,给定出示策略 $\pi_0$,对于第 $k$ 次迭代,蒙特卡洛基础算法如下:
- 策略评估:对于所有的 $(s, a)$ 都需要进行足够多次的采样(二重循环遍历),采样得到足够多次的回合后计算首次或每次命中对应的 $G_t$,根据大数定律,$G_t$ 的均值可用来近似状态-动作价值函数 $q_{\pi_k}(s,a)$;
- 策略迭代:求解 $\pi_{k+1}(s) = \arg\max_{\pi}\sum_a \pi(a \vert s) q_{\pi_k}(s,a)$,最优策略是贪心策略,即只有当 $a_k^\star = \arg\max q_{\pi_k}(s \vert a)$ 时 $\pi_{k+1}(a_k^\star\vert s) = 1$。
可以看出,与策略迭代方法相比,蒙特卡洛基础算法直接估计状态-动作价值函数 $q_\pi(s,a)$ 并用于改进策略,而不依赖于(也没办法)先迭代求解 $v_\pi(s)$ 再计算 $q_\pi(s,a)$。
最后,蒙特卡洛方法的收敛性保证依赖于策略评估的收敛性的,因为蒙特卡洛方法仅仅将其中策略评估部分中价值函数的计算改为大数定律保证的采样估计。
蒙特卡洛基础算法的局限性:
-
对 $G_t$ 采样的过程中,样本必须在一幕(从 $t$ 时刻开始,$T$ 时刻结束)全部执行结束的状态下,才能获取 $R_{t+1},R_{t+2},…,R_{t+T}$ 的具体结果,并最终获得1个 $G_t$ 结果,采样数据利用率低。
-
最终需要获取足够量的($N$ 个) $G_t$ 结果才能够执行均值操作,整个过程绝大部分时间浪费在了采样过程,时间利用率低。
2.3. 蒙特卡洛改进算法(MC Exploring Starts)
2.3.1. 首次访问与每次访问
在蒙特卡洛基础算法中,我们假设序列是由给定的状态动作对 $(s_0, a_0)$ 开始采样得到的。注意到,同样的状态动作对除了首次出现外,也可能在后续采样过程中出现多次。以下面的一次采样序列为例,其中 $(s_0, a_0)$ 命中了两次
\[\textcolor{red}{s_0 \mathop{\rightarrow}\limits^{a_0}} s_1\mathop{\rightarrow}\limits^{a_4} \textcolor{red}{s_0 \mathop{\rightarrow}\limits^{a_0}} s_1 \mathop{\rightarrow}\limits^{a_2} s_5\mathop{\rightarrow}\limits^{a_3}\cdots\]因此计算回报的方式也分为以下两种:
-
首次访问型(first visit):只采集第一个出现($s_0,a_0$)时对应的 $G_t$(蒙特卡洛基础算法)
-
每次访问型(every visit):采集每次出现($s_0, a_0$)时对应的 $G_t$
首次访问型的优势与每次访问型的劣势:
- 采样序列与序列之间相互独立,首次访问型产生的回报样本同样也是经过独立试验产生的相互独立的样本;
- 相比之下,每次访问型中,后续回报计算只是首次回报的子集,回报计算之间是存在依赖的(非独立),当然如果两次访问之间距离很远则依赖也很弱;
首次访问型的劣势与每次访问型的优势:
- 首次访问型只能从一个采样序列中获取一个回报,数据利用率很低;
- 相比之下,每次访问型可能仅需要更少的序列数量就可以得到足够多的样本,数据利用率高;
2.3.2. 序列拆分与重复利用
更进一步,观察分析上述采样序列
\[\begin{aligned} \textcolor{red}{s_0 \mathop{\rightarrow}\limits^{a_0}} s_1\mathop{\rightarrow}\limits^{a_4} \textcolor{red}{s_0 \mathop{\rightarrow}\limits^{a_0}} s_1 \mathop{\rightarrow}\limits^{a_2} s_5\mathop{\rightarrow}\limits^{a_3}\cdots &\Rightarrow G_t(s_0, a_0) \times 2\\ \textcolor{blue}{s_1\mathop{\rightarrow}\limits^{a_4}} s_0 \mathop{\rightarrow}\limits^{a_0} s_1 \mathop{\rightarrow}\limits^{a_2} s_5\mathop{\rightarrow}\limits^{a_3}\cdots &\Rightarrow G_t(s_1, a_4)\\ \textcolor{blue}{s_1 \mathop{\rightarrow}\limits^{a_2}} s_5\mathop{\rightarrow}\limits^{a_3}\cdots &\Rightarrow G_t(s_1, a_2)\\ \textcolor{blue}{s_5\mathop{\rightarrow}\limits^{a_3}} \cdots &\Rightarrow G_t(s_5, a_3)\\ \end{aligned}\]可以发现,除了状态动作对 $(s_0, a_0)$ 可以计算其对应的回报外,同一条采样序列还可以用来计算很多其他状态动作对的回报,这种操作可以极大提高数据的利用效率。
2.3.3. 探索起点(Exploring Starts)
即使用到了序列拆分,上述过程依然存在某种弊端。注意到序列依然是指定特定的状态动作对作为起始点的,且随着迭代进进行,中间会有一些状态动作对的价值函数 $q(s,a)$ 取值变低。又因为因为策略迭代算法的策略改进过程是采取贪婪策略来选取动作的,这样会导致某些状态 $s$ 对应的低价值动作 $a$ 永远无法被采样选中,最终使得其状态-动作价值函数 $q(s,a)$ 无法得到更新,不利于策略改进。
因此,每次采样前不指定特定状态动作,而是以相同的概率随机选择初始的状态动作,可以保证每一个状态-动作对都能得到更新。再结合前述两项改进(每次访问、序列拆分),最终得到改进的蒙特卡洛方法,又被统称为 MC Exploring Starts。
为何方法命名为 Exploring Starts 而不提 Visit?以下为猜测分析: 首先明确,理论上能够保证寻找到最优策略的前提是所有的状态动作对都要能够被探索到,这可以通过两种方式实现
- 探索起点(随机初始化):每次采样时,随机选择一个状态动作对作为起始点,可保证所有状态动作对都有概率被选中;
- 每次访问:在采样序列中提高数据利用率,只能寄希望于当前策略下能够采样到所有状态动作对;
很显然,第二种方式在遍历状态动作对上是更加不确定的,因为其本质是提高数据利用效率,采样过程还是遵循贪婪策略,无法保证状态动作对一定有概率被采样到。因此,只能采取更加直接的第一种方式来命名,而只把第二种方式作为提高数据使用效率的技巧。
实际算法流程中,我们采用 从后往前的倒序 进行迭代计算,并引入增量更新(下一节介绍)的技巧,进一步提高计算效率,即
1
2
3
4
5
6
7
8
9
Sample an episode of length T by randomly select a starting state-action pair as the starting point
Initialize Gt = 0
for each step of episode, t = T-1, ..., 0, do:
(=== policy evaluation ===)
Gt = γ*Gt + r
N(st,at) = N(st,at) + 1
Q(st,at) = Q(st,at) + (Gt - Q(st,at)) / N(st,at)
(=== policy improvement ===)
π(a|st) = 1 if a = argmax Q(st,a), π(a|st) = 0 otherwise
2.3.4. 增量更新(incremental update)
不论是蒙特卡洛基础算法还是其改进算法(MC Exploring Starts),计算回报 $G_t$ 时都需要采样足够多次数($N$ 次)后才能保证计算得到的均值比较接近价值函数的期望。在实际计算中,我们可以使用增量更新技巧提高计算均值的效率。
计算均值的增量更新示例: 已知一个数列中包含3个数值 $[3,4,5]$,当采样两次,第一次采到3、第二次采到4时,前后两次计算的均值为
\[\begin{aligned} \text{(use 1{st} sample)}\; u_1 &= \frac{1}{1}\sum_{i=1}^1 x_i = 3\\ \text{(use 1st+2nd sample)}\; u_2 &= \frac{1}{2}\sum_{i=1}^2 x_i = \frac{3+4}{2} = 3.5\\ \text{(use 1st+2nd+3rd sample)}\; u_3 &= \frac{1}{3}\sum_{i=1}^3 x_i = \frac{3+4+5}{2} = 3.5\\ \end{aligned}\]可以将均计算式改写成如下形式的迭代形式,每一次迭代只需要用到上次计算的均值,而不需要用到所有历史样本值
\[\begin{aligned} \text{(use last average(u1) + current(x2))}\;u_2 &= u_1-\frac{1}{2}(u_1-x_2) = 3+\frac{1}{2} = 3.5\\ \text{(use last average(u2) + current(x3))}\;u_3 &= u_2-\frac{1}{3}(u_2-x_3) = 3.5+\frac{1}{2} = 4 \end{aligned}\]
蒙特卡洛增量更新方法如下
\[\begin{cases} N &\leftarrow N+1\\ G(S_t) &\leftarrow G(S_t) - \frac{1}{N} (G(S_t) - G_t) \end{cases}\]这样只需要每次得到 1个 新的 $G_t$ 即可更新一次回报均值 $G(S_t)$(也即价值函数的估计),即便和期望存在差异,但更新时间更短,更容易观察到收敛结果,且可以随着时间的推移逐步接近均值(在后续时序差分法中详细介绍)。
更进一步,我们可以每次迭代都需要变化的 $\frac{1}{N}$,改为用一个常数小量 $\alpha$ 来代替,即
\[G(s_t) = G(s_t) - \alpha (G(s_t) - G_t)\]在后续介绍随机近似理论和时序差分法中,我们通过 RM 算法的收敛性来保证上述增量更新形式是收敛的。
2.4. 蒙特卡洛改进算法(MC e-greedy)
2.4.1. 探索和利用
虽然探索起点(Exploring Starts)理论上可以保证每个状态动作对都有概率被采样到,但实际中很难实现,特别在一些需要与物理系统进行交互的应用中,有些状态动作可能很难作为初始状态进行设置。
前面在探索起点的章节中我们介绍过,通过每次访问仍然无法保证所有状态动作对都有概率被采样到,因为他本质上还是遵循贪婪策略,所以无法保证所有状态动作对都能被采样到。那如果我们不采用贪婪策略这么极端的呢?
事实上,我们可以设计一种 $\varepsilon$-greedy 策略,即在每次访问时,在大概率选到贪婪动作的同时,以某个较小概率随机选择一个动作。在这个策略下,随着采样序列的变长和采样次数的增多,所有状态动作对都有概率被采样到,也就达到了我们的目标。
$\varepsilon$-greedy 策略可数学表示如下
\[\pi(a|s) = \begin{cases} 1-\frac{\varepsilon}{\vert A \vert}(\vert A \vert-1)= \frac{\varepsilon}{\vert A \vert} + 1-\varepsilon & \text{if } a = \arg\max_a Q(s,a)\\ \frac{\varepsilon}{\vert A \vert} & \text{other }\vert A \vert-1\text{ actions} \end{cases}\]其中 $\varepsilon\in[0,1]$,$\vert A \vert$ 表示当前状态下可选动作的个数。
上述策略平衡了 探索(exploration)和 利用(exploitation):
- 当 $\varepsilon = 0$ 时,策略完全贪婪,只选择当前价值函数下最优的动作,这样可以最大化利用已有的价值函数,但可能会错过一些未知的最优动作;
- 当 $\varepsilon = 1$ 时,策略完全随机(策略变成均匀分布,即每个动作的概率相同),这样可以最大化探索未知的动作,但可能会错过已知的最优动作。
采用 $\varepsilon$-greedy 策略的蒙特卡洛方法,称为 MC e-greedy。该方法不要求对起点进行探索了,只要在每次访问时,按照 $\varepsilon$-greedy 策略随机选择一个动作,就可以保证所有状态动作对都有概率被采样到,后面的探索性分析章节可以进一步佐证此结论。
2.4.2. 探索性分析
下面给出一个 $\varepsilon$-greedy 策略的探索能力与参数 $\varepsilon$ 的关系的极端案例。设置场景如下:
- 智能体从左上角状态采取特定动作出发;
- 智能体遇到终点不停止,而是继续前进,意味着持续采样 1 个 episode;
- 其他参数设置为:$r_{\text{boundary}}=-1,r_{\text{forbidden}}=-10,r_{\text{target}}=1,\gamma=0.9$。
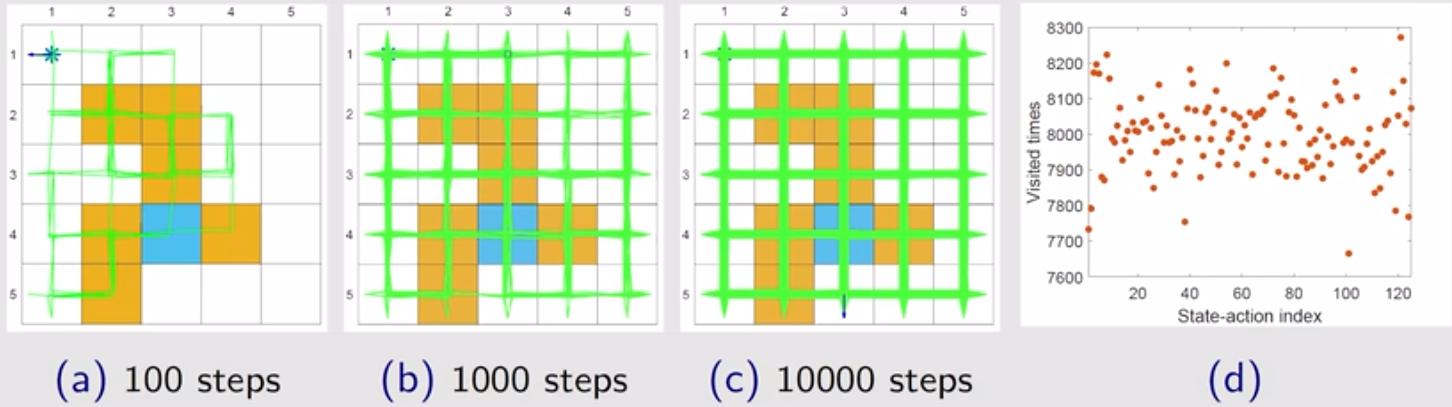
设置 $\varepsilon = 1$,即均匀随机选择动作,此时策略的探索能力最大。下图展示了探索 100 步(图(a))、探索 1000步(图(b))、探索 10000 步(图(c))的探索结果,可以看出在 1000 步时智能体已经采样到了绝大部分状态动作对。同时,图(d)展示了探索 100 万步后,所有 125 个状态动作对中每个状态动作对被访问的次数,次数相差不大,表明符合均匀随机选择动作的结果。
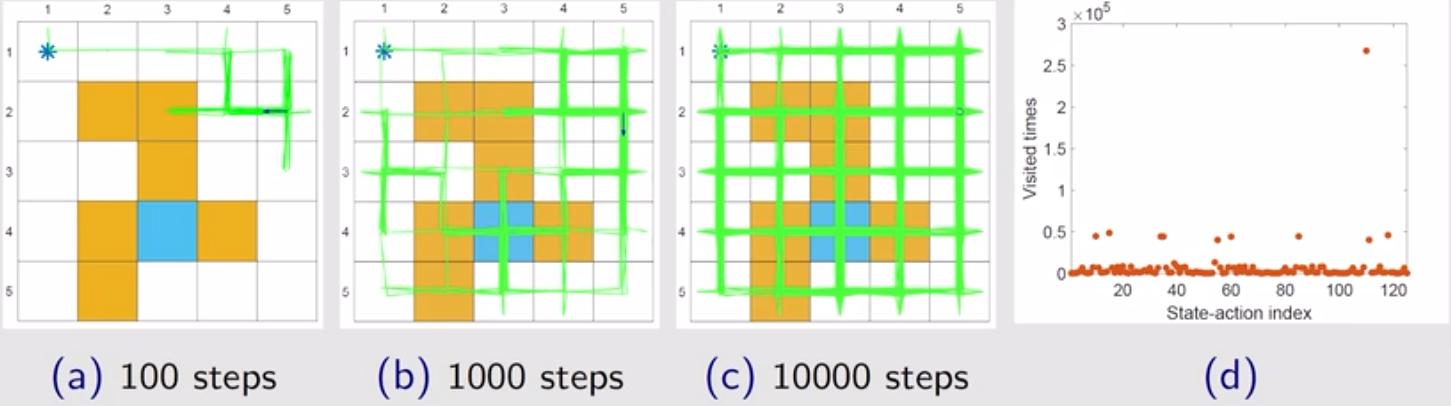
设置 $\varepsilon = 0.1$,相应结果如下图所示。上下对比可以看出: (1)对比图 (a) 和图 (b) 发现:同样采样至第 100/1000 步,智能体探索到的状态动作对远没有前面 $\varepsilon = 1$ 时的多; (2)对比图 (c) 发现:探索足够多的次数后,二者均能逐渐探索到所有状态动作对,只不过 $\varepsilon = 0.1$ 需要的步数更长,探索速度更慢; (3)对比图 (d) 发现:设置比较小的 $\varepsilon$,策略的探索能力会下降,有些较优的状态动作对可能会大量重复地被访问。 (4)虽然探索能力不如均匀随机选择动作($\varepsilon=1$),但其在步数足够长的时候,依然能够探索到所有状态动作对,相比贪婪策略,其探索能力依然更强。 (5)虽然($\varepsilon=1$)探索性更强,但也存在弊端,在后续最优性分析章节详细阐述。
至此可以给出一个**重要结论**,采用 $\varepsilon$-greedy 策略,不用随意初始化起点,也能保证所有状态动作对都可以被采样到。这在实际使用时非常有意义,因为他可以避免设置一些在与实际物理系统交互过程中难以稳定保持的状态(或状态动作对)作为起点,降低了对探索起点设置的门槛。比如:
- 复杂游戏的关卡开头是固定的,而中间状态千差万别,难以随意设置中间状态作为起点;
- 某些被控系统都是以相同的状态开机,但中间运行过程根本无法暂停用于初始化;
$\varepsilon$-greedy 策略不但影响着 MC 方法,后续还进一步用于时序差分法(TD)和策略梯度法(PG)、乃至二者结合的 Actor-Critic 方法,影响十分深远。
2.4.3. 最优性分析
在实际应用中,我们会在采用 $\varepsilon$-greedy 策略训练完毕得到策略后,将其转为贪婪策略使用。因此有必要分析上述转换得到的贪婪策略是否为理论上的最优策略。或者换句话说,设置的 $\varepsilon$ 对策略的最优性有什么影响。
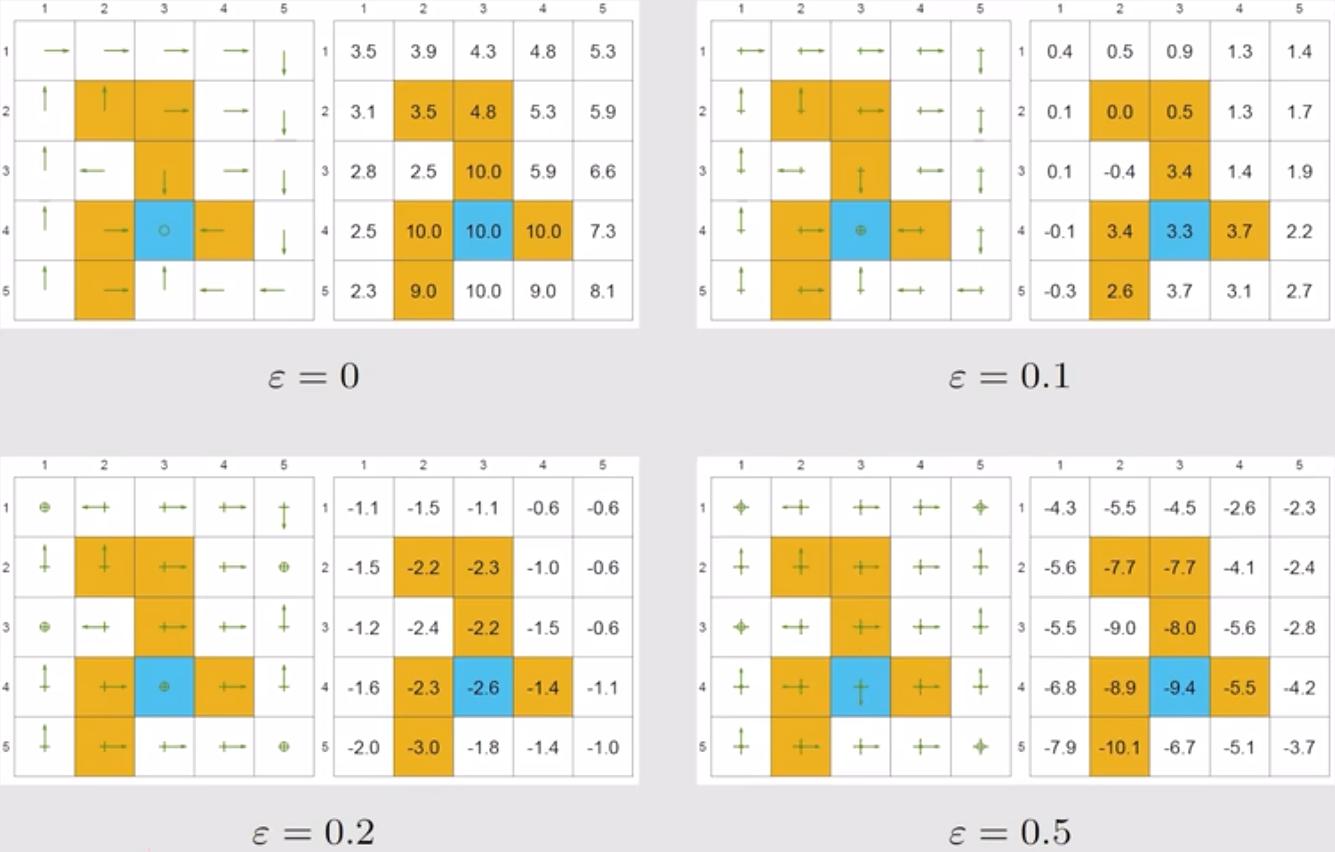
针对上述同样的 Grid world 场景,在其他参数相同的条件下($r_{\text{boundary}}=-1,r_{\text{forbidden}}=-10,r_{\text{target}}=1,\gamma=0.9$),分别设置$ \varepsilon = 0, 0.1, 0.2, 0.3$,分析计算得到的策略与最优策略的关系,如下图所示。图中一共有四组参数取值对应的子图,每组子图的左侧为策略,右侧为对应的状态价值函数。
- 当 $\varepsilon = 0$ 时(左上图),其退化为贪婪策略,其价值函数和策略都是最优策略,最优性是由策略迭代的收敛性保证的;
- 当 $\varepsilon = 0.1$ 时(右上图),得到的策略和最优策略的依然是一致的,但状态价值函数已经偏离了最优值;
- 随着 $\varepsilon$ 的增加,得到的策略逐渐变差,价值函数也急剧偏离最优价值函数。
当 $\varepsilon$ 较大时,一个典型的情形是,终点的价值函数居然是一个十分大的负数,这显然违背逻辑(在贝尔曼方程中终点价值函数肯定是最大的),这是因为在抵达终点后,其上方和左右都是陷阱区域,采用较大 $\varepsilon$ 取值的 $\varepsilon$-greedy 策略会频繁进入到这些区域(选择了较差的动作),导致获得较多负奖励,这使得策略评估该状态的价值很低。因此,$\varepsilon$-greedy 策略通过牺牲最优性来提高探索性。
上述分析给了我们设置参数 $\varepsilon$ 的重要启示:
- 在算法训练的早期阶段,可以设置较大的 $\varepsilon$ 以提高探索快速性;
- 随着算法训练过程的持续,应当逐渐减小 $\varepsilon$ 的取值以保证近似最优性。
2.5. 蒙特卡洛的局限性
虽然蒙特卡洛方法及其各种改进方法已经能够较好克服各种缺点,实现在无模型条件下的强化学习,但其仍然要求采样一条完整的序列直到结束时刻 $T$ 才能以 倒序 的形式计算出回报 $G_t$。如果采样可以无限进行下去而无法停止,就根本无法计算出回报,更别提策略改进了。因此,我们还需要继续寻找可行的方法实现无模型强化学习,这就是后面介绍时序差分法(Temporal Difference,TD)。
3. 参考文献
[1] shuhuai008. bilibili蒙特卡洛方法-强化学习-合集
[2] 韵尘. 知乎:5.1 —— 蒙特卡洛预测(Monte Carlo Prediction)
[3] 静静的喝酒. 强化学习之SARSA