MAML 是2017年 Chelsea Finn 大佬提出的一种基于优化(Optimized-based)的小样本学习方法,核心在两个不同的数据集中分别计算梯度和更新参数。
1. MAML
2017.《Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks》
The key idea underlying our method is to train the model’s initial parameters such that the model has maximal performance on a new task after the parameters have been updated through one or more gradient steps computed with a small amount of data from that new task.
本文的设想是训练一组初始化参数,通过在初始参数的基础上进行一或多步的梯度调整,来达到仅用少量数据就能快速适应新task的目的。为了达到这一目的,训练模型需要最大化新task的loss function的参数敏感度(maximizing the sensitivity of the loss functions of new tasks with respect to the parameters),当敏感度提高时,极小的参数(参数量)变化也可以对模型带来较大的改进。本文提出的算法可以适用于多个领域,包括少样本的回归、图像分类,以及增强学习,并且使用更少的参数量达到了当时(2017年)最先进的专注于少样本分类领域的网络的准确率。
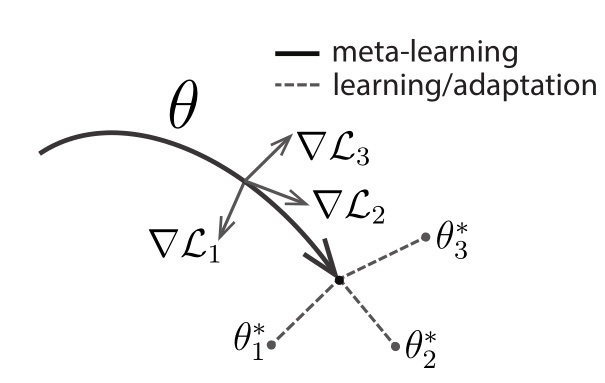
核心算法示意图如下
如上图所示,作者便将目标设定为,通过梯度迭代,找到对于task敏感的参数 $\theta$ 。训练完成后的模型具有对新task的学习域分布最敏感的参数,因此可以在仅一或多次的梯度迭代中获得最符合新任务的 $\theta^*$ ,达到较高的准确率。
1.1. 算法
假设这样一个监督分类场景,目的是训练一个数学模型 $M_{fine-tune}$ ,对未知标签的图片做分类,则两大步骤如下:
- 利用某一批数据集训练元模型 $M_{meta}$
- 在另外一批数据集上精调(fine-tune)得到最终的模型 $M_{fine-tune}$ 。
MAML在监督分类中的算法伪代码如下:
该算法是 meta-train 阶段,目的是得到 $M_{meta}$。下面进行详细分析:
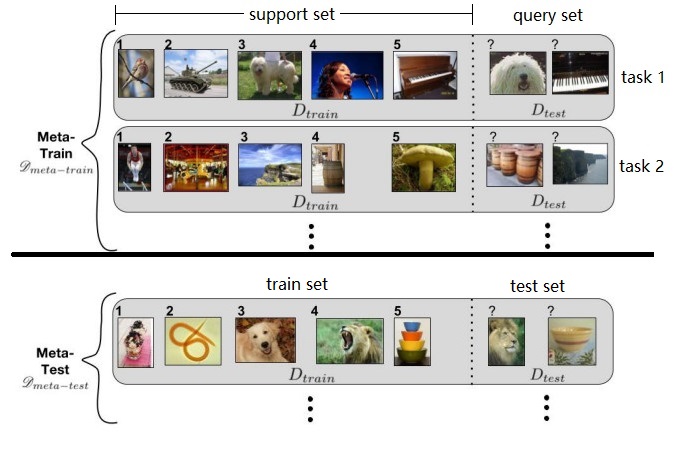
参考示意图如下,一个 task 表示为 $\mathcal T$
第一个Require,假设我们有一个很大的图像池,里面有很多很多类别的图像,每类图像有几十个。我们从中随机抽取五个类别,形成一个 task $\mathcal T$,如此反复随机抽取可以得到一批(e.g. 1000个)task 作为训练集 $p(\mathcal T)$。假设一个 $\mathcal T$ 包含5类,每类20个样本,随机选5样本作为support set,剩余15样本为query set。
训练样本就这么多,要组合形成那么多的task,岂不是不同task之间会存在样本的重复?或者某些task的query set会成为其他task的support set?没错!就是这样!我们要记住,MAML的目的,在于fast adaptation,即通过对大量task的学习,获得足够强的泛化能力,从而面对新的、从未见过的task时,通过fine-tune就可以快速拟合。task之间,只要存在一定的差异即可。
第二个Require,step size 就是学习率,MAML 是基于二重梯度(gradient by gradient),每次迭代有两次参数更新过程,所以有两个学习率可以调整。
1:随机初始化模型参数 $\theta$;
2:循环,对于每个epoch,进行若干batch;
3:随机选取若干个(比如4个) $\mathcal T$ 形成一个batch;
4:对于每个batch中的第 $i$ 个 $\mathcal T$ ,进行第一次梯度更新「inner-loop 内层循环」。
5:选取 $\mathcal T_i$ 中的 support set,共 $N\cdot K$个样本(5-way 5-shot=25个样本)
6:计算每个参数的梯度。原文写对每一个类下的 $K$ 个样本做计算。实际上参与计算的总计有 $N\cdot K$ 个样本。这里的loss计算方法,在回归问题中就是MSE;在分类问题中就是cross-entropy;
7:进行第一次梯度更新得到 $\theta’$,可以理解为对 $\mathcal T_i$ 复制一个原模型 $f(\theta)$ 来更新参数;
8:挑出训练集中的 query set 数据用于后续二次梯度更新;
9:完成第一次梯度更新。
10:进行第二次梯度更新,此时计算出的梯度直接通过GD作用于原模型上,用于更新其参数。「outer-loop 外层循环」
大致与步骤 7 相同,但是不同点有三处:
-
隐含了二重梯度,需要计算 $\mathcal L_{T_i}f(\theta’)$ 对 $\theta$ 的导数,而 $\mathcal L_{T_i}f(\theta’)$ 是 $\theta’$ 的函数, $\theta’$ 又是 $\theta$ 的函数(见步骤7);
-
不再分别利用每个 $\mathcal T$ 的loss更新梯度,而是计算一个 batch 中模型 $L_{T_i}f(\theta’)$ 的 loss 总和进行梯度下降;
-
参与计算的样本是task中的 query set(5way*15=75个样本),目的是增强模型在task上的泛化能力,避免过拟合support set。
11:结束在该batch中的训练,回到步骤3,继续采样下一个batch。
总结:MAML使用训练集优化内层循环,使用测试集优化模型,也就是外层循环。外层循环需要计算二重梯度(gradient by gradient)。
1.2. 梯度下降数学分析
定义神经网络模型的初始的参数为
\[\boldsymbol{\theta} = [\theta_1,\theta_2,...,\theta_n]^T\]假设随机选取的一批任务为 $\tau$,包含 10 个样本,每个样本输入 6 个量,输出 4 个量。神经网络即为一个 6 输入 2 输出的网络。
样本输入矩阵为(行是样本,列是输入维度)
\[\boldsymbol M_{in} = \begin{bmatrix} ^1x_1& ^1x_2& \cdots& ^1x_6\\ ^2x_1& ^2x_2& \cdots& ^2x_6 \\ \vdots& \vdots & \ddots & \vdots\\ ^{10}x_1& ^{10}x_2& \cdots& ^{10}x_6 \end{bmatrix}\]同理,输出矩阵为
\[\boldsymbol M_{out} = \begin{bmatrix} ^1y_1& ^1y_2& \cdots& ^1y_4\\ ^2y_1& ^2y_2& \cdots& ^2y_4 \\ \vdots& \vdots & \ddots & \vdots\\ ^{10}y_1& ^{10}y_2& \cdots& ^{10}y_4 \end{bmatrix}\]对于参数为 $\boldsymbol \theta$ 的模型,其预测输出矩阵为
\[\boldsymbol M_{pred}(\boldsymbol \theta) = \begin{bmatrix} ^1\hat{y}_1(\boldsymbol \theta)& ^1\hat{y}_2(\boldsymbol \theta)& \cdots& ^1\hat{y}_4(\boldsymbol \theta)\\ ^2\hat{y}_1(\boldsymbol \theta)& ^2\hat{y}_2(\boldsymbol \theta)& \cdots& ^2\hat{y}_4(\boldsymbol \theta) \\ \vdots& \vdots & \ddots & \vdots\\ ^{10}\hat{y}_1(\boldsymbol \theta)& ^{10}\hat{y}_2(\boldsymbol \theta)& \cdots& ^{10}\hat{y}_4(\boldsymbol \theta) \end{bmatrix}\]定义一个损失函数 $L_\tau$ 来衡量模型在任务 $\tau$ 上的性能(即模型预测输出与期望输出间的距离),可以采用 MSE 来表征,注意到损失函数是关于模型参数的函数
\[L_\tau(\boldsymbol \theta) = MSE_\tau = \frac{1}{10\cdot4} \cdot [\frac{1}{2} \sum_i^{10} \sum_j^{4}(^i\hat{y}_j(\boldsymbol \theta) - {}^iy_j)^2]\]如何使得模型的预测输出与期望输出的距离变小呢?按照梯度下降方法(GD),我们可以计算损失函数 $L_\tau(\boldsymbol \theta)$ 关于模型参数 $\boldsymbol \theta$ 的梯度,然后沿着这个梯度的负方向更新模型参数即可。
假设损失函数关于模型参数的梯度为 $\boldsymbol g$,则
\[\begin{aligned} \boldsymbol g = \nabla_{\boldsymbol \theta} L_\tau(\boldsymbol \theta) = \frac{\partial L_\tau(\boldsymbol \theta)}{\partial \boldsymbol \theta} = \begin{bmatrix} \partial L_\tau(\boldsymbol \theta) / \partial \theta_1\\ \partial L_\tau(\boldsymbol \theta) / \partial \theta_2\\ \vdots\\ \partial L_\tau(\boldsymbol \theta) / \partial \theta_n \end{bmatrix} \end{aligned}\]我们可以计算1次梯度下降,也可以计算多次。假设 $\boldsymbol g_1$ 是在原始模型参数上进行第1次梯度计算,有
\[\begin{aligned} \boldsymbol g_1 & = \nabla_{\boldsymbol \theta} L_\tau(\boldsymbol \theta_0)\\ \boldsymbol \theta_1 &= \boldsymbol \theta_0 - \alpha \boldsymbol g_1 \end{aligned}\]其中,$\boldsymbol \theta_1$ 表示经过1次梯度更新后的模型参数,后文以此类推。
第2次梯度计算建立在第1次梯度计算的基础上,有
\[\begin{aligned} \boldsymbol g_2 &= \nabla_{\boldsymbol \theta_1} L_\tau(\boldsymbol \theta_1)\\ \boldsymbol \theta_2 &= \boldsymbol \theta_1 - \alpha \boldsymbol g_2\\ & = \boldsymbol \theta_0 - \alpha \boldsymbol g_1 - \alpha \boldsymbol g_2 \end{aligned}\]我们将1次,2次,…,直到 $k$ 次梯度计算的过程统一列写如下:
\[\begin{aligned} initialization:\quad&\boldsymbol \theta_0 = \boldsymbol \theta\\ 1^{st}\;gradient\;step:\quad&\boldsymbol \theta_1 = U^1_\tau(\boldsymbol \theta)=\boldsymbol \theta - \alpha \boldsymbol g_1\\ 2^{nd}\;gradient\;step:\quad&\boldsymbol \theta_2 = U^2_\tau(\boldsymbol \theta)=\boldsymbol \theta- \alpha \boldsymbol g_1- \alpha \boldsymbol g_2\\ ...&...\\ k^{th}\;gradient\;step:\quad&\boldsymbol \theta_k = U^k_\tau(\boldsymbol \theta)=\boldsymbol \theta- \alpha \boldsymbol g_1- \alpha \boldsymbol g_2-...- \alpha \boldsymbol g_k\\ &\boldsymbol g_k = \nabla_{\boldsymbol \theta_{k-1}} L_\tau(\boldsymbol \theta_{k-1}) \end{aligned}\]其中,模型参数 ${}^k_\tau\boldsymbol \theta$ 表示模型参数已经在任务数据 $\tau$ 上经过 $k$ 次更新,$U^k_\tau$ 是一个梯度算子,定义为在数据 $\tau$ 进行 $k$ 次更新,$U^k_\tau(\boldsymbol \theta)={}^{k}_\tau \boldsymbol \theta$。
1.3. 基于优化的元学习目标
MAML 的目标是:找寻一组模型初始参数 $\boldsymbol \theta$,使得模型在面对随机选取的新任务 $\tau$ 时,经过 $k$ 次梯度更新,在 $\tau$ 上的损失函数就能达到很小。
We consider the optimization problem of MAML: find an initial set of parameters, $\boldsymbol \theta$, such that for a randomly sampled task $\tau$ with corresponding loss $L_\tau$, the learner will have low loss after $k$ updates. ——–[Reptile]
用数学语言描述,即
\[\begin{aligned} \mathop{minimize}_{\theta} \; \mathbb E_{\tau}[L_{\tau}(^{k}_\tau\boldsymbol \theta)] = \mathop{minimize}_{\theta} \; \mathbb E_{\tau}[L_{\tau}(U^k_\tau(\boldsymbol \theta))] \end{aligned}\]其中,${}^{k}_\tau \boldsymbol \theta$ 是在任务 $\tau$ 上经过 $k$ 次更新后的模型参数。在前面的梯度数学分析中,我们省略了下标 $\tau$,因为梯度计算和损失函数计算默认都是对同一批数据,但是在这里加上下标,是因为后面 MAML 并不在同一批数据上计算梯度和计算损失函数,需要下标做区分。
这里说的是 MAML 的目标,是因为截至 MAML 文章发表,人们还没有建立起元学习的框架概念,后来人们将 MAML 等寻找最优模型初始参数的方法称作 基于优化的元学习问题(Optimization-based Meta-Learning)的方法,上述数学描述也就成为整个问题的共同目标。
1.4. MAML数学分析
假设任务 $\tau$ 可以分解为两个互不相交的数据子集 A(比如包含7个样本) 和 B(包含3个样本),MAML 通过进行 $k=1$ 次梯度算子更新,将上述问题转化为如下问题。省略 $U$ 的上标 $k$,有
\[\begin{aligned} \mathop{minimize}_{\theta} \; \mathbb E_{\tau}[L_{B}(U_{A}(\boldsymbol \theta))] \end{aligned}\]即 MAML 在数据集 A 上训练,在数据集 B 上计算损失函数 $L_{B}(U_{A}(\boldsymbol \theta))$,使得其最小。
MAML 中只进行 $k=1$ 次梯度算子更新,作者号称有如下四个原因:
-
Meta Learning会快很多;
-
如果能让模型只经过一次梯度下降就性能优秀,当然很好;
-
Few-shot learning的数据有限,多次梯度下降很容易过拟合;
-
刚才说的可以在实际应用中多次梯度下降。
为了使损失函数最小,需要计算损失函数对模型原始参数 $\boldsymbol \theta$ 的梯度 $\boldsymbol g_{MAML}$,然后在梯度负方向更新参数。 即
\[\boldsymbol g_{MAML} = \nabla_{\boldsymbol \theta} L_{B}(U_{A}(\boldsymbol \theta))\]注意到
\[U^{k=1}_\tau(\boldsymbol \theta)={}\tau \boldsymbol \theta_1\]省略 $k$,那么
\[\begin{aligned} \boldsymbol g_{MAML} &= \nabla_{\boldsymbol \theta} L_{B}(U_{A}(\boldsymbol \theta))= \frac{\partial}{\partial \boldsymbol \theta} L_{B}(U_{A}(\boldsymbol \theta))\\ &= L_{B}'({}_{A}\boldsymbol \theta_1) U_{A}'(\boldsymbol \theta)\quad where \quad {}_{A} \boldsymbol \theta_1 = U_{A}(\boldsymbol \theta) \end{aligned}\]上式中,第一项是使用 A 数据进行一次梯度更新后的模型参数计算损失函数,然后在 B 数据上计算损失函数的导数,这里的导数是对更新后的模型参数求的,因此这一项比较好求。
下面计算第二项 $U’_{A}(\boldsymbol \theta)$。前面算子更新时我们知道
\[U^1_\tau(\boldsymbol \theta)=\boldsymbol \theta - \alpha \boldsymbol g_1\]那么有
\[U_{A}'(\boldsymbol \theta) = \frac{\partial U_{A}(\boldsymbol \theta)}{\partial \boldsymbol \theta}= \frac{\partial \boldsymbol \theta}{\partial \boldsymbol \theta}-\alpha \frac{\partial \boldsymbol g_1}{\partial \boldsymbol \theta}\]下面分析第一项 $\frac{\partial \boldsymbol \theta}{\partial \boldsymbol \theta}$ 的展开,注意到 $\boldsymbol \theta = [\theta_1,\theta_2,…,\theta_n]^T$ 的定义,那么该项展开即为 $\boldsymbol \theta$ 的每个分量对其自身求偏导,需要分情况讨论
\[\begin{aligned} \frac{\partial \theta_i}{\partial \theta_j} = \left\{\begin{matrix} 1 \quad i=j\\ 0 \quad i \neq j \end{matrix}\right. \end{aligned}\]那么第一项即为 $n\times n$ 单位阵(可以看作一个特殊的 Jacobian 矩阵)
\[\begin{aligned} \frac{\partial \boldsymbol \theta}{\partial \boldsymbol \theta} = \begin{bmatrix} 1\;0\;\cdots \; 0\\ 0\;1\;\cdots \; 0\\ \vdots\;\vdots\;\ddots \; \vdots\\ 0\;0\;\cdots \; 1 \end{bmatrix} = \boldsymbol I_{n \times n} \end{aligned}\]然后分析第二项的展开。根据前文知
\[\begin{aligned} \boldsymbol g_1 = \frac{\partial L_\tau(\boldsymbol \theta)}{\partial \boldsymbol \theta} = \begin{bmatrix} \partial L_\tau(\boldsymbol \theta) / \partial \theta_1\\ \partial L_\tau(\boldsymbol \theta) / \partial \theta_2\\ \vdots\\ \partial L_\tau(\boldsymbol \theta) / \partial \theta_n \end{bmatrix} \end{aligned}\]代入第二项有
\[\begin{aligned} \alpha \frac{\partial \boldsymbol g_1}{\partial \boldsymbol \theta} &= \alpha \frac{\partial L_\tau(\boldsymbol \theta)}{\partial \boldsymbol \theta} / \partial \boldsymbol \theta\\ & = \alpha \begin{bmatrix} \partial L_\tau(\boldsymbol \theta) / \partial \theta_1\\ \partial L_\tau(\boldsymbol \theta) / \partial \theta_2\\ \vdots\\ \partial L_\tau(\boldsymbol \theta) / \partial \theta_n \end{bmatrix} / \partial \boldsymbol \theta\\ & = \alpha \begin{bmatrix} \partial (\frac{\partial L_{A}}{\partial \theta_1}) / \partial \theta_1 & \partial (\frac{\partial L_{A}}{\partial \theta_1}) / \partial \theta_2& \cdots & \partial (\frac{\partial L_{A}}{\partial \theta_1}) / \partial \theta_n \\ \partial (\frac{\partial L_{A}}{\partial \theta_2}) / \partial \theta_1 & \partial (\frac{\partial L_{A}}{\partial \theta_2}) / \partial \theta_2& \cdots & \partial (\frac{\partial L_{A}}{\partial \theta_2}) / \partial \theta_n \\ \vdots & \vdots & \ddots & \vdots\\ \partial (\frac{\partial L_{A}}{\partial \theta_n}) / \partial \theta_1 & \partial (\frac{\partial L_{A}}{\partial \theta_n}) / \partial \theta_2& \cdots & \partial (\frac{\partial L_{A}}{\partial \theta_n}) / \partial \theta_n \\ \end{bmatrix}_{n \times n}\\ &= \alpha \begin{bmatrix} \partial^2 L_{A} / \partial \theta_1^2 & \partial^2 L_{A} /\partial \theta_1 \partial \theta_2 & \cdots & \partial^2 L_{A} /\partial \theta_1 \partial \theta_n \\ \partial^2 L_{A} /\partial \theta_2 \partial \theta_1 & \partial^2 L_{A} / \partial \theta_2^2 & \cdots & \partial^2 L_{A} /\partial \theta_2 \partial \theta_n \\ \vdots & \vdots & \ddots & \vdots\\ \partial^2 L_{A} /\partial \theta_n \partial \theta_1 & \partial^2 L_{A} /\partial \theta_n \partial \theta_2& \cdots & \partial^2 L_{A} / \partial \theta_n^2 \\ \end{bmatrix}_{n \times n}\\ &= \alpha \boldsymbol H_{A}(\boldsymbol \theta)_{n \times n} \end{aligned}\](向量对向量求偏导,是向量的每个分量对另一个向量的每个分量求偏导后形成矩阵,就是Hessian 矩阵!Hessian 等价于梯度的 Jacobian 矩阵。——Ian Goodfellow所著的《Deep Learning》的P78)
最终计算得到的第二项 $U_{A}’(\boldsymbol \theta)$的表达式为
\[\begin{aligned} U_{A}'(\boldsymbol \theta) &= \frac{\partial U_{A}(\boldsymbol \theta)}{\partial \boldsymbol \theta}= \frac{\partial \boldsymbol \theta}{\partial \boldsymbol \theta}-\alpha \frac{\partial \boldsymbol g_1}{\partial \boldsymbol \theta}\\ &= \boldsymbol I_{n \times n} - \alpha \boldsymbol H_{A}(\boldsymbol \theta)_{n \times n} \end{aligned}\]MAML 的作者表示,大部分计算量都在于计算 $H_{A}(\boldsymbol \theta)_{n \times n}$ 这个包含二重梯度的 Hessian 矩阵,导致 MAML 的计算量很大,使得 MAML 以难以训练成名。
那么当进行 $k>1$ 次梯度算子更新时又会怎样呢?(作者:我不要面子的?)
我们将1次,2次,…,直到 $k$ 次梯度计算的过程改写如下(注意到这里采用数据集 A 来更新参数 $\boldsymbol\theta$,但是在式中我们省略了左下标 A):
\[\begin{aligned} initialization:\quad&\boldsymbol \theta_0 = \boldsymbol \theta\\ 1^{st}\;gradient\;step:\quad&\boldsymbol \theta_1 = U^1_A(\boldsymbol \theta)=\boldsymbol \theta_0 - \alpha \boldsymbol g_1\\ 2^{nd}\;gradient\;step:\quad&\boldsymbol \theta_2 = U^2_A(\boldsymbol \theta)=\boldsymbol \theta_1 - \alpha \boldsymbol g_2\\ ...&...\\ k^{th}\;gradient\;step:\quad&\boldsymbol \theta_k = U^k_A(\boldsymbol \theta)=\boldsymbol \theta_{k-1}- \alpha \boldsymbol g_k\\ &\boldsymbol g_k = \nabla_{\boldsymbol \theta_{k-1}} L_\tau(\boldsymbol \theta_{k-1}) \end{aligned}\]在外循环中,假设只使用一个task来更新参数,省略求和号,有
\[\boldsymbol \theta \leftarrow \boldsymbol \theta - \beta \cdot \boldsymbol g_{MAML}\]其中
\[\begin{aligned} \boldsymbol g_{MAML} &= \nabla_{\boldsymbol \theta} L_{B}(U^k_{A}(\boldsymbol \theta))\\ &= \nabla_{\boldsymbol \theta} L_{B}(\boldsymbol \theta_k)\\ &= \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k)\cdot(\nabla_{\boldsymbol \theta}\boldsymbol \theta_k)\\ &= \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k)\cdot(\nabla_{\boldsymbol \theta_{k-1}}\boldsymbol \theta_k) \cdots (\nabla_{\boldsymbol \theta_{1}}\boldsymbol \theta_2)\cdot (\nabla_{\boldsymbol \theta_{0}}\boldsymbol \theta_1)\\ &= \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k)\cdot\prod_{i=1}^k (\nabla_{\boldsymbol \theta_{i-1}}\boldsymbol \theta_i)\\ &= \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k)\cdot\prod_{i=1}^k (\nabla_{\boldsymbol \theta_{i-1}}(\boldsymbol \theta_{i-1}- \alpha \boldsymbol g_i))\\ &= \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k)\cdot\prod_{i=1}^k (\nabla_{\boldsymbol \theta_{i-1}}(\boldsymbol \theta_{i-1}- \alpha (\nabla_{\boldsymbol \theta_{i-1}} L_\tau(\boldsymbol \theta_{i-1})))\\ &= \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k)\cdot\prod_{i=1}^k (\boldsymbol I - \alpha \nabla_{\boldsymbol \theta_{i-1}} (\nabla_{\boldsymbol \theta_{i-1}} L_\tau(\boldsymbol \theta_{i-1})))\\ \end{aligned}\]当 $k=1$ 时我们发现,后面的连乘项就退化为前面已经推得的 Hessian 矩阵了
\[\begin{aligned} \prod_{i=1}^{k=1} (\boldsymbol I - \alpha \nabla_{\boldsymbol \theta_{i-1}} (\nabla_{\boldsymbol \theta_{i-1}} L_\tau(\boldsymbol \theta_{i-1}))) &= \boldsymbol I - \alpha \nabla_{\boldsymbol \theta_0} \nabla_{\boldsymbol \theta_0} L_\tau\boldsymbol (\theta_0)\\ & = \boldsymbol I - \alpha \boldsymbol H_{A}(\boldsymbol \theta)\\ \end{aligned}\]则
\[\boldsymbol g_{MAML} = \nabla_{\boldsymbol \theta_k} L_{B}(\boldsymbol \theta_k) \cdot (\boldsymbol I - \alpha \boldsymbol H_{A}(\boldsymbol \theta))\]1.5. FOMAML
为了降低二重梯度导致的巨大计算量,作者提出了一种将二重梯度简化计算为一重梯度的方法,即 First-Order MAML (FOMAML)。
FOMAML 假设学习率 $\alpha \rightarrow 0^+$,则前面与 $\alpha$ 相乘的项($k=1$ 时是 Hessian 矩阵,$k>1$ 时是连乘项)因为乘以 $0^+$ 被消去。那么整个 $U_{A}’(\boldsymbol \theta)$ 就等于单位阵了,
此时 FOMAML 的梯度即为
\[\boldsymbol g_{FOMAML} = L'_{B}({}_A\boldsymbol \theta_k)=\nabla_{\boldsymbol \theta_k} L_{B}({}_A\boldsymbol \theta_k)\]也即仅用最后一次更新的模型参数 $_{A}\boldsymbol \theta_k$ 计算梯度。
那么,进行 $k=1$ 次梯度算子更新的 FOMAML 的实现过程就很简单了:
- 采样任务 $\tau$;
- 计算在数据集 A 上的梯度因子 $U^{k=1}_{A}(\boldsymbol \theta)= _{A} \boldsymbol \theta_1 = \phi$;
- 计算在数据集 B 上的损失函数 $L_{B}$ 对 $\phi$ 的(偏)导数:$g_{FOMAML}=\nabla_{\phi} L_{B}(\phi)$;
- 将 $g_{FOMAML}$ 插入外循环更新参数。
简化后的 FOMAML 模型参数更新式为:
\[\begin{aligned} \theta_i' \leftarrow \theta - \alpha \nabla_\theta L_{Ai}(\theta)\\ \theta \leftarrow \theta - \beta \nabla_{\theta'} \sum L_B(\theta')\\ \end{aligned}\]可以看出只需要计算一重梯度即可,作者在文中号称约节省了33%的计算量。
This approximation removes the need for computing Hessian-vector products in an additional backward pass, which we found led to roughly 33% speed-up in network computation.
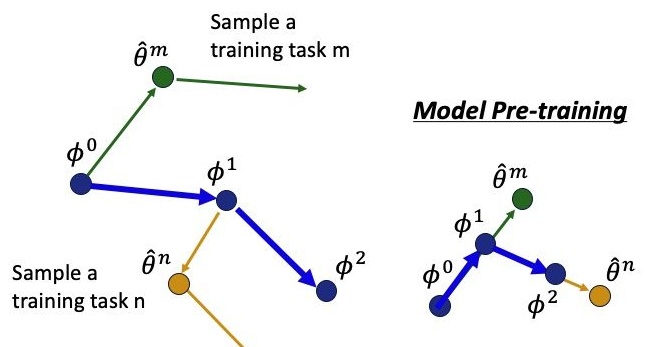
一阶近似的MAML可以看作是如下形式的参数更新:假设每个batch只有一个task,某次采用第m个task来更新模型参数,得到$\hat\theta^m$,再求一次梯度,沿着该梯度方向更新模型的原始参数$\phi$,将其从 $\phi^0$ 更新至 $\phi^1$,以此类推。
与之相比,右边是模型预训练方法,它是将参数根据每次的训练任务一阶导数的方向来更新参数。
1.6. 缺点
MAML的缺点[2]:
-
Hard to train:paper中给出的backbone是4层的conv加1层linear,试想,如果我们换成16层的VGG,每个task在算fast parameter的时候需要计算的Hessian矩阵将会变得非常大。那么你每一次迭代就需要很久,想要最后的model收敛就要更久。
-
Robustness一般:不是说MAML的robustness不好,因为也是由一阶online的优化方法SGD求解出来的,会相对找到一个flatten minima location。然而这和非gradient-based meta learning方法求解出来的model的robust肯定是没法比的。
2. 各类实现
dragen-1860 的 Pytorch 实现:https://github.com/dragen1860/MAML-Pytorch
Tensorflow实现:https://github.com/dragen1860/MAML-TensorFlow
3. 参考文献
[1] Rust-in. MAML 论文及代码阅读笔记.
[2] 人工智障. MAML算法,model-agnostic metalearnings?
[3] Veagau. 【笔记】Reptile-一阶元学习算法
[4] pure water. Reptile原理以及代码详解
[5] Tianhao Wei翻译自Lilian.元学习:学习如何学习【译】