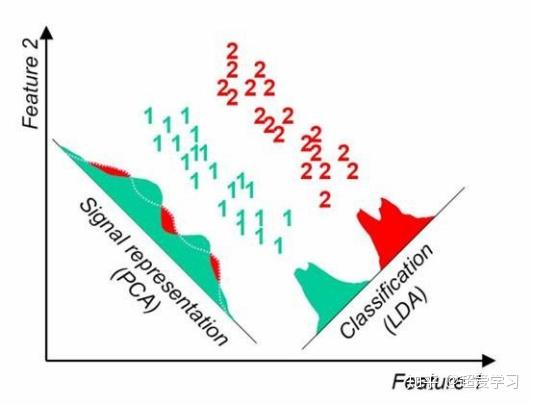
本文介绍了模式识别种常用的两种特征选择与特征降维方法,即线性判别分析(Linear Discriminant Analysis,LDA)和主成分分析(Principal Component Analysis,PCA)。
1. 特征降维
机器学习的很多算法复杂度和数据的维数有着密切关系,甚至与维数呈指数级关联。当数据的特征维度达到成千上万甚至几十万的规模时,机器学习的资源消耗是不可接受的,且有很多特征可能与要解决的分类问题关系不大,因此就会对数据采取降维的操作。
降维就意味着信息的丢失,因为原本每个特征理论上都可以反映出原始数据的某些特质。但鉴于实际数据的特征之间本身常常存在相关性,所以在降维时可以采取一些办法降低信息的损失。
特征降维有两种方法:
- 特征选择:从已有特征向量中选择出若干维度的特征组成新的特征向量,新特征向量的维度一般远小于原始特征向量;
- 特征提取:将原始特征向量经过某种数学变换得到新的特征向量,新特征向量的维度一般远小于原始特征向量;
2. 线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis,LDA)是一种监督学习的降维技术,主要用于数据预处理中的降维、分类任务。LDA的目标是最大化类间区分度的坐标轴成分,将特征空间投影到一个维度更小的 $k$ 维子空间中,同时保持区分类别的信息。简而言之,LDA投影后的数据类内方差最小,类间方差最大。
2.1. Fisher 投影准则
参考前述线性分类器中的 Fisher投影准则 介绍。
2.2. 瑞利商与广义瑞利商
定义瑞利商为
\[R(A,x)=\frac{x^HAx}{x^Hx}\]其中 $x$ 是非零向量,$A\in R^{n\times n}$ 是 Hermitan 矩阵(自共轭矩阵,矩阵中每一个第$i$行第$j$列元素都与第$j$行第$i$列元素共轭相等)。
性质:瑞利商的最大值等于矩阵 $A$ 最大的特征值,最小值等于矩阵 $A$ 的最小特征值。即
\[\lambda_{min} < R(A,x) < \lambda_{max}\]定义广义瑞利商为
\[R(A,x)=\frac{x^HAx}{x^HBx}\]其中 $B$ 为正定矩阵,其他定义同瑞利商。
性质:广义瑞利商的最大值为矩阵 $B^{-\frac{1}{2}}AB^{-\frac{1}{2}}$ 或者说 是矩阵 $B^{-1}A$的最大特征值,最小值是其最小特征值。
2.3. 二分类 LDA
参考前述线性分类器中的 Fisher 投影准则介绍,类间离散度矩阵为
\[\boldsymbol{S}_b = (\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)^\top\]为两向量的外积,其秩为1。
- 一个向量可以看做一个$n\times 1$ 矩阵或者 $1\times n$ 的矩阵,而一个矩阵 $A$ 的秩 $R(A)\leq \min(n,m)$,其中 $n$ 和 $m$ 是这个矩阵的行数和列数,所以单个向量的秩是1;
- 两向量外积也就是一个 $n\times 1$ 矩阵和一个 $1\times n$ 矩阵的积,又两矩阵的积的秩小于等于两者中秩最小的矩阵的秩,也就是 $R(AB)\leq \min(R(A),R(B))$,这里 $R(A)=R(B)=1$,所以 $R(AB)\leq 1$,即两向量外积的秩至多是1。
类内离散度矩阵为
\[\boldsymbol{S}_w = \sum_{i=1}^2 \boldsymbol{S}_{wi}=\sum_{i=1}^2 \sum_{x\in w_i}(x-\mu_i)(x-\mu_i)^\top\]二分类LDA的优化目标函数可以写成
\[\max_{\boldsymbol{w}} J(\boldsymbol{w}) = \frac{\boldsymbol{w}^\top\boldsymbol{S}_b\boldsymbol{w}}{\boldsymbol{w}^\top\boldsymbol{S}_w\boldsymbol{w}}\]目标是求使得 $J(\boldsymbol{w})$ 最大的投影方向 $\boldsymbol{w}$。
根据前述 Fisher投影准则 的推导,上述优化问题最终可转化为求矩阵 $\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$ 的特征值 $\lambda$ 和特征向量 $\boldsymbol{w}^{\star}$。
这里给出另外一种推导思路,上述目标函数正好是广义瑞利商的形式,因此其最大值为 $\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$ 的最大特征值,那么投影方向 $\boldsymbol{w}$ 即为 $\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$ 对应特征值 $\lambda$ 的特征向量。
若 $\boldsymbol{S}_w$ 不可逆,可进行如下操作进行松弛
\[\boldsymbol{S}_w = \boldsymbol{S}_w + \beta \boldsymbol{I}\]其中 $\beta$ 是一个很小的数。
实际使用时为得到数值解的稳定性,通常对 $\boldsymbol{S}_w$ 进行奇异值分解得到 $\boldsymbol{S}_w^{-1}$
\[\boldsymbol{S}_w=\boldsymbol{U}\Sigma \boldsymbol{V}^\top \Rightarrow \boldsymbol{S}_w^{-1} = \boldsymbol{V}\Sigma \boldsymbol{U}^\top\]2.4. 多分类 LDA
假设为 $C$ 分类,类内离散度矩阵定义保持不变,可直接扩展至 $C$ 类的情况,有
\[\boldsymbol{S}_w = \sum_{i=1}^C \boldsymbol{S}_{wi}=\sum_{i=1}^C \sum_{\boldsymbol{x}\in w_i}(\boldsymbol{x}-\boldsymbol{\mu}_i)(\boldsymbol{x}-\boldsymbol{\mu}_i)^\top\]对于类间离散度矩阵,无法像之前二分类那样定义(即 $\boldsymbol{S}_b=(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)^\top$,度量两类均值的散列情况),需要改为度量每类均值点相对于样本中心的散列情况,即
\[\boldsymbol{S}_b= \sum_{i=1}^C N_i(\boldsymbol{\mu}_i-\boldsymbol{\mu})(\boldsymbol{\mu}_i-\boldsymbol{\mu})^\top\]类似于将 $\boldsymbol{\mu}_i$ 看作样本点,$\boldsymbol{\mu}$ 是均值的协方差矩阵,唯一的差别是多了一个权重系数。如果某类里面的样本点较多,那么其权重稍大,权重用 $N_i/N$ 表示,但由于 $J(\boldsymbol{w})$对倍数不敏感,因此使用 $N_i$ 即可。
注意到,$\boldsymbol{S}_b$ 是 $C$ 个秩为 1 的向量外积得到的矩阵求和,因此 $\boldsymbol{S}_b$ 的秩不会超过 $C$。因此 LDA 最终只能得到 $C$ 个不为零的特征向量。
矩阵的秩小于等于各个相加矩阵的秩的和,即 $R(A+B)\leq R(A)+R(B)$
又因为,各个类别的均值与总样本均值之间线性相关,即
\[\boldsymbol{\mu} = \frac{1}{N} \sum_{\forall \boldsymbol{x}}\boldsymbol{x} = \frac{1}{N}\sum_{\boldsymbol{x}\in w_i} N_i\boldsymbol{\mu}_i\]知道了前 $C-1$ 个 $(\boldsymbol{\mu}_i-\boldsymbol{\mu})$ 后,最后一个 $(\boldsymbol{\mu}_C-\boldsymbol{\mu})$ 可以有前面的 $\boldsymbol{\mu}_i$ 来线性表示,因此$\boldsymbol{S}_b$ 的秩为 $C-1$。
所以在计算特征向量矩阵(类内散度矩阵 $\boldsymbol{S}_w$ 的逆 $\times$ 类间散度矩阵 $\boldsymbol{S}_b$)时,可以发现只有 $C-1$ 个特征值不为零的特征向量。因此,LDA 最多将特征维度降低到 $C-1$ 维。
假设样本原始特征维度为 $k$,前 $d=C-1$ 个最大特征值对应的特征向量组成的投影矩阵为 $\boldsymbol{W}=[\boldsymbol{w}1, \boldsymbol{w}_2,\cdots, \boldsymbol{w}{d}]\in \mathbb{R}^{k\times d}$,那么多分类 LDA 的优化目标函数为
\[\max_{\boldsymbol{W}} J(\boldsymbol{W}) = \frac{\boldsymbol{W}^\top\boldsymbol{S}_b\boldsymbol{W}}{\boldsymbol{W}^\top\boldsymbol{S}_w\boldsymbol{W}}\]最终可将 $k$ 维高维特征降维至 $d$ 维
\[\boldsymbol{z} = \boldsymbol{W}\boldsymbol{x}\]2.5. LDA 的特点
LDA 是一个有监督的方法,具有如下特点:
- 根据原始数据样本的均值进行分类
- 不同类数据拥有相近的协方差矩阵
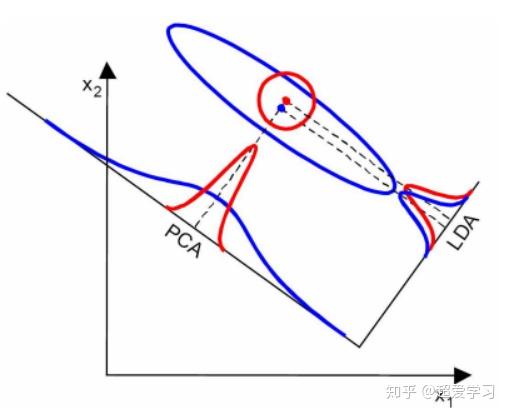
当然,在实际情况中,不可能满足以上两个假设。但是当数据主要是由均值来区分的时候,LDA一般都可以取得很好的效果。见下面两个对比图。
上图中,两类数据的均值差异较大,但协方差矩阵十分接近,因此 LDA 分类效果好于 PCA。
上图中,两类数据的均值差异很小,但协方差矩阵相差十分明显,因此 LDA 分类效果差于 PCA。
LDA 的优点:
- 计算速度快
- 充分利用了先验知识
LDA 的缺点:
- 不适合对非高斯分布的样本降维
- 降维之后的维数最多为类别数-1,所以当数据维度很高,但是类别数少的时候,算法并不适用
- 可能会过度拟合数据
3. 主成分分析(PCA)
主成分分析(Principal Component Analysis,PCA)是常用的特征提取数据分析方法。PCA是通过线性变换,将原始数据变换为一组各维度线性无关的数据表示方法,可用于提取数据的主要特征分量,常用于高维数据的降维。
为了最大限度保留对原始数据的解释,一般会用最大方差理论或最小损失理论,使得第一主成分有着最大的方差或变异数 (就是说其能尽量多的解释原始数据的差异);随后的每一个主成分都与前面的主成分正交,且有着仅次于前一主成分的最大方差 (正交简单的理解就是两个主成分空间夹角为90°,两者之间无线性关联,从而完成去冗余操作)。
PCA 降维的原理在于,大部分方差集中在前 $k$ 个坐标轴,后续坐标轴方差接近 0,因此可忽略后者,仅保留前 $k$ 个坐标轴。这相当于保留主要特征维度,忽略方差接近 0 的特征,实现数据降维。
3.1. 数学推导
PCA 的推导思路在于,对于正交属性空间中的样本点,如何用一个超平面对所有样本进行恰当的表达?核心在于以下两点:
- 最近重构性:样本点到这个超平面的距离都足够近,也即投影前后所有样本点的总距离最小。
- 最大可分性:样本点在这个超平面上的投影尽可能分开,也即投影后的样本点方差最大。
基于最近重构性和最大可分性,能分别得到PCA的两种等价推导,下面分别展开说明。
3.1.1. 最近重构性(K-L变换)
首先对 $n$ 个 $d$ 维样本进行中心化,即将所有样本变换为均值为 0,也即
\[\sum_{i=1}^n \boldsymbol{x}_i=0,\quad \boldsymbol{x}_i\in\mathbb{R}^{d},\; i=1,2,\cdots,n\]- 单个样本的角度
目标是找到投影矩阵 $\boldsymbol{W}\in\mathbb{R}^{d\times k}$,将样本投影到低维空间
\[\boldsymbol{z}_i = \boldsymbol{W}^\top\boldsymbol{x}_i\quad \in\mathbb{R}^k\]再重构回原始空间
\[\hat{\boldsymbol{x}}_i=\boldsymbol{W}\boldsymbol{z}_i=\boldsymbol{W}\boldsymbol{W}^\top\boldsymbol{x}_i\quad \in\mathbb{R}^d\]对所有 $n$ 个样本均进行投影后,用重构前后的均方误差衡量重构误差,有
\[J(\boldsymbol{W}) = \sum_{i=1}^n\Vert \boldsymbol{x}_i - \hat{\boldsymbol{x}}_i \Vert^2 = \sum_{i=1}^n\Vert \boldsymbol{x}_i - \boldsymbol{W}\boldsymbol{W}^\top\boldsymbol{x}_i \Vert^2\]- 样本矩阵的角度
令样本矩阵(每一行是一个样本)为
\[\boldsymbol{X}=\begin{bmatrix} \boldsymbol{x}_1^\top\\ \boldsymbol{x}_2^\top\\ \vdots\\ \boldsymbol{x}_n^\top \end{bmatrix}\]则投影后的低维样本矩阵为
\[\boldsymbol{Z}=\boldsymbol{X}\boldsymbol{W}\quad \in\mathbb{R}^{n\times k}\]重构后的样本矩阵为
\[\hat{\boldsymbol{X}}=\boldsymbol{Z}\boldsymbol{W}^\top=\boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top\quad \in\mathbb{R}^{n\times d}\]将上述误差 $J(\boldsymbol{W})$ 按照矩阵逐元素展开写,有
\[J(\boldsymbol{W}) = \sum_{i=1}^n\sum_{j=1}^d\left(x_{ij} - \left[\boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top\right]_{ij}\right)^2\]注意到,上式就是矩阵的 Frobenius 范数的平方形式,即
\[J(\boldsymbol{W}) = \Vert\boldsymbol{X} - \boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top\Vert_F^2\]根据矩阵的 Frobenius 范数的性质,有
\[\Vert\boldsymbol{A}\Vert_F = \sqrt{\sum_{i=1}^m\sum_{j=1}^n \boldsymbol{A}_{ij}^2} = \sqrt{\text{tr}(\boldsymbol{A}^\top \boldsymbol{A})}\]\[\begin{aligned} \Vert\boldsymbol{X} - \boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top\Vert_F^2 &= \text{tr}\left( (\boldsymbol{X} - \boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top)^\top(\boldsymbol{X} - \boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top) \right)\\ &= \text{tr}(\boldsymbol{X}^\top\boldsymbol{X}) - 2\text{tr}(\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top) + \text{tr}(\boldsymbol{W}\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W}\boldsymbol{W}^\top)\\ &= \text{tr}(\boldsymbol{X}^\top\boldsymbol{X}) - \text{tr}(\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W}) \end{aligned}\]
其中第二行展开是因为迹是线性算子,可以保证分配律。第三行展开利用了正交投影矩阵的性质和迹的循环置换性。
正交投影矩阵:$\boldsymbol{W}\boldsymbol{W}^\top = \boldsymbol{I}$
迹的循环置换性:$\text{tr}(\boldsymbol{A}\boldsymbol{B}\boldsymbol{C}) = \text{tr}(\boldsymbol{B}\boldsymbol{C}\boldsymbol{A}) = \text{tr}(\boldsymbol{C}\boldsymbol{A}\boldsymbol{B})$
注意到,$\boldsymbol{X}^\top\boldsymbol{X}$ 是样本的协方差矩阵,对优化问题而言是常数,不影响优化结果,因此最近重构性推导的优化问题可描述为
\[\begin{aligned} \min_{\boldsymbol{W}} &\quad -\text{tr}(\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W}) \\ s.t. &\quad \boldsymbol{W}^\top\boldsymbol{W}=\boldsymbol{I} \end{aligned}\]3.1.2. 最大可分性
要让投影后所有样本点能尽可能分开,则投影后样本点方差最大。
同样首先对 $n$ 个 $d$ 维样本进行中心化,假设中心化后样本矩阵为 $\boldsymbol{X}\in\mathbb{R}^{n\times d}$,即
\[\boldsymbol{X}=\begin{bmatrix} \boldsymbol{x}_1^\top\\ \boldsymbol{x}_2^\top\\ \vdots\\ \boldsymbol{x}_n^\top \end{bmatrix}\]协方差矩阵为 $\boldsymbol{X}^\top\boldsymbol{X}$。给定某个投影方向 $\boldsymbol{w}$ 满足 $\Vert\boldsymbol{w}\Vert_2=1$,则投影后使样本方差最大等价于
\[\max_{\boldsymbol{w}} \quad Var(\boldsymbol{X}\boldsymbol{w}) = \boldsymbol{w}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{w}\]推广到 $k$ 个主成分(正交方向),投影矩阵 $\boldsymbol{W}\in\mathbb{R}^{d\times k}$ 满足 $\boldsymbol{W}^\top\boldsymbol{W}=\boldsymbol{I}$,优化目标为
\[\max_{\boldsymbol{w}_i} \quad \sum_{i=1}^k\boldsymbol{w}_i^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{w}_i\]注意到上式改写为矩阵后就是矩阵的对角元素(迹),则目标函数可改写为
\[\max_{\boldsymbol{W}} \quad \text{tr}(\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W})\]等价于求解如下优化问题
\[\begin{aligned} \max_{\boldsymbol{W}} &\quad \text{tr}(\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W})\\ s.t. &\quad \boldsymbol{W}^\top\boldsymbol{W}=\boldsymbol{I} \end{aligned}\]可以发现和最近重构性等价。
3.1.3. 拉格朗日乘子法求解
对于最近重构性,最小化目标函数,拉格朗日乘子项使用正号
\[J(\boldsymbol{W}) = -\text{tr}(\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W})+\Lambda^\top(\boldsymbol{W}^\top\boldsymbol{W}-\boldsymbol{I})\]对于最大可分性,最大化目标函数,拉格朗日乘子项使用负号
\[J(\boldsymbol{W}) = \text{tr}(\boldsymbol{W}^\top\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W})-\Lambda^\top(\boldsymbol{W}^\top\boldsymbol{W}-\boldsymbol{I})\]二者等价。对上式求导(注意第一项利用迹的微分公式),令导数等于零,整理有
\[\boldsymbol{X}^\top\boldsymbol{X}\boldsymbol{W} = \Lambda \boldsymbol{W}\]该方程是特征值问题的形式,$\boldsymbol{W}$ 是协方差矩阵 $\boldsymbol{X}^\top\boldsymbol{X}$ 最大的 $d$ 个特征值对应的特征向量组成。$\Lambda$ 是对角线元素为协方差矩阵特征值的对角矩阵。根据 $\boldsymbol{z}_i=\boldsymbol{W}^\top\boldsymbol{x}_i$ 即可将特征降维。
在信号处理领域,从最近重构性出发的推导过程被称为 K-L变换,用于离散信号的去相关的线性变换。从数学上看,K-L变换和PCA的核心步骤是相同的:都是对协方差矩阵进行特征值分解,然后选择最大的特征值对应的特征向量作为投影方向。K-L变换更偏向于信号处理领域,强调信号的能量集中特性,适用于随机信号的降维和压缩。PCA更偏向于统计学和机器学习领域,强调数据的方差解释能力,适用于数据的降维和可视化。两者在数学上是等价的,但在应用背景和解释方式上有所不同。
3.2. 算法流程
首先将 $n$ 个 $d$ 维数据排列成 $d$ 行 $n$ 列矩阵的形式,即每一列是一个样本数据。注意,为了方便从另一个角度推导,这里和前面算法优化问题推导时使用的样本矩阵定义不同,存在一个转置,最终不影响求解结果。
\[\boldsymbol{X} = [\boldsymbol{x}_1, \boldsymbol{x}_2,\cdots, \boldsymbol{x}_n] \in \mathbb{R}^{d\times n}\]然后对数据进行中心化,即计算所有数据的均值后,将所有数据减去均值
\[\begin{aligned} \bar{\boldsymbol{X}}&=[\boldsymbol{x}_1-\boldsymbol{\mu}, \boldsymbol{x}_2-\boldsymbol{\mu},\cdots, \boldsymbol{x}_n-\boldsymbol{\mu}]\\ &=[\bar{\boldsymbol{x}}_1, \bar{\boldsymbol{x}}_2,\cdots, \bar{\boldsymbol{x}}_n]\\ &=\begin{bmatrix} \bar x^1_1 & \bar x^2_1 & \cdots & \bar x^n_1\\ \bar x^1_2 & \bar x^2_2 & \cdots & \bar x^n_2\\ \vdots & \vdots & \ddots & \vdots \\ \bar x^1_d & \bar x^2_d & \cdots & \bar x^n_d\\ \end{bmatrix} \end{aligned}\]此时满足
\[\sum_{i=0}^m \bar{\boldsymbol{x}}_i = 0\]然后计算这个矩阵的协方差矩阵,即
\[\begin{aligned} \boldsymbol{\Sigma} &= \frac{1}{n}\bar{\boldsymbol{X}}\bar{\boldsymbol{X}}^\top \in \mathbb{R}^{d \times d}\\ &=\frac{1}{n} \begin{bmatrix} \sum_{i=1}^n (\bar x^i_1)^2 & \sum_{i=1}^n \bar x^i_1\cdot \bar x^i_2 & \cdots & \sum_{i=1}^n \bar x^i_1\cdot \bar x^i_d\\ \sum_{i=1}^n \bar x^i_2\cdot \bar x^i_1 & \sum_{i=1}^n (\bar x^i_2)^2 & \cdots & \sum_{i=1}^n \bar x^i_2\cdot \bar x^i_d\\ \vdots & \vdots & \ddots & \vdots \\ \sum_{i=1}^n \bar x^i_d\cdot \bar x^i_1 & \sum_{i=1}^n \bar x^i_d\cdot \bar x^i_2 & \cdots & \sum_{i=1}^n (\bar x^i_d)^2\\ \end{bmatrix} \end{aligned}\]其中,对角线上的元素为各个随机变量(特征)的方差,非对角线上的元素为两两随机变量之间的协方差。
求出协方差矩阵的特征值 $\lambda_i$ 和对应的正交化单位特征向量 $\boldsymbol{w}_i$。
将特征向量按照对应特征值从大到小,自上而下按行排列成矩阵,取前 $k$ 行组成矩阵 $\boldsymbol{W}$。
$\boldsymbol{Z} = \boldsymbol{W}\boldsymbol{X}$ 即为降维到 $k$ 维后的数据。(如果按列排列特征向量,则 $\boldsymbol{W}$ 取转置)
3.3. PCA 的特点
根据上面对PCA的数学原理的解释,可以了解到一些PCA的能力和限制。PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。
因此,PCA也存在一些限制,例如它可以很好的解除线性相关,但是对于高阶相关性就没有办法了,对于存在高阶相关性的数据,可以考虑Kernel PCA,通过Kernel函数将非线性相关转为线性相关。另外,PCA假设数据各主特征是分布在正交方向上,如果在非正交方向上存在几个方差较大的方向,PCA的效果就大打折扣了。
最后需要说明的是,PCA是一种无参数技术,也就是说面对同样的数据,如果不考虑清洗,谁来做结果都一样,没有主观参数的介入,所以PCA便于通用实现,但是本身无法个性化的优化。